Learning Outcomes
- Add or subtract fractions
- Multiply fractions
- Divide fractions
Probabilities are often stated as fractions. Sometimes we are interested in probabilities involving several events. The methods used to calculate these probabilities will require addition, subtraction, multiplication and division. This section will remind you how to do these operations on fractions. As you work through the rest of the course, you can return this section as needed for a quick reminder of operations on fractions.
Add Fractions
When you need to add or subtract fractions, you will need to first make sure that the fractions have the same denominator. The denominator tells you how many pieces the whole has been broken into, and the numerator tells you how many of those pieces you are using.
Suppose a pizza has been cut into 4 equal slices, and one slice of a pizza has been eaten leaving 3 slices. The fraction [latex]\frac{3}{4}[/latex] represents how much of a whole pizza we have left.

Suppose you have another pizza that had been cut into 8 equal parts and 3 of those parts were gone, leaving [latex]\frac{5}{8}[/latex]. To describe the total amount of pizza remaining as a single fraction, we need a common denominator. The lowest common denominator is the least common multiple (LCM) of the two original denominators. Finding the least common multiple of a list of numbers using prime factorizations was described in a previous section. See the example below for a demonstration of our pizza problem.
Example
One pizza, cut into four slices, has one missing. Another pizza of the same size has been cut into eight pieces, of which three have been removed. Describe the total amount of pizza left in the two pizzas using common terms.
Example
Add [latex]\frac{5}{12}+\frac{1}{12}[/latex]. Simplify the answer.
To add fractions with unlike denominators, first rewrite them with like denominators. Then add or subtract the numerators over the common denominator.
Adding Fractions with Unlike Denominators
- Find a common denominator.
- Rewrite each fraction as an equivalent fraction using the common denominator.
- Now that the fractions have a common denominator, you can add the numerators.
- Simplify by canceling out all common factors in the numerator and denominator.
In the next example you are shown how to add two fractions with different denominators, then simplify the answer.
Example
Add [latex]\frac{1}{3}+\frac{1}{2}[/latex]. Simplify the answer.
While any common multiple of the two denominators can be used, the least common multiple is the easiest.
In the following video you will see an example of how to add two fractions with different denominators.
Try It
Subtract Fractions
Subtracting fractions follows the same technique as adding them. First, determine whether or not the denominators are alike. If not, rewrite each fraction as an equivalent fraction, all having the same denominator. Below are some examples of subtracting fractions whose denominators are not alike.
Example
Subtract [latex]\frac{5}{6} - \frac{2}{9}[/latex]. Simplify the answer.
We can perform additions and subtractions on three or more fractions, as seen in the example below.
Example
Subtract [latex]\frac{1}{6} + \frac{1}{4} - \frac{1}{12}[/latex]. Simplify the answer.
Try It
In the following video you will see an example of how to subtract fractions with unlike denominators.
Multiply Fractions
When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have [latex]\Large\frac{3}{4}[/latex] of a candy bar and you want to find [latex]\Large\frac{1}{2}[/latex] of the [latex]\Large\frac{3}{4}[/latex]:
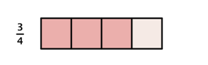
By dividing each fourth in half, you can divide the candy bar into eighths.

Then, choose half of those to get [latex]\Large\frac{3}{8}[/latex].

In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
Multiplying Two Fractions
[latex]\Large\frac{a}{b}\cdot\Large\frac{c}{d}=\Large\frac{a\cdot c}{b\cdot d}=\Large\frac{\text{product of the numerators}}{\text{product of the denominators}}[/latex]
Example
Multiply [latex]\Large\frac{2}{3}\cdot\Large\frac{4}{5}[/latex]
If a fraction has common factors in the numerator and denominator, we can reduce the fraction to its simplified form by removing the common factors.
Example
Multiply [latex]\Large\frac{2}{3}\cdot\Large\frac{3}{8}[/latex]
You can simplify first, before you multiply two fractions, to make your work easier. This allows you to work with smaller numbers when you multiply.
Try It
In the following video you will see an example of how to multiply two fractions, then simplify the answer.
Divide Fractions
There are times when you need to use division to solve a problem. For example, if painting one coat of paint on the walls of a room requires [latex]3[/latex] quarts of paint and you have a bucket that contains [latex]6[/latex] quarts of paint, how many coats of paint can you paint on the walls? You divide [latex]6[/latex] by [latex]3[/latex] for an answer of [latex]2[/latex] coats. There will also be times when you need to divide by a fraction. Suppose painting a closet with one coat only required [latex]\Large\frac{1}{2}[/latex] quart of paint. How many coats could be painted with the 6 quarts of paint? To find the answer, you need to divide [latex]2[/latex] by the fraction, [latex]\Large\frac{1}{2}[/latex].
Before we begin dividing fractions, let’s cover some important terminology.
- reciprocal: two fractions are reciprocals if their product is [latex]1[/latex] (Don’t worry; we will show you examples of what this means.)
Note that for [latex]a \neq 0[/latex] and [latex]b \neq 0[/latex], [latex]\frac{a}{b} \cdot \frac{b}{a} = \frac{a \cdot b}{b \cdot a} = \frac{a \cdot b}{a \cdot b} = 1[/latex]. The reciprocal of a fraction can be found by interchanging the numerator and denominator.
The reciprocal of [latex]\frac{a}{b}[/latex] is [latex]\frac{b}{a}[/latex].
Dividing fractions requires using the reciprocal of a number or fraction. Here are some examples of reciprocals:
| Original number | Reciprocal |
|---|---|
| [latex]\Large\frac{3}{4}[/latex] | [latex]\Large\frac{4}{3}[/latex] |
| [latex]\Large\frac{1}{2}[/latex] | [latex]\Large\frac{2}{1}[/latex] |
| [latex]3=\Large\frac{3}{1}[/latex] | [latex]\Large\frac{1}{3}[/latex] |
| [latex]2\Large\frac{1}{3}=\Large\frac{7}{3}[/latex] | [latex]\Large\frac{3}{7}[/latex] |
 Caution! Division by zero is undefined and so is the reciprocal of any fraction that has a zero in the numerator. For any real number a, [latex]\Large\frac{a}{0}[/latex] is undefined. Additionally, the reciprocal of [latex]\Large\frac{0}{a}[/latex] will always be undefined.
Caution! Division by zero is undefined and so is the reciprocal of any fraction that has a zero in the numerator. For any real number a, [latex]\Large\frac{a}{0}[/latex] is undefined. Additionally, the reciprocal of [latex]\Large\frac{0}{a}[/latex] will always be undefined.Dividing is Multiplying by the Reciprocal
For all division, you can turn the operation into multiplication by using the reciprocal. Dividing is the same as multiplying by the reciprocal.
Look at the diagram of two pizzas below. How can you divide what is left (the red shaded region) among [latex]6[/latex] people fairly?
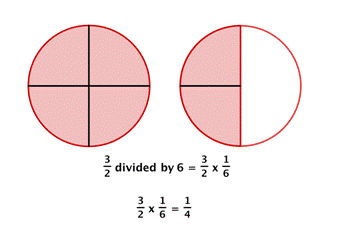
Each person gets one piece, so each person gets [latex]\Large\frac{1}{4}[/latex] of a pizza.
Dividing a fraction by a whole number is the same as multiplying by the reciprocal, so you can always use multiplication of fractions to solve division problems.
Example
Find [latex]\Large\frac{2}{3}\div \normalsize 4[/latex]
Example
Divide. [latex]9\div\Large\frac{1}{2}[/latex]
Divide a Fraction by a Fraction
Sometimes you need to solve a problem that requires dividing by a fraction. Suppose you have a pizza that is already cut into [latex]4[/latex] slices. How many [latex]\Large\frac{1}{2}[/latex] slices are there?
 |
 |
There are [latex]8[/latex] slices. You can see that dividing [latex]4[/latex] by [latex]\Large\frac{1}{2}[/latex] gives the same result as multiplying [latex]4[/latex] by [latex]2[/latex].
What would happen if you needed to divide each slice into thirds?
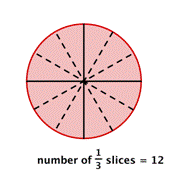
You would have [latex]12[/latex] slices, which is the same as multiplying [latex]4[/latex] by [latex]3[/latex].
Dividing with Fractions
- Find the reciprocal of the number that follows the division symbol.
- Multiply the first number (the one before the division symbol) by the reciprocal of the second number (the one after the division symbol).
Any easy way to remember how to divide fractions is the phrase “keep, change, flip.” This means to KEEP the first number, CHANGE the division sign to multiplication, and then FLIP (use the reciprocal) of the second number.
Example
Divide [latex]\Large\frac{2}{3}\div\Large\frac{1}{6}[/latex]
Example
Divide [latex]\Large\frac{3}{5}\div\Large\frac{2}{3}[/latex]
When solving a division problem by multiplying by the reciprocal, remember to write all whole numbers and mixed numbers as improper fractions. The final answer should be simplified and written as a mixed number.
Try It
In the following video you will see an example of how to divide an integer by a fraction, as well as an example of how to divide a fraction by another fraction.
Candela Citations
- Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaption. License: CC BY: Attribution
- Question ID: 624, 629, 533, 558. Authored by: Lippman, D. Provided by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Unit 2: Fractions and Mixed Numbers, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Ex: Add Fractions with Unlike Denominators (Basic with Model). Authored by: James Sousa (Mathispower4u). Located at: https://youtu.be/zV4q7j1-89I. License: CC BY: Attribution
- Ex 1: Multiply Fractions (Basic). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/f_L-EFC8Z7c. License: CC BY: Attribution
- Ex 1: Diviide Fractions (Basic). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/F5YSNLel3n8. License: CC BY: Attribution
