Slope-Intercept Form for the Equation of a Line

Learning Outcomes

  • Use slope-intercept form to plot equations of lines
  • Interpret the slope and y-intercept for the equation of a line

Slope-Intercept Form

Perhaps the most familiar form of a linear equation is slope-intercept form written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.

The Slope of a Line

The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.

[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

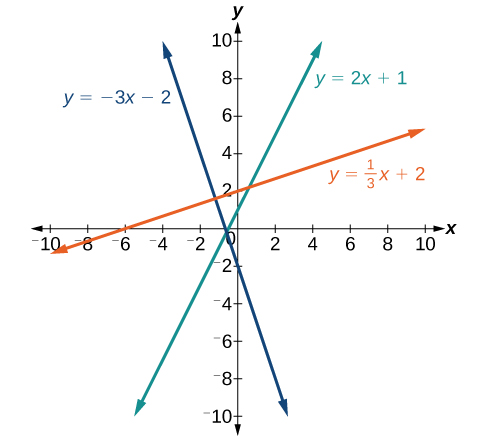
If the slope is positive, the line slants upward to the right. If the slope is negative, the line slants downward to the right. As the slope increases, the line becomes steeper. Some examples are shown below. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].

Coordinate plane with the x and y axes ranging from negative 10 to 10. Three linear functions are plotted: y = negative 3 times x minus 2; y = 2 times x plus 1; and y = x over 3 plus 2.

A General Note: The Slope of a Line

The slope of a line, m, represents the change in y over the change in x. Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:

[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Example: Finding the Slope of a Line Given Two Points

Find the slope of a line that passes through the points [latex]\left(2,-1\right)[/latex] and [latex]\left(-5,3\right)[/latex].

Try It

Example: Identifying the Slope and y-intercept of a Line Given an Equation

Identify the slope and y-intercept given the equation [latex]y=-\frac{3}{4}x - 4[/latex].

INTERPRETING THE SLOPE AND Y-INTERCEPT

The y-intercept, b, is the point where the line crosses the y-axis. The y-intercept also tells us the value of y when [latex]x = 0[/latex].

The slope, m, is the change in y divided by the change in x. Then if x increases by 1 unit, y changes by m units.

Example: Identifying the Slope and y-intercept of a Line Given an Equation

A restaurant charges $200 to rent a private dining room and $15 per person for a luncheon. Then the cost y, in dollars, if x persons attend the luncheon is described by

[latex]y=15x+200[/latex].

The line is in slope-intercept form, [latex]y=mx+b[/latex], the given line has a slope of [latex]m=15[/latex], and the y-intercept is [latex]b=200[/latex]. The y-intercept tells us that the restaurant will charge $200 even if no one attends the luncheon. The slope, 15, tells us the cost will increase by $15 for every additional guest at the luncheon.

Example: Identifying the Slope and y-intercept of a Line Given an Equation

A student begins driving home for a holiday break. The distance, y, from home after x hours of driving is described by

[latex]y=-45x+150[/latex].

The line is in slope-intercept form, [latex]y=mx+b[/latex], the given line has a slope of [latex]m=-45[/latex], and the y-intercept is [latex]b=150[/latex]. The y-intercept tells us that when the student begins their trip, they are 150 miles from home. The slope, -45, tells us the distance from home decreases by 45 miles for every hour the student drives.

Try It