The Empirical Rule

Learning Outcomes

  • Use the empirical rule to determine values at 1, 2, and 3 standard deviations from the mean

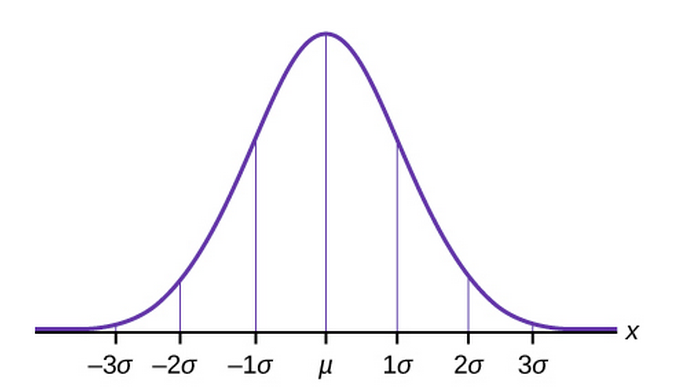
The Empirical Rule

If X is a random variable and has a normal distribution with mean µ and standard deviation σ, then the empirical rule says the following:

  • About 68% of the x values lie between –1σ and +1σ of the mean µ (within one standard deviation of the mean).
  • About 95% of the x values lie between –2σ and +2σ of the mean µ (within two standard deviations of the mean).
  • About 99.7% of the x values lie between –3σ and +3σ of the mean µ(within three standard deviations of the mean). Notice that almost all thex values lie within three standard deviations of the mean.
  • The z-scores for +1σ and –1σ are +1 and –1, respectively.
  • The z-scores for +2σ and –2σ are +2 and –2, respectively.
  • The z-scores for +3σ and –3σ are +3 and –3 respectively.

The empirical rule is also known as the 68-95-99.7 rule.

Graph of the empirical Rule. The graph is a bell curve showing 3 standard deviations from mu in both directions with mu being at the center. The standard deviations are labeled -3 sigma, -2 sigma, -1 sigma, 1 sigma, 2 sigma, and 3 sigma. These are centered around mu.

Example

The mean height of 15 to 18-year-old males from Chile from 2009 to 2010 was 170 cm with a standard deviation of 6.28 cm. Male heights are known to follow a normal distribution. Let X = the height of a 15 to 18-year-old male from Chile in 2009 to 2010. Then X ~ N(170, 6.28).

a. Suppose a 15 to 18-year-old male from Chile was 168 cm tall from 2009 to 2010. The z-score when x = 168 cm is z = _______. This z-score tells you that x = 168 is ________ standard deviations to the ________ (right or left) of the mean _____ (What is the mean?).

b. Suppose that the height of a 15 to 18-year-old male from Chile from 2009 to 2010 has a z-score of z = 1.27. What is the male’s height? The z-score (z = 1.27) tells you that the male’s height is ________ standard deviations to the __________ (right or left) of the mean.

try it

Use the information in the previous Example to answer the following questions.

  1. Suppose a 15 to 18-year-old male from Chile was 176 cm tall from 2009 to 2010. The z-score when x = 176 cm is z = _______. This z-score tells you that x = 176 cm is ________ standard deviations to the ________ (right or left) of the mean _____ (What is the mean?).
  2. Suppose that the height of a 15 to 18-year-old male from Chile from 2009 to 2010 has a z-score of z = –2. What is the male’s height? The z-score (z = –2) tells you that the male’s height is ________ standard deviations to the __________ (right or left) of the mean.

Example

From 1984 to 1985, the mean height of 15 to 18-year-old males from Chile was 172.36 cm, and the standard deviation was 6.34 cm. Let Y = the height of 15 to 18-year-old males from 1984 to 1985. Then Y ~ N(172.36, 6.34).

The mean height of 15 to 18-year-old males from Chile from 2009 to 2010 was 170 cm with a standard deviation of 6.28 cm. Male heights are known to follow a normal distribution. Let X = the height of a 15 to 18-year-old male from Chile in 2009 to 2010. Then X ~ N(170, 6.28).

Find the z-scores for x = 160.58 cm and y = 162.85 cm. Interpret each z-score. What can you say about x = 160.58 cm and y = 162.85 cm?

 

 

try it

In 2012, 1,664,479 students took the SAT exam. The distribution of scores in the verbal section of the SAT had a mean µ = 496 and a standard deviation σ = 114. Let X = a SAT exam verbal section score in 2012. Then X ~ N(496, 114).

Find the z-scores for [latex]x_1= 325[/latex] and [latex]x_2 = 366.21[/latex]. Interpret each z-score. What can you say about [latex]x_1 = 325[/latex] and [latex]x_2 = 366.21[/latex]?

Example

Suppose x has a normal distribution with mean 50 and standard deviation 6.

  • About 68% of the x values lie between –1σ = (–1)(6) = –6 and 1σ = (1)(6) = 6 of the mean 50. The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation of the mean 50. The z-scores are –1 and +1 for 44 and 56, respectively.
  • About 95% of the x values lie between –2σ = (–2)(6) = –12 and 2σ = (2)(6) = 12. The values 50 – 12 = 38 and 50 + 12 = 62 are within two standard deviations of the mean 50. The z-scores are –2 and +2 for 38 and 62, respectively.
  • About 99.7% of the x values lie between –3σ = (–3)(6) = –18 and 3σ= (3)(6) = 18 of the mean 50. The values 50 – 18 = 32 and 50 + 18 = 68 are within three standard deviations of the mean 50. The z-scores are –3 and +3 for 32 and 68, respectively

 

try it

Suppose X has a normal distribution with mean 25 and standard deviation five. Between what values of x do 68% of the values lie?

Example

From 1984 to 1985, the mean height of 15 to 18-year-old males from Chile was 172.36 cm, and the standard deviation was 6.34 cm. Let Y = the height of 15 to 18-year-old males in 1984 to 1985. Then Y ~ N(172.36, 6.34).

  1. About 68% of the y values lie between what two values? These values are ________________. The z-scores are ________________, respectively.
  2. About 95% of the y values lie between what two values? These values are ________________. The z-scores are ________________ respectively.
  3. About 99.7% of the y values lie between what two .7% of the values lie between 153.34 and 191.38. The z-scores are –3 and 3.

try it

The scores on a college entrance exam have an approximate normal distribution with mean, µ = 52 points and a standard deviation, σ = 11 points.

  1. About 68% of the y values lie between what two values? These values are ________________. The z-scores are ________________, respectively.
  2. About 95% of the y values lie between what two values? These values are ________________. The z-scores are ________________, respectively.
  3. About 99.7% of the y values lie between what two values? These values are ________________. The z-scores are ________________, respectively.