Venn Diagram

Learning Outcomes

  • Draw a Venn diagram to represent a given scenario
  • Use a Venn diagram to calculate probabilities

Venn Diagram

A Venn diagram is a picture that represents the outcomes of an experiment. It generally consists of a box that represents the sample space S together with circles or ovals. The circles or ovals represent events.

Example

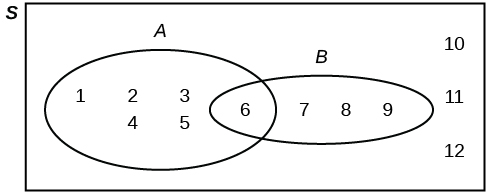
Suppose an experiment has the outcomes [latex]1, 2, 3, ... , 12[/latex] where each outcome has an equal chance of occurring. Let event [latex]A = \{1, 2, 3, 4, 5, 6\}[/latex] and event [latex]B = \{6, 7, 8, 9\}[/latex]. Then [latex]A \text{ AND } B = \{6\}[/latex] and [latex]A \text{ OR }B = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}[/latex]. The Venn diagram is as follows:

A Venn diagram. An oval representing set A contains the values 1, 2, 3, 4, 5, and 6. An oval representing set B also contains the 6, along with 7, 8, and 9. The values 10, 11, and 12 are present but not contained in either set.

Try It

Suppose an experiment has outcomes black, white, red, orange, yellow, green, blue, and purple, where each outcome has an equal chance of occurring. Let event C = {green, blue, purple} and event P = {red, yellow, blue}. Then C AND P = {blue} and C OR P = {green, blue, purple, red, yellow}. Draw a Venn diagram representing this situation.

Example

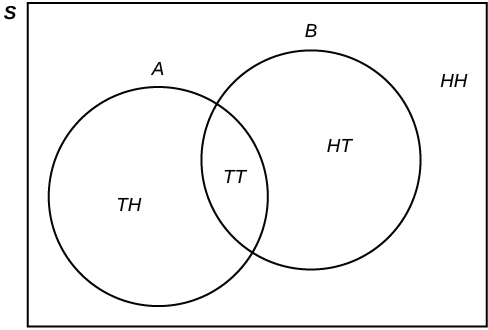
Flip two fair coins. Let [latex]A[/latex] = tails on the first coin. Let [latex]B[/latex] = tails on the second coin. Then [latex]A = \{TT, TH\}[/latex] and [latex]B = \{TT, HT\}[/latex]. Therefore,[latex]A \text{ AND } B = \{TT\}[/latex]. [latex]A \text{ OR } B = \{TH, TT, HT\}[/latex].

The sample space when you flip two fair coins is [latex]X = \{HH, HT, TH, TT\}[/latex]. The outcome [latex]HH[/latex] is in NEITHER [latex]A[/latex] NOR [latex]B[/latex]. The Venn diagram is as follows:

This is a venn diagram. An oval representing set A contains Tails + Heads and Tails + Tails. An oval representing set B also contains Tails + Tails, along with Heads + Tails. The universe S contains Heads + Heads, but this value is not contained in either set A or B.

Try It

Roll a fair, six-sided die. Let A = a prime number of dots is rolled. Let B = an odd number of dots is rolled. Then A = {2, 3, 5} and B = {1, 3, 5}. Therefore, A AND B = {3, 5}. A OR B = {1, 2, 3, 5}. The sample space for rolling a fair die is S = {1, 2, 3, 4, 5, 6}. Draw a Venn diagram representing this situation.

Recall: Convert a Percent to a Decimal

  1. Write the percent as a ratio with the denominator 100.
  2. Convert the fraction to a decimal by dividing the numerator by the denominator.

Example

Forty percent of the students at a local college belong to a club and 50% work part time. Five percent of the students work part time and belong to a club. Draw a Venn diagram showing the relationships. Let C = student belongs to a club and PT = student works part time.This is a venn diagram with one set containing students in clubs and another set containing students working part-time. Both sets share students who are members of clubs and also work part-time. The universe is labeled S.

If a student is selected at random, find

  • the probability that the student belongs to a club. P(C) = 0.40
  • the probability that the student works part time. P(PT) = 0.50
  • the probability that the student belongs to a club AND works part time. P(C AND PT) = 0.05
  • the probability that the student belongs to a club given that the student works part time. [latex]P(C|PT)= \frac{P(C \ \mathrm{AND} \ PT)}{P(PT)} = \frac{0.05}{0.50} = 0.1[/latex]
  • the probability that the student belongs to a club OR works part time. P(C OR PT) = P(C) + P(PT) – P(C AND PT) = 0.40 + 0.50 – 0.05 = 0.85

Try It

Fifty percent of the workers at a factory work a second job, 25% have a spouse who also works, 5% work a second job and have a spouse who also works. Draw a Venn diagram showing the relationships. Let W = works a second job and S = spouse also works.

Recall: The Mean

The mean of a set of n numbers is the arithmetic average of the numbers. It should be greater than the least number and less than the greatest number in the set.

[latex]\mathrm{Mean} = \frac{\mathrm{sum \ of \ values \ in \ the \ set}}{n}[/latex]

Example

A person with type O blood and a negative Rh factor (Rh-) can donate blood to any person with any blood type. Four percent of African Americans have type O blood and a negative RH factor, 5−10% of African Americans have the Rh- factor, and 51% have type O blood.

This is an empty Venn diagram showing two overlapping circles. The left circle is labeled O and the right circle is labeled RH-.

The “O” circle represents the African Americans with type O blood. The “Rh-“ oval represents the African Americans with the Rh- factor.

We will take the average of 5% and 10% and use 7.5% as the percent of African Americans who have the Rh- factor. Let O = African American with Type O blood and R = African American with Rh- factor.

  1. P(O) = ___________
  2. P(R) = ___________
  3. P(O AND R) = ___________
  4. P(O OR R) = ____________
  5. In the Venn Diagram, describe the overlapping area using a complete sentence.
  6. In the Venn Diagram, describe the area in the rectangle but outside both the circle and the oval using a complete sentence.

Try It

In a bookstore, the probability that the customer buys a novel is 0.6, and the probability that the customer buys a non-fiction book is 0.4. Suppose that the probability that the customer buys both is 0.2.

  1. Draw a Venn diagram representing the situation.
  2. Find the probability that the customer buys either a novel or a non-fiction book.
  3. In the Venn diagram, describe the overlapping area using a complete sentence.
  4. Suppose that some customers buy only compact disks. Draw an oval in your Venn diagram representing this event.