Use the definition of a logarithm to solve logarithmic equations

We have already seen that every logarithmic equation ${\mathrm{log}}_{b}\left(x\right)=y$ is equivalent to the exponential equation ${b}^{y}=x$ . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation ${\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3$ . To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x:

{\begin{cases} {l o g}_{2} (2) + {l o g}_{2} (3 x - 5) = 3 \\ {l o g}_{2} (2 (3 x - 5)) = 3 & Apply the product rule of logarithms . \\ {l o g}_{2} (6 x - 10) = 3 & Distribute . \\ 2^{3} = 6 x - 10 & Apply the definition of a logarithm . \\ 8 = 6 x - 10 & Calculate 2^{3} . \\ 18 = 6 x & Add 10 to both sides . \\ x = 3 & Divide by 6 . \end{cases}

$\begin{cases}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Apply the definition of a logarithm}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide by 6}.\hfill \end{cases}$

A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations

For any algebraic expression S and real numbers b and c, where $b>0,\text{ }b\ne 1$ ,

{l o g}_{b} (S) = c if and only if b^{c} = S

${\mathrm{log}}_{b}\left(S\right)=c\text{if and only if}{b}^{c}=S$

Example 9: Using Algebra to Solve a Logarithmic Equation

Solve $2\mathrm{ln}x+3=7$ .

Solution

$\begin{cases}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{ }2\mathrm{ln}x=4\hfill & \text{Subtract 3}.\hfill \\ \text{ }\mathrm{ln}x=2\hfill & \text{Divide by 2}.\hfill \\ \text{ }x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{cases}$

Try It 9

Solve $6+\mathrm{ln}x=10$ .

Solution

Example 10: Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve $2\mathrm{ln}\left(6x\right)=7$ .

Solution

$\begin{cases}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{ }\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide by 2}.\hfill \\ \text{ }6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{ }x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide by 6}.\hfill \end{cases}$

Try It 10

Solve $2\mathrm{ln}\left(x+1\right)=10$ .

Solution

Example 11: Using a Graph to Understand the Solution to a Logarithmic Equation

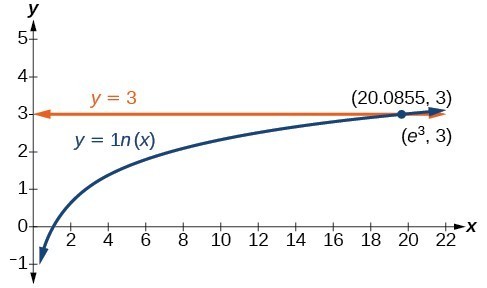
Solve $\mathrm{ln}x=3$ .

Solution

$\begin{cases}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of the natural logarithm}\text{.}\hfill \end{cases}$

Figure 2 represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words ${e}^{3}\approx 20$ . A calculator gives a better approximation: ${e}^{3}\approx 20.0855$ .

Graph of two questions, y=3 and y=ln(x), which intersect at the point (e^3, 3) which is approximately (20.0855, 3).

Figure 2. The graphs of

y = l n x

$y=\mathrm{ln}x$ and y = 3 cross at the point

(e^{3}, 3)

$\left(e^3,3\right)$ , which is approximately (20.0855, 3).

Try It 11

Use a graphing calculator to estimate the approximate solution to the logarithmic equation ${2}^{x}=1000$ to 2 decimal places.

Solution

Exponential and Logarithmic Equations