In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.

Figure 2
We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products.
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and write [latex]\left(0,\text{ }100\right][/latex]. We will discuss interval notation in greater detail later.
Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.
Before we begin, let us review the conventions of interval notation:
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- Parentheses, ( or ), are used to signify that an endpoint is not included, called exclusive.
- Brackets, [ or ], are used to indicate that an endpoint is included, called inclusive.
The table below gives a summary of interval notation.

Example 1: Finding the Domain of a Function as a Set of Ordered Pairs
Find the domain of the following function: [latex]\left\{\left(2,\text{ }10\right),\left(3,\text{ }10\right),\left(4,\text{ }20\right),\left(5,\text{ }30\right),\left(6,\text{ }40\right)\right\}[/latex] .
Solution
First identify the input values. The input value is the first coordinate in an ordered pair. There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.
Try It 1
Find the domain of the function:
[latex]\left\{\left(-5,4\right),\left(0,0\right),\left(5,-4\right),\left(10,-8\right),\left(15,-12\right)\right\}[/latex]
How To: Given a function written in equation form, find the domain.
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Example 2: Finding the Domain of a Function
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].
Solution
The input value, shown by the variable [latex]x[/latex] in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers.
In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,\infty \right)[/latex].
How To: Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example 3: Finding the Domain of a Function Involving a Denominator (Rational Function)
Find the domain of the function [latex]f\left(x\right)=\frac{x+1}{2-x}[/latex].
Solution
When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].
Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].
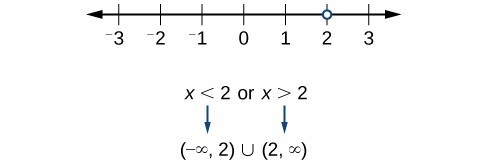
Figure 3
In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].
Try It 3
Find the domain of the function: [latex]f\left(x\right)=\frac{1+4x}{2x - 1}[/latex].
How To: Given a function written in equation form including an even root, find the domain.
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
Example 4: Finding the Domain of a Function with an Even Root
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].
Solution
When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.
Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to [latex]7[/latex], or [latex]\left(-\infty ,7\right][/latex].
Q & A
Can there be functions in which the domain and range do not intersect at all?
Yes. For example, the function [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.