Finding Sums of Infinite Series

When the sum of an infinite geometric series exists, we can calculate the sum. The formula for the sum of an infinite series is related to the formula for the sum of the first $n$ terms of a geometric series.

S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r}

${S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}$

We will examine an infinite series with $r=\frac{1}{2}$ . What happens to ${r}^{n}$ as $n$ increases?

\begin{matrix} {(\frac{1}{2})}^{2} = \frac{1}{4} {(\frac{1}{2})}^{3} = \frac{1}{8} {(\frac{1}{2})}^{4} = \frac{1}{16} \end{matrix}

$\begin{array}{l}{\left(\frac{1}{2}\right)}^{2}=\frac{1}{4}\\ {\left(\frac{1}{2}\right)}^{3}=\frac{1}{8}\\ {\left(\frac{1}{2}\right)}^{4}=\frac{1}{16}\end{array}$

The value of ${r}^{n}$ decreases rapidly. What happens for greater values of $n?$

\begin{matrix} {(\frac{1}{2})}^{10} = \frac{1}{1, 024} {(\frac{1}{2})}^{20} = \frac{1}{1, 048, 576} {(\frac{1}{2})}^{30} = \frac{1}{1, 073, 741, 824} \end{matrix}

$\begin{array}{l}{\left(\frac{1}{2}\right)}^{10}=\frac{1}{1\text{,}024}\hfill \\ {\left(\frac{1}{2}\right)}^{20}=\frac{1}{1\text{,}048\text{,}576}\hfill \\ {\left(\frac{1}{2}\right)}^{30}=\frac{1}{1\text{,}073\text{,}741\text{,}824}\hfill \end{array}$

As $n$ gets very large, ${r}^{n}$ gets very small. We say that, as $n$ increases without bound, ${r}^{n}$ approaches 0. As ${r}^{n}$ approaches 0, $1-{r}^{n}$ approaches 1. When this happens, the numerator approaches ${a}_{1}$ . This give us a formula for the sum of an infinite geometric series.

A General Note: Formula for the Sum of an Infinite Geometric Series

The formula for the sum of an infinite geometric series with [latex]-1 $S=\frac{{a}_{1}}{1-r}$

How To: Given an infinite geometric series, find its sum.

Identify ${a}_{1}$ and $r$ .
Confirm that [latex]-1
Substitute values for ${a}_{1}$ and $r$ into the formula, $S=\frac{{a}_{1}}{1-r}$ .
Simplify to find $S$ .

Example 7: Finding the Sum of an Infinite Geometric Series

Find the sum, if it exists, for the following:

$10+9+8+7+\dots$
$248.6+99.44+39.776+\text{ }\dots$
$\sum _{k=1}^{\infty }4\text{,}374\cdot {\left(-\frac{1}{3}\right)}^{k - 1}$
$\sum _{k=1}^{\infty }\frac{1}{9}\cdot {\left(\frac{4}{3}\right)}^{k}$

Solution

There is not a constant ratio; the series is not geometric.
There is a constant ratio; the series is geometric. ${a}_{1}=248.6$ and $r=\frac{99.44}{248.6}=0.4$ , so the sum exists. Substitute ${a}_{1}=248.6$ and $r=0.4$ into the formula and simplify to find the sum:
$\begin{array}{l}S=\frac{{a}_{1}}{1-r}\hfill \\ S=\frac{248.6}{1 - 0.4}=414.\overline{3}\hfill \end{array}$
The formula is exponential, so the series is geometric with $r=-\frac{1}{3}$ . Find ${a}_{1}$ by substituting $k=1$ into the given explicit formula:
${a}_{1}=4\text{,}374\cdot {\left(-\frac{1}{3}\right)}^{1 - 1}=4\text{,}374$

Substitute ${a}_{1}=4\text{,}374$ and $r=-\frac{1}{3}$ into the formula, and simplify to find the sum:

$\begin{array}{l}S=\frac{{a}_{1}}{1-r}\hfill \\ S=\frac{4\text{,}374}{1-\left(-\frac{1}{3}\right)}=3\text{,}280.5\hfill \end{array}$
The formula is exponential, so the series is geometric, but $r>1$ . The sum does not exist.

Example 8: Finding an Equivalent Fraction for a Repeating Decimal

Find an equivalent fraction for the repeating decimal $0.\overline{3}$

Solution

We notice the repeating decimal $0.\overline{3}=0.333..$ . so we can rewrite the repeating decimal as a sum of terms.

0. ¯ ¯ ¯ 3 = 0.3 + 0.03 + 0.003 + . .

$0.\overline{3}=0.3+0.03+0.003+..$ .

Looking for a pattern, we rewrite the sum, noticing that we see the first term multiplied to 0.1 in the second term, and the second term multiplied to 0.1 in the third term.

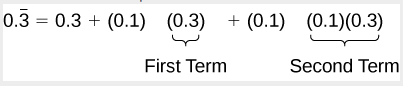
Notice the pattern; we multiply each consecutive term by a common ratio of 0.1 starting with the first term of 0.3. So, substituting into our formula for an infinite geometric sum, we have

S_{n} = \frac{a_{1}}{1 - r} = \frac{0.3}{1 - 0.1} = \frac{0.3}{0.9} = \frac{1}{3}

${S}_{n}=\frac{{a}_{1}}{1-r}=\frac{0.3}{1 - 0.1}=\frac{0.3}{0.9}=\frac{1}{3}$ .

Find the sum, if it exists.

Try It 12

$2+\frac{2}{3}+\frac{2}{9}+..$ .

Solution

Try It 13

$\sum _{k=1}^{\infty }0.76k+1$

Solution

Try It 14

$\sum _{k=1}^{\infty }{\left(-\frac{3}{8}\right)}^{k}$

Solution

Series and Their Notations