An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation $2x+1=7$ has the unique solution $x=3$ because when we substitute 3 for $x$ in the equation, we obtain the true statement $2\left(3\right)+1=7$.

A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area $A$ of a circle in terms of the radius $r$ of the circle: $A=\pi {r}^{2}$. For any value of $r$, the area $A$ can be found by evaluating the expression $\pi {r}^{2}$.

Example 11: Using a Formula

A right circular cylinder with radius $r$ and height $h$ has the surface area $S$ (in square units) given by the formula $S=2\pi r\left(r+h\right)$. Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of $\pi$.

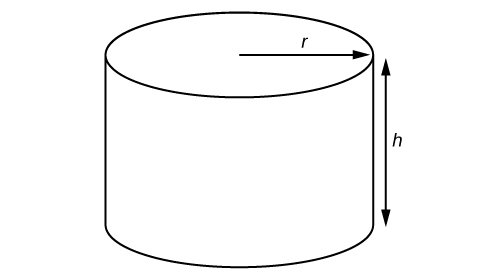
Figure 3. Right circular cylinder

Try It 11

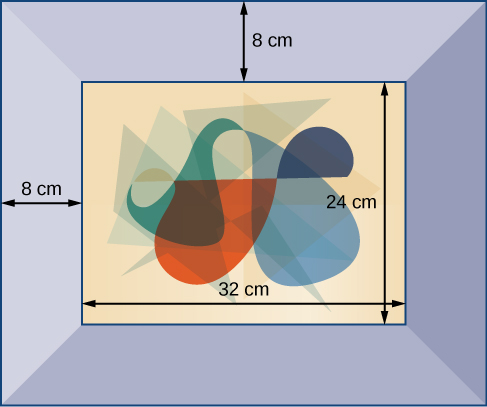
Figure 4

A photograph with length L and width W is placed in a matte of width 8 centimeters (cm). The area of the matte (in square centimeters, or cm²) is found to be $A=\left(L+16\right)\left(W+16\right)-L\cdot W$. Find the area of a matte for a photograph with length 32 cm and width 24 cm.

Solution