Graphing Parabolas with Vertices Not at the Origin

Like other graphs we’ve worked with, the graph of a parabola can be translated. If a parabola is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the vertex will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and [latex]y[/latex] replaced by [latex]\left(y-k\right)[/latex].

To graph parabolas with a vertex [latex]\left(h,k\right)[/latex] other than the origin, we use the standard form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] for parabolas that have an axis of symmetry parallel to the x-axis, and [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex] for parabolas that have an axis of symmetry parallel to the y-axis. These standard forms are given below, along with their general graphs and key features.

A General Note: Standard Forms of Parabolas with Vertex (h, k)

The table and Figure 9 summarize the standard features of parabolas with a vertex at a point [latex]\left(h,k\right)[/latex].

Axis of Symmetry Equation Focus Directrix Endpoints of Latus Rectum
[latex]y=k[/latex] [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] [latex]\left(h+p,\text{ }k\right)[/latex] [latex]x=h-p[/latex] [latex]\left(h+p,\text{ }k\pm 2p\right)[/latex]
[latex]x=h[/latex] [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex] [latex]\left(h,\text{ }k+p\right)[/latex] [latex]y=k-p[/latex] [latex]\left(h\pm 2p,\text{ }k+p\right)[/latex]

Figure 9. (a) When [latex]p>0[/latex], the parabola opens right. (b) When [latex]p<0[/latex], the parabola opens left. (c) When [latex]p>0[/latex], the parabola opens up. (d) When [latex]p<0[/latex], the parabola opens down.

How To: Given a standard form equation for a parabola centered at (h, k), sketch the graph.

  1. Determine which of the standard forms applies to the given equation: [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] or [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex].
  2. Use the standard form identified in Step 1 to determine the vertex, axis of symmetry, focus, equation of the directrix, and endpoints of the latus rectum.
    1. If the equation is in the form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex], then:
      • use the given equation to identify [latex]h[/latex] and [latex]k[/latex] for the vertex, [latex]\left(h,k\right)[/latex]
      • use the value of [latex]k[/latex] to determine the axis of symmetry, [latex]y=k[/latex]
      • set [latex]4p[/latex] equal to the coefficient of [latex]\left(x-h\right)[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p<0[/latex], the parabola opens left.
      • use [latex]h,k[/latex], and [latex]p[/latex] to find the coordinates of the focus, [latex]\left(h+p,\text{ }k\right)[/latex]
      • use [latex]h[/latex] and [latex]p[/latex] to find the equation of the directrix, [latex]x=h-p[/latex]
      • use [latex]h,k[/latex], and [latex]p[/latex] to find the endpoints of the latus rectum, [latex]\left(h+p,k\pm 2p\right)[/latex]
    2. If the equation is in the form [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex], then:
      • use the given equation to identify [latex]h[/latex] and [latex]k[/latex] for the vertex, [latex]\left(h,k\right)[/latex]
      • use the value of [latex]h[/latex] to determine the axis of symmetry, [latex]x=h[/latex]
      • set [latex]4p[/latex] equal to the coefficient of [latex]\left(y-k\right)[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens up. If [latex]p<0[/latex], the parabola opens down.
      • use [latex]h,k[/latex], and [latex]p[/latex] to find the coordinates of the focus, [latex]\left(h,\text{ }k+p\right)[/latex]
      • use [latex]k[/latex] and [latex]p[/latex] to find the equation of the directrix, [latex]y=k-p[/latex]
      • use [latex]h,k[/latex], and [latex]p[/latex] to find the endpoints of the latus rectum, [latex]\left(h\pm 2p,\text{ }k+p\right)[/latex]
  3. Plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

Example 5: Graphing a Parabola with Vertex (h, k) and Axis of Symmetry Parallel to the x-axis

Graph [latex]{\left(y - 1\right)}^{2}=-16\left(x+3\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Solution

The standard form that applies to the given equation is [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex]. Thus, the axis of symmetry is parallel to the x-axis. It follows that:

  • the vertex is [latex]\left(h,k\right)=\left(-3,1\right)[/latex]
  • the axis of symmetry is [latex]y=k=1[/latex]
  • [latex]-16=4p[/latex], so [latex]p=-4[/latex]. Since [latex]p<0[/latex], the parabola opens left.
  • the coordinates of the focus are [latex]\left(h+p,k\right)=\left(-3+\left(-4\right),1\right)=\left(-7,1\right)[/latex]
  • the equation of the directrix is [latex]x=h-p=-3-\left(-4\right)=1[/latex]
  • the endpoints of the latus rectum are [latex]\left(h+p,k\pm 2p\right)=\left(-3+\left(-4\right),1\pm 2\left(-4\right)\right)[/latex], or [latex]\left(-7,-7\right)[/latex] and [latex]\left(-7,9\right)[/latex]

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

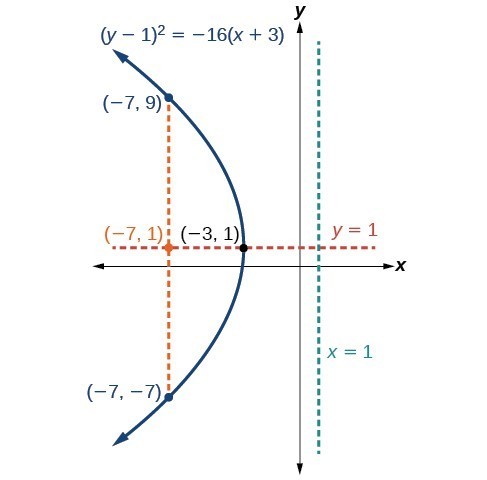
Figure 10

Try It 5

Graph [latex]{\left(y+1\right)}^{2}=4\left(x - 8\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Solution

Example 6: Graphing a Parabola from an Equation Given in General Form

Graph [latex]{x}^{2}-8x - 28y - 208=0[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Solution

Start by writing the equation of the parabola in standard form. The standard form that applies to the given equation is [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex]. Thus, the axis of symmetry is parallel to the y-axis. To express the equation of the parabola in this form, we begin by isolating the terms that contain the variable [latex]x[/latex] in order to complete the square.

[latex]\begin{array}{l}{x}^{2}-8x - 28y - 208=0\hfill \\ \text{ }{x}^{2}-8x=28y+208\hfill \\ \text{ }{x}^{2}-8x+16=28y+208+16\hfill \\ \text{ }{\left(x - 4\right)}^{2}=28y+224\hfill \\ \text{ }{\left(x - 4\right)}^{2}=28\left(y+8\right)\hfill \\ \text{ }{\left(x - 4\right)}^{2}=4\cdot 7\cdot \left(y+8\right)\hfill \end{array}[/latex]

It follows that:

  • the vertex is [latex]\left(h,k\right)=\left(4,-8\right)[/latex]
  • the axis of symmetry is [latex]x=h=4[/latex]
  • since [latex]p=7,p>0[/latex] and so the parabola opens up
  • the coordinates of the focus are [latex]\left(h,k+p\right)=\left(4,-8+7\right)=\left(4,-1\right)[/latex]
  • the equation of the directrix is [latex]y=k-p=-8 - 7=-15[/latex]
  • the endpoints of the latus rectum are [latex]\left(h\pm 2p,k+p\right)=\left(4\pm 2\left(7\right),-8+7\right)[/latex], or [latex]\left(-10,-1\right)[/latex] and [latex]\left(18,-1\right)[/latex]

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

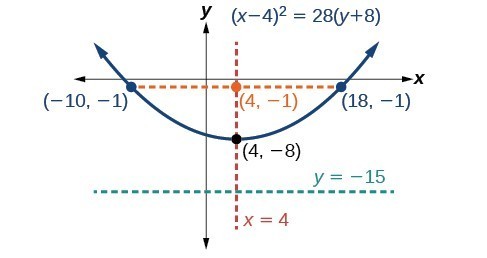
Figure 11

Try It 6

Graph [latex]{\left(x+2\right)}^{2}=-20\left(y - 3\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Solution