1. How do we recognize when an equation is quadratic?

2. When we solve a quadratic equation, how many solutions should we always start out seeking? Explain why when solving a quadratic equation in the form [latex]a{x}^{2}+bx+c=0[/latex] we may graph the equation [latex]y=a{x}^{2}+bx+c[/latex] and have no zeroes (x-intercepts).

3. When we solve a quadratic equation by factoring, why do we move all terms to one side, having zero on the other side?

4. In the quadratic formula, what is the name of the expression under the radical sign [latex]{b}^{2}-4ac[/latex], and how does it determine the number of and nature of our solutions?

5. Describe two scenarios where using the square root property to solve a quadratic equation would be the most efficient method.

For the following exercises, solve the quadratic equation by factoring.

6. [latex]{x}^{2}+4x - 21=0[/latex]

7. [latex]{x}^{2}-9x+18=0[/latex]

8. [latex]2{x}^{2}+9x - 5=0[/latex]

9. [latex]6{x}^{2}+17x+5=0[/latex]

10. [latex]4{x}^{2}-12x+8=0[/latex]

11. [latex]3{x}^{2}-75=0[/latex]

12. [latex]8{x}^{2}+6x - 9=0[/latex]

13. [latex]4{x}^{2}=9[/latex]

14. [latex]2{x}^{2}+14x=36[/latex]

15. [latex]5{x}^{2}=5x+30[/latex]

16. [latex]4{x}^{2}=5x[/latex]

17. [latex]7{x}^{2}+3x=0[/latex]

18. [latex]\frac{x}{3}-\frac{9}{x}=2[/latex]

For the following exercises, solve the quadratic equation by using the square root property.

19. [latex]{x}^{2}=36[/latex]

20. [latex]{x}^{2}=49[/latex]

21. [latex]{\left(x - 1\right)}^{2}=25[/latex]

22. [latex]{\left(x - 3\right)}^{2}=7[/latex]

23. [latex]{\left(2x+1\right)}^{2}=9[/latex]

24. [latex]{\left(x - 5\right)}^{2}=4[/latex]

For the following exercises, solve the quadratic equation by completing the square. Show each step.

25. [latex]{x}^{2}-9x - 22=0[/latex]

26. [latex]2{x}^{2}-8x - 5=0[/latex]

27. [latex]{x}^{2}-6x=13[/latex]

28. [latex]{x}^{2}+\frac{2}{3}x-\frac{1}{3}=0[/latex]

29. [latex]2+z=6{z}^{2}[/latex]

30. [latex]6{p}^{2}+7p - 20=0[/latex]

31. [latex]2{x}^{2}-3x - 1=0[/latex]

For the following exercises, determine the discriminant, and then state how many solutions there are and the nature of the solutions. Do not solve.

32. [latex]2{x}^{2}-6x+7=0[/latex]

33. [latex]{x}^{2}+4x+7=0[/latex]

34. [latex]3{x}^{2}+5x - 8=0[/latex]

35. [latex]9{x}^{2}-30x+25=0[/latex]

36. [latex]2{x}^{2}-3x - 7=0[/latex]

37. [latex]6{x}^{2}-x - 2=0[/latex]

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No Real Solution.

38. [latex]2{x}^{2}+5x+3=0[/latex]

39. [latex]{x}^{2}+x=4[/latex]

40. [latex]2{x}^{2}-8x - 5=0[/latex]

41. [latex]3{x}^{2}-5x+1=0[/latex]

42. [latex]{x}^{2}+4x+2=0[/latex]

43. [latex]4+\frac{1}{x}-\frac{1}{{x}^{2}}=0[/latex]

For the following exercises, enter the expressions into your graphing utility and find the zeroes to the equation (the x-intercepts) by using 2^nd CALC 2:zero. Recall finding zeroes will ask left bound (move your cursor to the left of the zero,enter), then right bound (move your cursor to the right of the zero,enter), then guess (move your cursor between the bounds near the zero, enter). Round your answers to the nearest thousandth.

44. [latex]{\text{Y}}_{1}=4{x}^{2}+3x - 2[/latex]

45. [latex]{\text{Y}}_{1}=-3{x}^{2}+8x - 1[/latex]

46. [latex]{\text{Y}}_{1}=0.5{x}^{2}+x - 7[/latex]

47. To solve the quadratic equation [latex]{x}^{2}+5x - 7=4[/latex], we can graph these two equations

and find the points of intersection. Recall 2^nd CALC 5:intersection. Do this and find the solutions to the nearest tenth.

48. To solve the quadratic equation [latex]0.3{x}^{2}+2x - 4=2[/latex], we can graph these two equations

and find the points of intersection. Recall 2^nd CALC 5:intersection. Do this and find the solutions to the nearest tenth.

49. Beginning with the general form of a quadratic equation, [latex]a{x}^{2}+bx+c=0[/latex], solve for x by using the completing the square method , thus deriving the quadratic formula.

50. Show that the sum of the two solutions to the quadratic equation is [latex]\frac{-b}{a}[/latex].

51. A person has a garden that has a length 10 feet longer than the width. Set up a quadratic equation to find the dimensions of the garden if its area is 119 ft². Solve the quadratic equation to find the length and width.

52. Abercrombie and Fitch stock had a price given as [latex]P=0.2{t}^{2}-5.6t+50.2[/latex], where [latex]t[/latex] is the time in months from 1999 to 2001. ( [latex]t=1[/latex] is January 1999). Find the two months in which the price of the stock was $30.

53. Suppose that an equation is given [latex]p=-2{x}^{2}+280x - 1000[/latex], where [latex]x[/latex] represents the number of items sold at an auction and [latex]p[/latex] is the profit made by the business that ran the auction. How many items sold would make this profit a maximum? Solve this by graphing the expression in your graphing utility and finding the maximum using 2^nd CALC maximum. To obtain a good window for the curve, set [latex]x[/latex] [0,200] and [latex]y[/latex] [0,10000].

54. A formula for the normal systolic blood pressure for a man age [latex]A[/latex], measured in mmHg, is given as [latex]P=0.006{A}^{2}-0.02A+120[/latex]. Find the age to the nearest year of a man whose normal blood pressure measures 125 mmHg.

55. The cost function for a certain company is [latex]C=60x+300[/latex] and the revenue is given by [latex]R=100x - 0.5{x}^{2}[/latex]. Recall that profit is revenue minus cost. Set up a quadratic equation and find two values of x (production level) that will create a profit of $300.

56. A falling object travels a distance given by the formula [latex]d=5t+16{t}^{2}[/latex] ft., where [latex]t[/latex] is measured in seconds. How long will it take for the object to traveled 74 ft.?

57. A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 378 ft². Find the width of the walkway if the garden is 12 ft. wide by 15 ft. long.

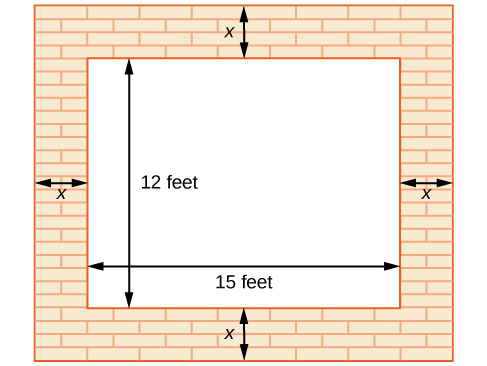
58. An epidemiological study of the spread of a certain influenza strain that hit a small school population found that the total number of students, [latex]P[/latex], who contracted the flu [latex]t[/latex] days after it broke out is given by the model [latex]P=-{t}^{2}+13t+130[/latex], where [latex]1\le t\le 6[/latex]. Find the day that 160 students had the flu. Recall that the restriction on [latex]t[/latex] is at most 6.