1. Explain how to add complex numbers.

2. What is the basic principle in multiplication of complex numbers?

3. Give an example to show the product of two imaginary numbers is not always imaginary.

4. What is a characteristic of the plot of a real number in the complex plane?

For the following exercises, evaluate the algebraic expressions.

5. [latex]\text{If }f\left(x\right)={x}^{2}+x - 4[/latex], evaluate [latex]f\left(2i\right)[/latex].

6. [latex]\text{If }f\left(x\right)={x}^{3}-2[/latex], evaluate [latex]f\left(i\right)[/latex].

7. [latex]\text{If }f\left(x\right)={x}^{2}+3x+5[/latex], evaluate [latex]f\left(2+i\right)[/latex].

8. [latex]\text{If }f\left(x\right)=2{x}^{2}+x - 3[/latex], evaluate [latex]f\left(2 - 3i\right)[/latex].

9. [latex]\text{If }f\left(x\right)=\frac{x+1}{2-x}[/latex], evaluate [latex]f\left(5i\right)[/latex].

10. [latex]\text{If }f\left(x\right)=\frac{1+2x}{x+3}[/latex], evaluate [latex]f\left(4i\right)[/latex].

For the following exercises, determine the number of real and nonreal solutions for each quadratic function shown.

11.

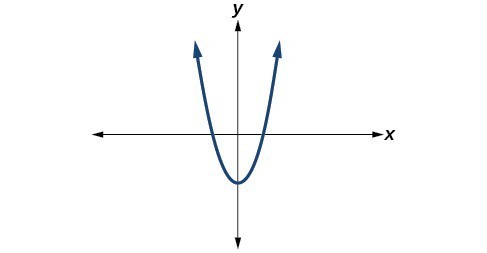
12.

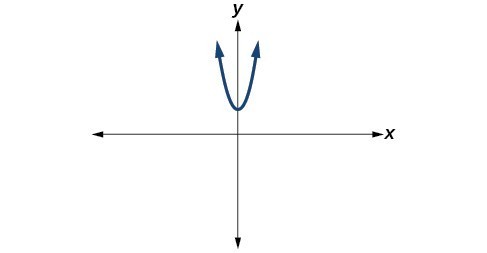
For the following exercises, plot the complex numbers on the complex plane.

13. [latex]1 - 2i[/latex]

14. [latex]-2+3i[/latex]

15. i

16. [latex]-3 - 4i[/latex]

For the following exercises, perform the indicated operation and express the result as a simplified complex number.

17. [latex]\left(3+2i\right)+\left(5 - 3i\right)[/latex]

18. [latex]\left(-2 - 4i\right)+\left(1+6i\right)[/latex]

19. [latex]\left(-5+3i\right)-\left(6-i\right)[/latex]

20. [latex]\left(2 - 3i\right)-\left(3+2i\right)[/latex]

21. [latex]\left(-4+4i\right)-\left(-6+9i\right)[/latex]

22. [latex]\left(2+3i\right)\left(4i\right)[/latex]

23. [latex]\left(5 - 2i\right)\left(3i\right)[/latex]

24. [latex]\left(6 - 2i\right)\left(5\right)[/latex]

25. [latex]\left(-2+4i\right)\left(8\right)[/latex]

26. [latex]\left(2+3i\right)\left(4-i\right)[/latex]

27. [latex]\left(-1+2i\right)\left(-2+3i\right)[/latex]

28. [latex]\left(4 - 2i\right)\left(4+2i\right)[/latex]

29. [latex]\left(3+4i\right)\left(3 - 4i\right)[/latex]

30. [latex]\frac{3+4i}{2}[/latex]

31. [latex]\frac{6 - 2i}{3}[/latex]

32. [latex]\frac{-5+3i}{2i}[/latex]

33. [latex]\frac{6+4i}{i}[/latex]

34. [latex]\frac{2 - 3i}{4+3i}[/latex]

35. [latex]\frac{3+4i}{2-i}[/latex]

36. [latex]\frac{2+3i}{2 - 3i}[/latex]

37. [latex]\sqrt{-9}+3\sqrt{-16}[/latex]

38. [latex]-\sqrt{-4}-4\sqrt{-25}[/latex]

39. [latex]\frac{2+\sqrt{-12}}{2}[/latex]

40. [latex]\frac{4+\sqrt{-20}}{2}[/latex]

41. [latex]{i}^{8}[/latex]

42. [latex]{i}^{15}[/latex]

43. [latex]{i}^{22}[/latex]

For the following exercises, use a calculator to help answer the questions.

44. Evaluate [latex]{\left(1+i\right)}^{k}[/latex] for [latex]k=\text{4, 8, and 12}\text{.}[/latex] Predict the value if [latex]k=16[/latex].

45. Evaluate [latex]{\left(1-i\right)}^{k}[/latex] for [latex]k=\text{2, 6, and 10}\text{.}[/latex] Predict the value if [latex]k=14[/latex].

46. Evaluate [latex]\left(1+i\right)^{k}-\left(1-i\right)^{k}[/latex] for [latex]k=\text{4, 8, and 12}[/latex]. Predict the value for [latex]k=16[/latex].

47. Show that a solution of [latex]{x}^{6}+1=0[/latex] is [latex]\frac{\sqrt{3}}{2}+\frac{1}{2}i[/latex].

48. Show that a solution of [latex]{x}^{8}-1=0[/latex] is [latex]\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i[/latex].

For the following exercises, evaluate the expressions, writing the result as a simplified complex number.

49. [latex]\frac{1}{i}+\frac{4}{{i}^{3}}[/latex]

50. [latex]\frac{1}{{i}^{11}}-\frac{1}{{i}^{21}}[/latex]

51. [latex]{i}^{7}\left(1+{i}^{2}\right)[/latex]

52. [latex]{i}^{-3}+5{i}^{7}[/latex]

53. [latex]\frac{\left(2+i\right)\left(4 - 2i\right)}{\left(1+i\right)}[/latex]

54. [latex]\frac{\left(1+3i\right)\left(2 - 4i\right)}{\left(1+2i\right)}[/latex]

55. [latex]\frac{{\left(3+i\right)}^{2}}{{\left(1+2i\right)}^{2}}[/latex]

56. [latex]\frac{3+2i}{2+i}+\left(4+3i\right)[/latex]

57. [latex]\frac{4+i}{i}+\frac{3 - 4i}{1-i}[/latex]

58. [latex]\frac{3+2i}{1+2i}-\frac{2 - 3i}{3+i}[/latex]