1. If the graphs of two linear functions are parallel, describe the relationship between the slopes and the y-intercepts.
2. If the graphs of two linear functions are perpendicular, describe the relationship between the slopes and the y-intercepts.
3. If a horizontal line has the equation [latex]f\left(x\right)=a[/latex] and a vertical line has the equation [latex]x=a[/latex], what is the point of intersection? Explain why what you found is the point of intersection.
4. Explain how to find a line parallel to a linear function that passes through a given point.
5. Explain how to find a line perpendicular to a linear function that passes through a given point.
For the following exercises, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
6. [latex]\begin{cases}4x - 7y=10\hfill \\ 7x+4y=1\hfill \end{cases}[/latex]
7. [latex]\begin{cases}3y+x=12\\ -y=8x+1\end{cases}[/latex]
8. [latex]\begin{cases}3y+4x=12\\ -6y=8x+1\end{cases}[/latex]
9. [latex]\begin{cases}6x - 9y=10\\ 3x+2y=1\end{cases}[/latex]
10. [latex]\begin{cases}y=\frac{2}{3}x+1\\ 3x+2y=1\end{cases}[/latex]
11. [latex]\begin{cases}y=\frac{3}{4}x+1\\ -3x+4y=1\end{cases}[/latex]
For the following exercises, find the x- and y-intercepts of each equation.
12. [latex]f\left(x\right)=-x+2[/latex]
13. [latex]g\left(x\right)=2x+4[/latex]
14. [latex]h\left(x\right)=3x - 5[/latex]
15. [latex]k\left(x\right)=-5x+1[/latex]
16. [latex]-2x+5y=20[/latex]
17. [latex]7x+2y=56[/latex]
For the following exercises, use the descriptions of each pair of lines given below to find the slopes of Line 1 and Line 2. Is each pair of lines parallel, perpendicular, or neither?
18. Line 1: Passes through [latex]\left(0,6\right)[/latex] and [latex]\left(3,-24\right)[/latex]
Line 2: Passes through [latex]\left(-1,19\right)[/latex] and [latex]\left(8,-71\right)[/latex]
19. Line 1: Passes through [latex]\left(-8,-55\right)[/latex] and [latex]\left(10,89\right)[/latex]
Line 2: Passes through [latex]\left(9,-44\right)[/latex] and [latex]\left(4,-14\right)[/latex]
20. Line 1: Passes through [latex]\left(2,3\right)[/latex] and [latex]\left(4,-1\right)[/latex]
Line 2: Passes through [latex]\left(6,3\right)[/latex] and [latex]\left(8,5\right)[/latex]
21. Line 1: Passes through [latex]\left(1,7\right)[/latex] and [latex]\left(5,5\right)[/latex]
Line 2: Passes through [latex]\left(-1,-3\right)[/latex] and [latex]\left(1,1\right)[/latex]
22. Line 1: Passes through [latex]\left(0,5\right)[/latex] and [latex]\left(3,3\right)[/latex]
Line 2: Passes through [latex]\left(1,-5\right)[/latex] and [latex]\left(3,-2\right)[/latex]
23. Line 1: Passes through [latex]\left(2,5\right)[/latex] and [latex]\left(5,-1\right)[/latex]
Line 2: Passes through [latex]\left(-3,7\right)[/latex] and [latex]\left(3,-5\right)[/latex]
24. Write an equation for a line parallel to [latex]f\left(x\right)=-5x - 3[/latex] and passing through the point [latex]\left(2,\text{ -}12\right)[/latex].
25. Write an equation for a line parallel to [latex]g\left(x\right)=3x - 1[/latex] and passing through the point [latex]\left(4,9\right)[/latex].
26. Write an equation for a line perpendicular to [latex]h\left(t\right)=-2t+4[/latex] and passing through the point [latex]\left(\text{-}4,\text{ -}1\right)[/latex].
27. Write an equation for a line perpendicular to [latex]p\left(t\right)=3t+4[/latex] and passing through the point [latex]\left(3,1\right)[/latex].
28. Find the point at which the line [latex]f\left(x\right)=-2x - 1[/latex] intersects the line [latex]g\left(x\right)=-x[/latex].
29. Find the point at which the line [latex]f\left(x\right)=2x+5[/latex] intersects the line [latex]g\left(x\right)=-3x - 5[/latex].
30. Use algebra to find the point at which the line [latex]f\left(x\right)= -\frac{4}{5}x +\frac{274}{25}[/latex] intersects the line [latex]h\left(x\right)=\frac{9}{4}x+\frac{73}{10}[/latex].
31. Use algebra to find the point at which the line [latex]f\left(x\right)=\frac{7}{4}x+\frac{457}{60}[/latex] intersects the line [latex]g\left(x\right)=\frac{4}{3}x+\frac{31}{5}[/latex].
For the following exercises, the given linear equation with its graph.

32. [latex]f\left(x\right)=-x - 1[/latex]
33. [latex]f\left(x\right)=-2x - 1[/latex]
34. [latex]f\left(x\right)=-\frac{1}{2}x - 1[/latex]
35. [latex]f\left(x\right)=2[/latex]
36. [latex]f\left(x\right)=2+x[/latex]
37. [latex]f\left(x\right)=3x+2[/latex]
For the following exercises, sketch a line with the given features.
38. An x-intercept of [latex]\left(-\text{4},\text{ 0}\right)[/latex] and y-intercept of [latex]\left(0,\text{ -2}\right)[/latex]
39. An x-intercept of [latex]\left(-\text{2},\text{ 0}\right)[/latex] and y-intercept of [latex]\left(0,\text{ 4}\right)[/latex]
40. A y-intercept of [latex]\left(0,\text{ 7}\right)[/latex] and slope [latex]-\frac{3}{2}[/latex]
41. A y-intercept of [latex]\left(0,\text{ 3}\right)[/latex] and slope [latex]\frac{2}{5}[/latex]
42. Passing through the points [latex]\left(-\text{6},\text{ -2}\right)[/latex] and [latex]\left(\text{6},\text{ -6}\right)[/latex]
43. Passing through the points [latex]\left(-\text{3},\text{ -4}\right)[/latex] and [latex]\left(\text{3},\text{ 0}\right)[/latex]
For the following exercises, sketch the graph of each equation.
44. [latex]f\left(x\right)=-2x - 1[/latex]
45. [latex]g\left(x\right)=-3x+2[/latex]
46. [latex]h\left(x\right)=\frac{1}{3}x+2[/latex]
47. [latex]k\left(x\right)=\frac{2}{3}x - 3[/latex]
48. [latex]f\left(t\right)=3+2t[/latex]
49. [latex]p\left(t\right)=-2+3t[/latex]
50. [latex]x=3[/latex]
51. [latex]x=-2[/latex]
52. [latex]r\left(x\right)=4[/latex]
53. [latex]q\left(x\right)=3[/latex]
54. [latex]4x=-9y+36[/latex]
55. [latex]\frac{x}{3}-\frac{y}{4}=1[/latex]
56. [latex]3x - 5y=15[/latex]
57. [latex]3x=15[/latex]
58. [latex]3y=12[/latex]
59. If [latex]g\left(x\right)[/latex] is the transformation of [latex]f\left(x\right)=x[/latex] after a vertical compression by [latex]\frac{3}{4}[/latex], a shift right by 2, and a shift down by 4
a. Write an equation for [latex]g\left(x\right)[/latex].
b. What is the slope of this line?
c. Find the y-intercept of this line.
60. If [latex]g\left(x\right)[/latex] is the transformation of [latex]f\left(x\right)=x[/latex] after a vertical compression by [latex]\frac{1}{3}[/latex], a shift left by 1, and a shift up by 3
a. Write an equation for [latex]g\left(x\right)[/latex].
b. What is the slope of this line?
c. Find the y-intercept of this line.
For the following exercises, write the equation of the line shown in the graph.
61.
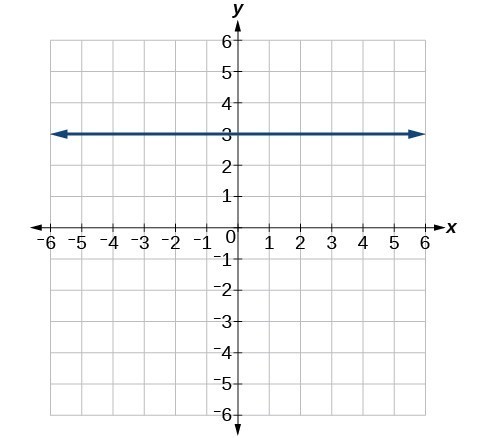
62.
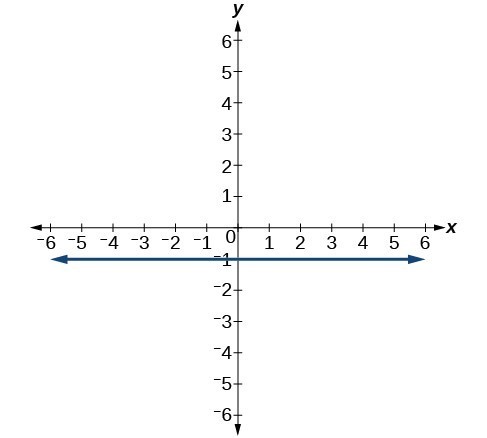
63.
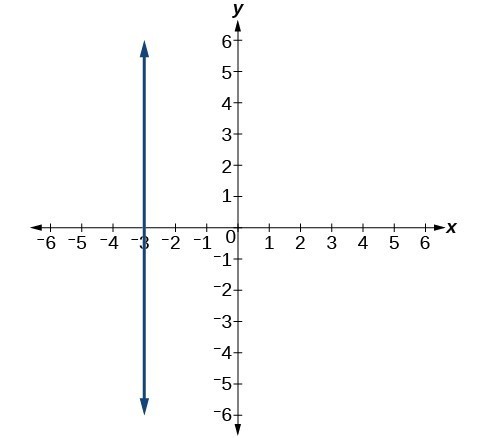
64.
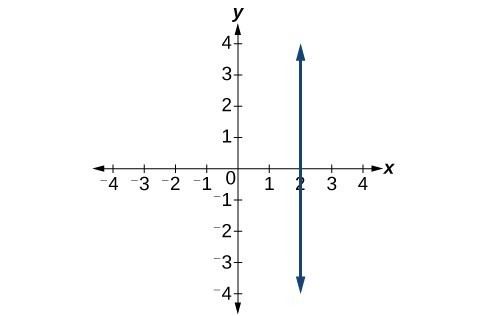
For the following exercises, find the point of intersection of each pair of lines if it exists. If it does not exist, indicate that there is no point of intersection.
65. [latex]\begin{cases}y=\frac{3}{4}x+1\\ -3x+4y=12\end{cases}[/latex]
66. [latex]\begin{cases}2x - 3y=12\\ 5y+x=30\end{cases}[/latex]
67. [latex]\begin{cases}2x=y - 3\\ y+4x=15\end{cases}[/latex]
68. [latex]\begin{cases}x - 2y+2=3\\ x-y=3\end{cases}[/latex]
69. [latex]\begin{cases}5x+3y=-65\\ x-y=-5\end{cases}[/latex]
70. Find the equation of the line parallel to the line [latex]g\left(x\right)=-0.\text{01}x\text{+}\text{2}\text{.01}[/latex] through the point [latex]\left(\text{1},\text{ 2}\right)[/latex].
71. Find the equation of the line perpendicular to the line [latex]g\left(x\right)=-0.\text{01}x\text{+2}\text{.01}[/latex] through the point [latex]\left(\text{1},\text{ 2}\right)[/latex].
For the following exercises, use the functions [latex]f\left(x\right)=-0.\text{1}x\text{+200 and }g\left(x\right)=20x+0.1[/latex].
72. Find the point of intersection of the lines f and g.
73. Where is [latex]f\left(x\right)[/latex] greater than [latex]g\left(x\right)[/latex]? Where is [latex]g\left(x\right)[/latex] greater than [latex]f\left(x\right)[/latex]?
74. A car rental company offers two plans for renting a car.
Plan A: $30 per day and $0.18 per mile
Plan B: $50 per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
75. A cell phone company offers two plans for minutes.
Plan A: $20 per month and $1 for every one hundred texts.
Plan B: $50 per month with free unlimited texts.
How many texts would you need to send per month for plan B to save you money?
76. A cell phone company offers two plans for minutes.
Plan A: $15 per month and $2 for every 300 texts.
Plan B: $25 per month and $0.50 for every 100 texts.
How many texts would you need to send per month for plan B to save you money?