Solutions

Solutions to Try Its

1. The first five terms are {1,6,11,16,21}.

2. The first five terms are {−2,2,−32,1, −58}.

3. The first six terms are {2, 5, 54, 10, 250, 15}.

4. an=(−1)n+19n

5. an=−3n4n

6. an=en−3

7. {2,5,11,23,47}

8. {0,1,1,1,2,3,52, 176}.

9. The first five terms are {1,32,4, 15, 72}.

Solutions to Odd-Numbered Exercises

1. A sequence is an ordered list of numbers that can be either finite or infinite in number. When a finite sequence is defined by a formula, its domain is a subset of the non-negative integers. When an infinite sequence is defined by a formula, its domain is all positive or all non-negative integers.

3. Yes, both sets go on indefinitely, so they are both infinite sequences.

5. A factorial is the product of a positive integer and all the positive integers below it. An exclamation point is used to indicate the operation. Answers may vary. An example of the benefit of using factorial notation is when indicating the product It is much easier to write than it is to write out 13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1.

7. First four terms: −8, −163, −4, −165

9. First four terms: 2, 12, 827, 14 .

11. First four terms: 1.25, −5, 20, −80 .

13. First four terms: 13, 45, 97, 169 .

15. First four terms: −45, 4, −20, 100

17. 13, 45, 97, 169, 2511, 31, 44, 59

19. −0.6,−3,−15,−20,−375,−80,−9375,−320

21. an=n2+3

23. an=2n2n or 2n−1n

25. an=(−12)n−1

27. First five terms: 3, −9, 27, −81, 243

29. First five terms: −1, 1, −9, 2711, 8915

31. 124, 1, 14, 32, 94, 814, 21878, 531,44116

33. 2, 10, 12, 145, 45, 2, 10, 12

35. a1=−8,an=an−1+n

37. a1=35,an=an−1+3

39. 720

41. 665,280

43. First four terms: 1,12,23,32

45. First four terms: −1,2,65,2411

47.
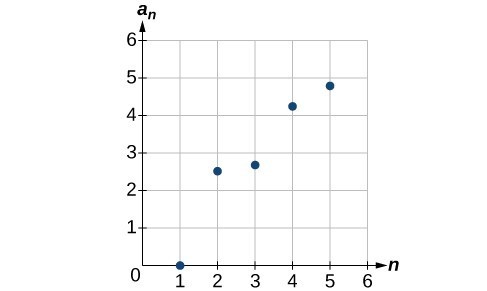
Graph of a scattered plot with points at (1, 0), (2, 5/2), (3, 8/3), (4, 17/4), and (5, 24/5). The x-axis is labeled n and the y-axis is labeled a_n.

49.
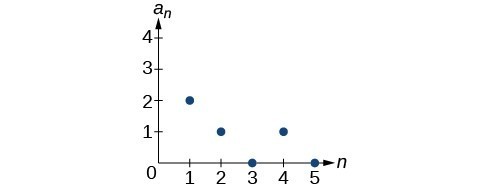
Graph of a scattered plot with points at (1, 2), (2, 1), (3, 0), (4, 1), and (5, 0). The x-axis is labeled n and the y-axis is labeled a_n.

51.
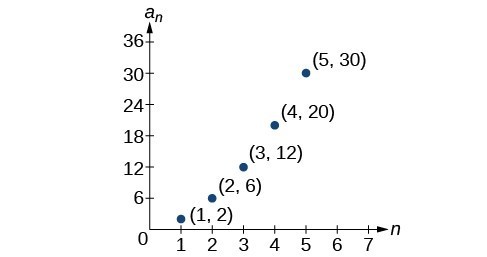
Graph of a scattered plot with labeled points: (1, 2), (2, 6), (3, 12), (4, 20), and (5, 30). The x-axis is labeled n and the y-axis is labeled a_n.

53. an=2n−2

55. a1=6, an=2an−1−5

57. First five terms: 2937,152111,716333,3188999,137242997

59. First five terms: 2,3,5,17,65537

61. a10=7,257,600

63. First six terms: 0.042,0.146,0.875,2.385,4.708

65. First four terms: 5.975,32.765,185.743,1057.25,6023.521

67. If an=−421 is a term in the sequence, then solving the equation −421=−6−8n for n will yield a non-negative integer. However, if −421=−6−8n, then n=51.875 so an=−421 is not a term in the sequence.

69. a1=1,a2=0,an=an−1−an−2

71. (n+2)!(n−1)!=(n+2)⋅(n+1)⋅(n)⋅(n−1)⋅...⋅3⋅2⋅1(n−1)⋅...⋅3⋅2⋅1=n(n+1)(n+2)=n3+3n2+2n