Solutions to Try Its
1. [latex]\left(-\frac{1}{2},\frac{1}{2}\right)[/latex] and [latex]\left(2,8\right)[/latex]
2. [latex]\left(-1,3\right)[/latex]
3. [latex]\left\{\left(1,3\right),\left(1,-3\right),\left(-1,3\right),\left(-1,-3\right)\right\}[/latex]
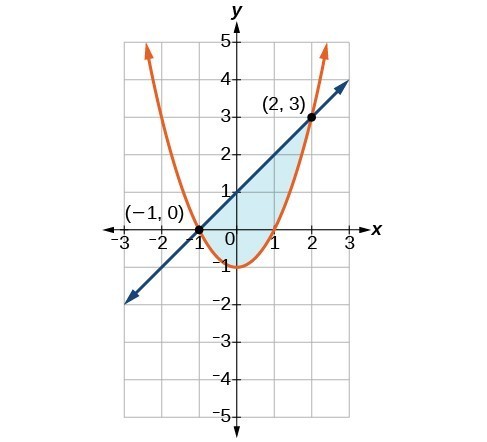
4. Shade the area bounded by the two curves, above the quadratic and below the line.
Solutions to Odd-Numbered Exercises
1. A nonlinear system could be representative of two circles that overlap and intersect in two locations, hence two solutions. A nonlinear system could be representative of a parabola and a circle, where the vertex of the parabola meets the circle and the branches also intersect the circle, hence three solutions.
3. No. There does not need to be a feasible region. Consider a system that is bounded by two parallel lines. One inequality represents the region above the upper line; the other represents the region below the lower line. In this case, no points in the plane are located in both regions; hence there is no feasible region.
5. Choose any number between each solution and plug into [latex]C\left(x\right)[/latex] and [latex]R\left(x\right)[/latex]. If [latex]C\left(x\right)<R\left(x\right),\text{}[/latex] then there is profit.
7. [latex]\left(0,-3\right),\left(3,0\right)[/latex]
9. [latex]\left(-\frac{3\sqrt{2}}{2},\frac{3\sqrt{2}}{2}\right),\left(\frac{3\sqrt{2}}{2},-\frac{3\sqrt{2}}{2}\right)[/latex]
11. [latex]\left(-3,0\right),\left(3,0\right)[/latex]
13. [latex]\left(\frac{1}{4},-\frac{\sqrt{62}}{8}\right),\left(\frac{1}{4},\frac{\sqrt{62}}{8}\right)[/latex]
15. [latex]\left(-\frac{\sqrt{398}}{4},\frac{199}{4}\right),\left(\frac{\sqrt{398}}{4},\frac{199}{4}\right)[/latex]
17. [latex]\left(0,2\right),\left(1,3\right)[/latex]
19. [latex]\left(-\sqrt{\frac{1}{2}\left(\sqrt{5}-1\right)},\frac{1}{2}\left(1-\sqrt{5}\right)\right),\left(\sqrt{\frac{1}{2}\left(\sqrt{5}-1\right)},\frac{1}{2}\left(1-\sqrt{5}\right)\right)[/latex]
21. [latex]\left(5,0\right)[/latex]
23. [latex]\left(0,0\right)[/latex]
25. [latex]\left(3,0\right)[/latex]
27. No Solutions Exist
29. No Solutions Exist
31. [latex]\left(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right),\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right),\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right),\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)[/latex]
33. [latex]\left(2,0\right)[/latex]
35. [latex]\left(-\sqrt{7},-3\right),\left(-\sqrt{7},3\right),\left(\sqrt{7},-3\right),\left(\sqrt{7},3\right)[/latex]
37. [latex]\left(-\sqrt{\frac{1}{2}\left(\sqrt{73}-5\right)},\frac{1}{2}\left(7-\sqrt{73}\right)\right),\left(\sqrt{\frac{1}{2}\left(\sqrt{73}-5\right)},\frac{1}{2}\left(7-\sqrt{73}\right)\right)[/latex]
39.
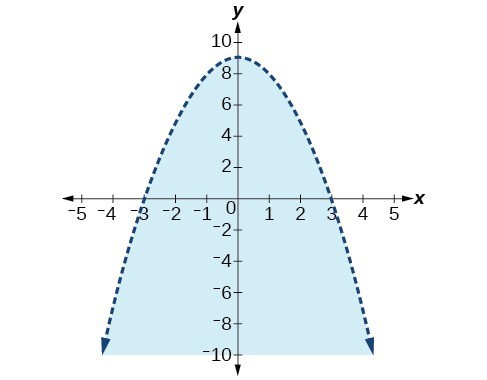
41.
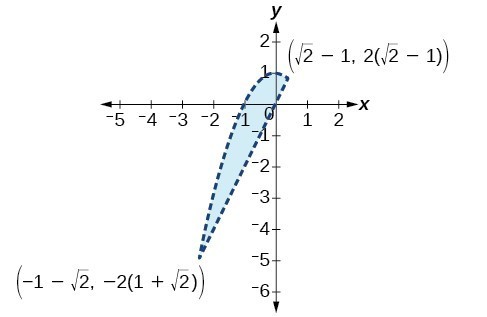
43.
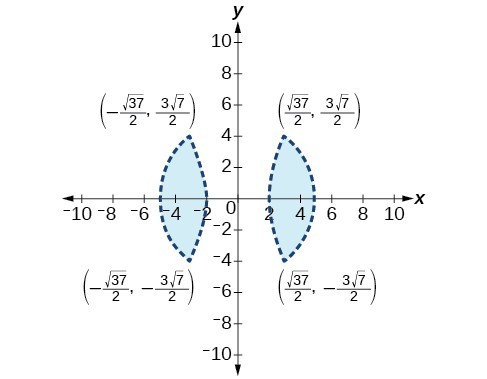
45.
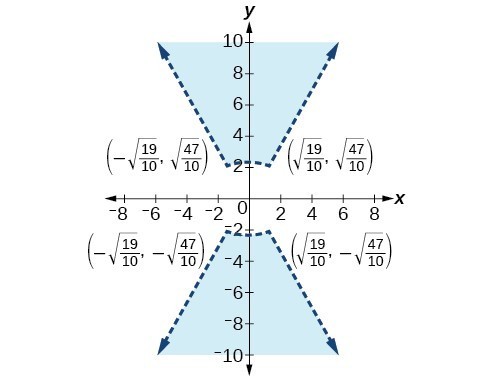
47.
49. [latex]\left(-2\sqrt{\frac{70}{383}},-2\sqrt{\frac{35}{29}}\right),\left(-2\sqrt{\frac{70}{383}},2\sqrt{\frac{35}{29}}\right),\left(2\sqrt{\frac{70}{383}},-2\sqrt{\frac{35}{29}}\right),\left(2\sqrt{\frac{70}{383}},2\sqrt{\frac{35}{29}}\right)[/latex]
51. No Solution Exists
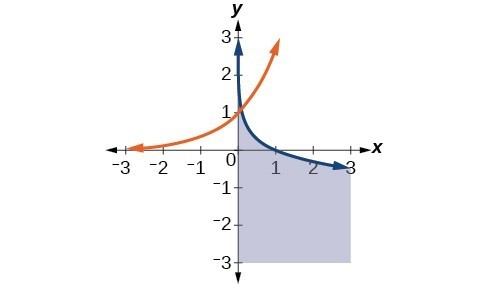
53. [latex]x=0,y>0[/latex] and [latex]0<x<1,\sqrt{x}<y<\frac{1}{x}[/latex]
55. 12, 288
57. 2–20 computers