Solutions to Try Its

1. End behavior: as $x\to \pm \infty , f\left(x\right)\to 0$; Local behavior: as $x\to 0, f\left(x\right)\to \infty$ (there are no x– or y-intercepts)

2. The function and the asymptotes are shifted 3 units right and 4 units down. As $x\to 3,f\left(x\right)\to \infty\\$, and as $x\to \pm \infty ,f\left(x\right)\to -4$.

The function is $f\left(x\right)=\frac{1}{{\left(x - 3\right)}^{2}}-4$.

3. $\frac{12}{11}$

4. The domain is all real numbers except $x=1$ and $x=5$.

5. Removable discontinuity at $x=5$. Vertical asymptotes: $x=0,\text{ }x=1$.

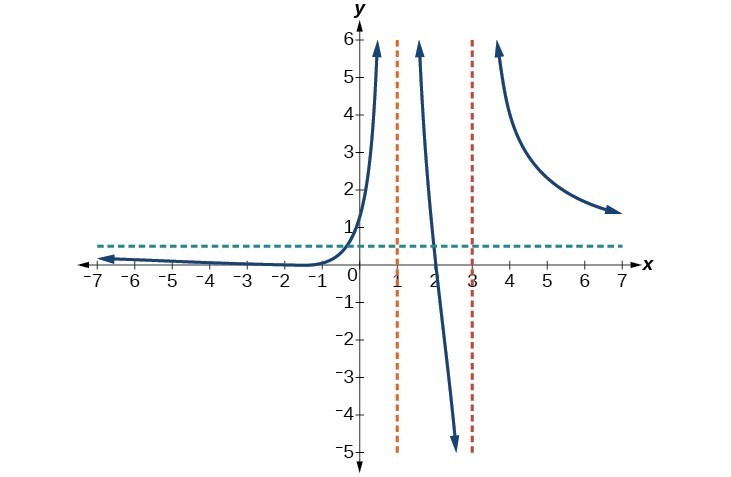
6. Vertical asymptotes at $x=2$ and $x=-3$; horizontal asymptote at $y=4$.

7. For the transformed reciprocal squared function, we find the rational form. $f\left(x\right)=\frac{1}{{\left(x - 3\right)}^{2}}-4=\frac{1 - 4{\left(x - 3\right)}^{2}}{{\left(x - 3\right)}^{2}}=\frac{1 - 4\left({x}^{2}-6x+9\right)}{\left(x - 3\right)\left(x - 3\right)}=\frac{-4{x}^{2}+24x - 35}{{x}^{2}-6x+9}$

Because the numerator is the same degree as the denominator we know that as $x\to \pm \infty , f\left(x\right)\to -4; \text{so } y=-4$ is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is $x=3$, because as $x\to 3,f\left(x\right)\to \infty$. We then set the numerator equal to 0 and find the x-intercepts are at $\left(2.5,0\right)$ and $\left(3.5,0\right)$. Finally, we evaluate the function at 0 and find the y-intercept to be at $\left(0,\frac{-35}{9}\right)$.

8. Horizontal asymptote at $y=\frac{1}{2}$. Vertical asymptotes at $x=1 \text{and} x=3$. y-intercept at $\left(0,\frac{4}{3}.\right)$

x-intercepts at $\left(2,0\right) \text{ and }\left(-2,0\right)$. $\left(-2,0\right)$ is a zero with multiplicity 2, and the graph bounces off the x-axis at this point. $\left(2,0\right)$ is a single zero and the graph crosses the axis at this point.

Solutions to Try Its

1. The rational function will be represented by a quotient of polynomial functions.

3. The numerator and denominator must have a common factor.

5. Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator.

7. $\text{All reals }x\ne -1, 1$

9. $\text{All reals }x\ne -1, -2, 1, 2$

11. V.A. at $x=-\frac{2}{5}$; H.A. at $y=0$; Domain is all reals $x\ne -\frac{2}{5}$

13. V.A. at $x=4, -9$; H.A. at $y=0$; Domain is all reals $x\ne 4, -9$

15. V.A. at $x=0, 4, -4$; H.A. at $y=0$; Domain is all reals $x\ne 0,4, -4$

17. V.A. at $x=-5$; H.A. at $y=0$; Domain is all reals $x\ne 5,-5$

19. V.A. at $x=\frac{1}{3}$; H.A. at $y=-\frac{2}{3}$; Domain is all reals $x\ne \frac{1}{3}$.

21. none

23. $x\text{-intercepts none, }y\text{-intercept }\left(0,\frac{1}{4}\right)$

25. Local behavior: $x\to -{\frac{1}{2}}^{+},f\left(x\right)\to -\infty ,x\to -{\frac{1}{2}}^{-},f\left(x\right)\to \infty$

End behavior: $x\to \pm \infty ,f\left(x\right)\to \frac{1}{2}$

27. Local behavior: $x\to {6}^{+},f\left(x\right)\to -\infty ,x\to {6}^{-},f\left(x\right)\to \infty$, End behavior: $x\to \pm \infty ,f\left(x\right)\to -2$

29. Local behavior: $x\to -{\frac{1}{3}}^{+},f\left(x\right)\to \infty ,x\to -{\frac{1}{3}}^{-}$, $f\left(x\right)\to -\infty ,x\to {\frac{5}{2}}^{-},f\left(x\right)\to \infty ,x\to {\frac{5}{2}}^{+}$ , $f\left(x\right)\to -\infty$

End behavior: $x\to \pm \infty\\$, $f\left(x\right)\to \frac{1}{3}$

31. $y=2x+4$

33. $y=2x$

35. $V.A.\text{ }x=0,H.A.\text{ }y=2$

37. $V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0$

39. $V.A.\text{ }x=-4,\text{ }H.A.\text{ }y=2;\left(\frac{3}{2},0\right);\left(0,-\frac{3}{4}\right)$

41. $V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0,\text{ }\left(0,1\right)$

43. $V.A.\text{ }x=-4,\text{ }x=\frac{4}{3},\text{ }H.A.\text{ }y=1;\left(5,0\right);\left(-\frac{1}{3},0\right);\left(0,\frac{5}{16}\right)$

45. $V.A.\text{ }x=-1,\text{ }H.A.\text{ }y=1;\left(-3,0\right);\left(0,3\right)$

47. $V.A.\text{ }x=4,\text{ }S.A.\text{ }y=2x+9;\left(-1,0\right);\left(\frac{1}{2},0\right);\left(0,\frac{1}{4}\right)$

49. $V.A.\text{ }x=-2,\text{ }x=4,\text{ }H.A.\text{ }y=1,\left(1,0\right);\left(5,0\right);\left(-3,0\right);\left(0,-\frac{15}{16}\right)$

51. $y=50\frac{{x}^{2}-x - 2}{{x}^{2}-25}$

53. $y=7\frac{{x}^{2}+2x - 24}{{x}^{2}+9x+20}$

55. $y=\frac{1}{2}\frac{{x}^{2}-4x+4}{x+1}$

57. $y=4\frac{x - 3}{{x}^{2}-x - 12}$

59. $y=-9\frac{x - 2}{{x}^{2}-9}$

61. $y=\frac{1}{3}\frac{{x}^{2}+x - 6}{x - 1}$

63. $y=-6\frac{{\left(x - 1\right)}^{2}}{\left(x+3\right){\left(x - 2\right)}^{2}}$

65.

x	2.01	2.001	2.0001	1.99	1.999
y	100	1,000	10,000	–100	–1,000

x	10	100	1,000	10,000	100,000
y	.125	.0102	.001	.0001	.00001

Vertical asymptote $x=2$, Horizontal asymptote $y=0$

67.

x	–4.1	–4.01	–4.001	–3.99	–3.999
y	82	802	8,002	–798	–7998

x	10	100	1,000	10,000	100,000
y	1.4286	1.9331	1.992	1.9992	1.999992

Vertical asymptote $x=-4$, Horizontal asymptote $y=2$

69.

x	–.9	–.99	–.999	–1.1	–1.01
y	81	9,801	998,001	121	10,201

x	10	100	1,000	10,000	100,000
y	.82645	.9803	.998	.9998

Vertical asymptote $x=-1$, Horizontal asymptote $y=1$

71. $\left(\frac{3}{2},\infty \right)$

73. $\left(-2,1\right)\cup \left(4,\infty \right)$

75. $\left(2,4\right)$

77. $\left(2,5\right)$

79. $\left(-1,\text{1}\right)$

81. $C\left(t\right)=\frac{8+2t}{300+20t}$

83. After about 6.12 hours.

85. $A\left(x\right)=50{x}^{2}+\frac{800}{x}$. 2 by 2 by 5 feet.

87. $A\left(x\right)=\pi {x}^{2}+\frac{100}{x}$. Radius = 2.52 meters.