Solutions to Try Its

1. y-intercept $\left(0,0\right)$; x-intercepts $\left(0,0\right),\left(-5,0\right),\left(2,0\right)$, and $\left(3,0\right)$

2. The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity.

3.

4. Because f is a polynomial function and since $f\left(1\right)$ is negative and $f\left(2\right)$ is positive, there is at least one real zero between $x=1$ and $x=2$.

5. $f\left(x\right)=-\frac{1}{8}{\left(x - 2\right)}^{3}{\left(x+1\right)}^{2}\left(x - 4\right)$

6. The minimum occurs at approximately the point $\left(0,-6.5\right)$, and the maximum occurs at approximately the point $\left(3.5,7\right)$.

Solutions to Odd-Numbered Exercises

1. The x-intercept is where the graph of the function crosses the x-axis, and the zero of the function is the input value for which $f\left(x\right)=0$.

3. If we evaluate the function at a and at b and the sign of the function value changes, then we know a zero exists between a and b.

5. There will be a factor raised to an even power.

7. $\left(-2,0\right),\left(3,0\right),\left(-5,0\right)$

9. $\left(3,0\right),\left(-1,0\right),\left(0,0\right)$

11. $\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(2,0\right)$

13. $\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(4,0\right)$

15. $\left(2,0\right),\text{ }\left(-2,0\right),\text{ }\left(-1,0\right)$

17. $\left(-2,0\right),\left(2,0\right),\left(\frac{1}{2},0\right)$

19. $\left(1,0\right),\text{ }\left(-1,0\right)$

21. $\left(0,0\right),\left(\sqrt{3},0\right),\left(-\sqrt{3},0\right)$

23. $\left(0,0\right),\text{ }\left(1,0\right)\text{, }\left(-1,0\right),\text{ }\left(2,0\right),\text{ }\left(-2,0\right)$

25. $f\left(2\right)=-10$ and $f\left(4\right)=28$. Sign change confirms.

27. $f\left(1\right)=3$ and $f\left(3\right)=-77$. Sign change confirms.

29. $f\left(0.01\right)=1.000001$ and $f\left(0.1\right)=-7.999$. Sign change confirms.

31. 0 with multiplicity 2, $-\frac{3}{2}$ with multiplicity 5, 4 with multiplicity 2

33. 0 with multiplicity 2, –2 with multiplicity 2

35. $-\frac{2}{3}\text{ with multiplicity }5\text{,}5\text{ with multiplicity }\text{2}$

37. $\text{0}\text{ with multiplicity }4\text{,}2\text{ with multiplicity }1\text{,}-\text{1}\text{ with multiplicity }1$

39. $\frac{3}{2}$ with multiplicity 2, 0 with multiplicity 3

41. $\text{0}\text{ with multiplicity }6\text{,}\frac{2}{3}\text{ with multiplicity }2$

43. x-intercepts, $\left(1, 0\right)$ with multiplicity 2, $\left(-4, 0\right)$ with multiplicity 1, y-intercept $\left(0, 4\right)$. As $x\to -\infty$ , $f\left(x\right)\to -\infty$ , as $x\to \infty$ , $f\left(x\right)\to \infty$ .

45. x-intercepts $\left(3,0\right)$ with multiplicity 3, $\left(2,0\right)$ with multiplicity 2, y-intercept $\left(0,-108\right)$ . As $x\to -\infty$, $f\left(x\right)\to -\infty$ , as $x\to \infty$ , $f\left(x\right)\to \infty$.

47. x-intercepts $\left(0, 0\right),\left(-2, 0\right),\left(4, 0\right)$ with multiplicity 1, y-intercept $\left(0, 0\right)$. As $x\to -\infty$ , $f\left(x\right)\to \infty$ , as $x\to \infty$ , $f\left(x\right)\to -\infty$.

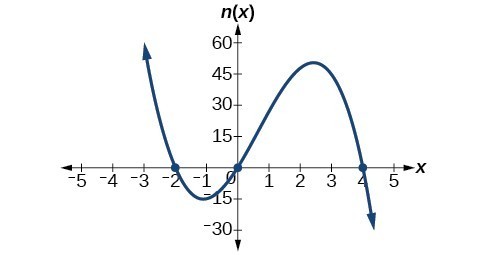
49. $f\left(x\right)=-\frac{2}{9}\left(x - 3\right)\left(x+1\right)\left(x+3\right)$

51. $f\left(x\right)=\frac{1}{4}{\left(x+2\right)}^{2}\left(x - 3\right)$

53. –4, –2, 1, 3 with multiplicity 1

55. –2, 3 each with multiplicity 2

57. $f\left(x\right)=-\frac{2}{3}\left(x+2\right)\left(x - 1\right)\left(x - 3\right)$

59. $f\left(x\right)=\frac{1}{3}{\left(x - 3\right)}^{2}{\left(x - 1\right)}^{2}\left(x+3\right)$

61. $f\left(x\right)=-15{\left(x - 1\right)}^{2}{\left(x - 3\right)}^{3}$

63. $f\left(x\right)=-2\left(x+3\right)\left(x+2\right)\left(x - 1\right)$

65. $f\left(x\right)=-\frac{3}{2}{\left(2x - 1\right)}^{2}\left(x - 6\right)\left(x+2\right)$

67. local max $\left(-\text{.58, -}.62\right)$, local min $\left(\text{.58, -1}\text{.38}\right)$

69. global min $\left(-\text{.63, -}\text{.47}\right)$

71. global min $\text{(}\text{.75, }\text{.89)}$

73. $f\left(x\right)={\left(x - 500\right)}^{2}\left(x+200\right)$

75. $f\left(x\right)=4{x}^{3}-36{x}^{2}+80x$

77. $f\left(x\right)=4{x}^{3}-36{x}^{2}+60x+100$

79. $f\left(x\right)=\pi \left(9{x}^{3}+45{x}^{2}+72x+36\right)$