Solutions to Try Its
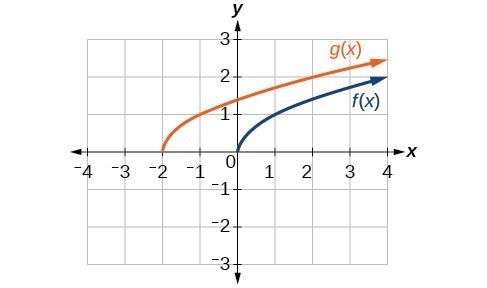
1. The graphs of [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.
2.
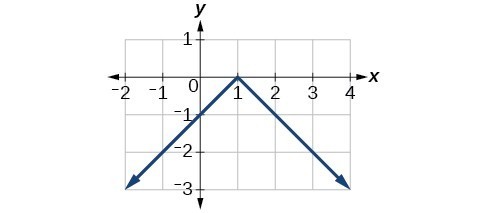
a)
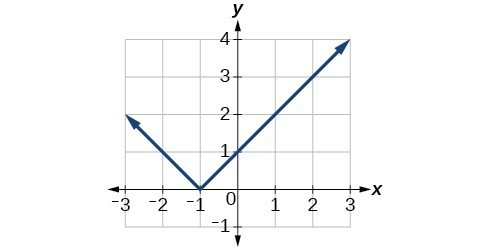
b)
3. [latex]g\left(x\right)=-f\left(x\right)[/latex]
| [latex]x[/latex] | -2 | 0 | 2 | 4 |
| [latex]g\left(x\right)[/latex] | [latex]-5[/latex] | [latex]-10[/latex] | [latex]-15[/latex] | [latex]-20[/latex] |
[latex]h\left(x\right)=f\left(-x\right)[/latex]
| [latex]x[/latex] | -2 | 0 | 2 | 4 |
| [latex]h\left(x\right)[/latex] | 15 | 10 | 5 | unknown |
4. even
5.
| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]g\left(x\right)[/latex] | 9 | 12 | 15 | 0 |
6. [latex]g\left(x\right)=3x - 2[/latex]
7. [latex]g\left(x\right)=f\left(\frac{1}{3}x\right)[/latex] so using the square root function we get [latex]g\left(x\right)=\sqrt{\frac{1}{3}x}[/latex]
8.

9. [latex]g\left(x\right)=\frac{1}{x - 1}+1[/latex]
10. Notice: [latex]g\left(x\right)=f\left(-x\right)[/latex] looks the same as [latex]f\left(x\right)[/latex] .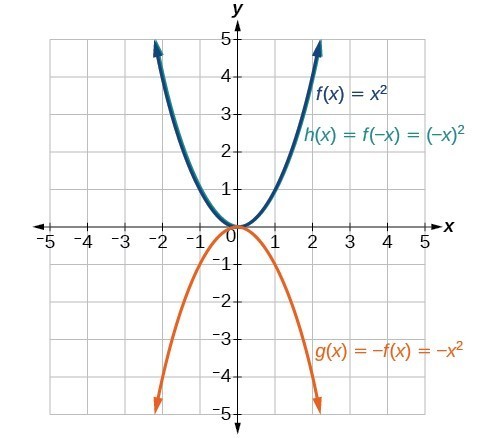
Solution to Odd-Numbered Exercises
1. A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.
3. A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.
5. For a function [latex]f[/latex], substitute [latex]\left(-x\right)[/latex] for [latex]\left(x\right)[/latex] in [latex]f\left(x\right)[/latex]. Simplify. If the resulting function is the same as the original function, [latex]f\left(-x\right)=f\left(x\right)[/latex], then the function is even. If the resulting function is the opposite of the original function, [latex]f\left(-x\right)=-f\left(x\right)[/latex], then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.
7. [latex]g\left(x\right)=|x - 1|-3[/latex]
9. [latex]g\left(x\right)=\frac{1}{{\left(x+4\right)}^{2}}+2[/latex]
11. The graph of [latex]f\left(x+43\right)[/latex] is a horizontal shift to the left 43 units of the graph of [latex]f[/latex].
13. The graph of [latex]f\left(x - 4\right)[/latex] is a horizontal shift to the right 4 units of the graph of [latex]f[/latex].
15. The graph of [latex]f\left(x\right)+8[/latex] is a vertical shift up 8 units of the graph of [latex]f[/latex].
17. The graph of [latex]f\left(x\right)-7[/latex] is a vertical shift down 7 units of the graph of [latex]f[/latex].
19. The graph of [latex]f\left(x+4\right)-1[/latex] is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of [latex]f[/latex].
21. decreasing on [latex]\left(-\infty ,-3\right)[/latex] and increasing on [latex]\left(-3,\infty \right)[/latex]
23. decreasing on [latex]\left(0,\infty \right)[/latex]
25.

27.
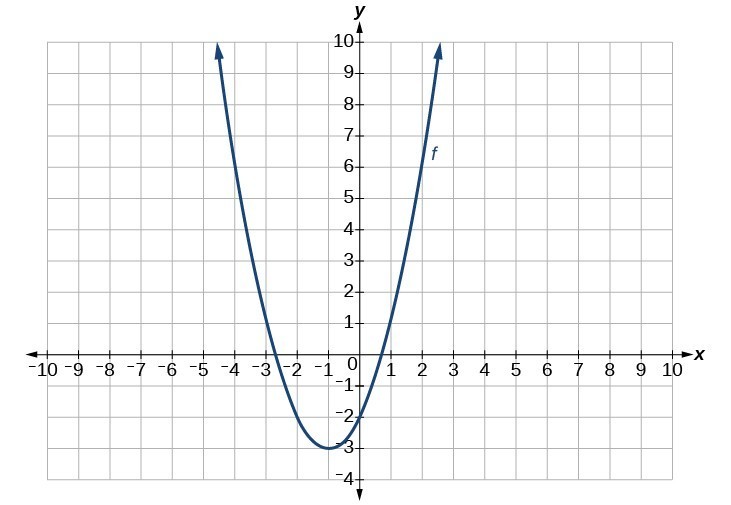
29.

31. [latex]g\left(x\right)=f\left(x - 1\right),h\left(x\right)=f\left(x\right)+1[/latex]
33. [latex]f\left(x\right)=|x - 3|-2[/latex]
35. [latex]f\left(x\right)=\sqrt{x+3}-1[/latex]
37. [latex]f\left(x\right)={\left(x - 2\right)}^{2}[/latex]
39. [latex]f\left(x\right)=|x+3|-2[/latex]
41. [latex]f\left(x\right)=-\sqrt{x}[/latex]
43. [latex]f\left(x\right)=-{\left(x+1\right)}^{2}+2[/latex]
45. [latex]f\left(x\right)=\sqrt{-x}+1[/latex]
47. even
49. odd
51. even
53. The graph of [latex]g[/latex] is a vertical reflection (across the [latex]x[/latex] -axis) of the graph of [latex]f[/latex].
55. The graph of [latex]g[/latex] is a vertical stretch by a factor of 4 of the graph of [latex]f[/latex].
57. The graph of [latex]g[/latex] is a horizontal compression by a factor of [latex]\frac{1}{5}[/latex] of the graph of [latex]f[/latex].
59. The graph of [latex]g[/latex] is a horizontal stretch by a factor of 3 of the graph of [latex]f[/latex].
61. The graph of [latex]g[/latex] is a horizontal reflection across the [latex]y[/latex] -axis and a vertical stretch by a factor of 3 of the graph of [latex]f[/latex].
63. [latex]g\left(x\right)=|-4x|[/latex]
65. [latex]g\left(x\right)=\frac{1}{3{\left(x+2\right)}^{2}}-3[/latex]
67. [latex]g\left(x\right)=\frac{1}{2}{\left(x - 5\right)}^{2}+1[/latex]
69. The graph of the function [latex]f\left(x\right)={x}^{2}[/latex] is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.

71. The graph of [latex]f\left(x\right)=|x|[/latex] is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.

73. The graph of the function [latex]f\left(x\right)={x}^{3}[/latex] is compressed vertically by a factor of [latex]\frac{1}{2}[/latex].

75. The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.

77. The graph of [latex]f\left(x\right)=\sqrt{x}[/latex] is shifted right 4 units and then reflected across the vertical line [latex]x=4[/latex].

79.
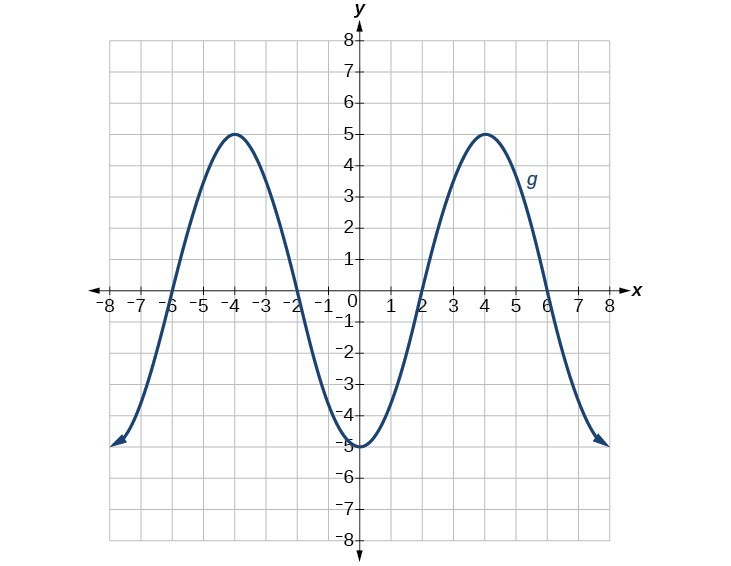
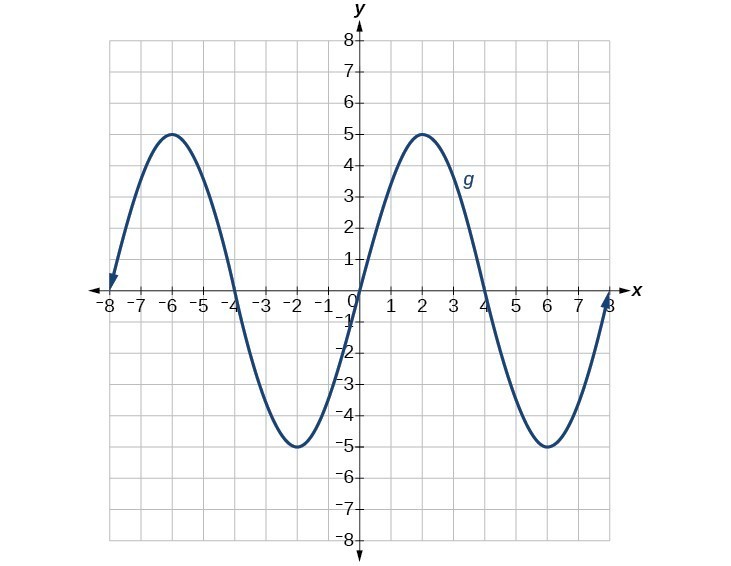
81.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.