Solve an absolute value equation

Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as [latex]{8}=\left|{2}x - {6}\right|[/latex], we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.

[latex]\begin{cases}2x - 6=8\hfill & \text{or}\hfill & 2x - 6=-8\hfill \\ 2x=14\hfill & \hfill & 2x=-2\hfill \\ x=7\hfill & \hfill & x=-1\hfill \end{cases}[/latex]

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

An absolute value equation is an equation in which the unknown variable appears in absolute value bars. For example,

[latex]\begin{cases}|x|=4,\hfill \\ |2x - 1|=3\hfill \\ |5x+2|-4=9\hfill \end{cases}[/latex]

A General Note: Solutions to Absolute Value Equations

For real numbers [latex]A[/latex] and [latex]B[/latex], an equation of the form [latex]|A|=B[/latex], with [latex]B\ge 0[/latex], will have solutions when [latex]A=B[/latex] or [latex]A=-B[/latex]. If [latex]B<0[/latex], the equation [latex]|A|=B[/latex] has no solution.

How To: Given the formula for an absolute value function, find the horizontal intercepts of its graph.

  1. Isolate the absolute value term.
  2. Use [latex]|A|=B[/latex] to write [latex]A=B[/latex] or [latex]\mathrm{-A}=B[/latex], assuming [latex]B>0[/latex].
  3. Solve for [latex]x[/latex].

Example 4: Finding the Zeros of an Absolute Value Function

For the function [latex]f\left(x\right)=|4x+1|-7[/latex] , find the values of [latex]x[/latex] such that [latex]\text{ }f\left(x\right)=0[/latex] .

Solution

[latex]\begin{cases}0=|4x+1|-7\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Substitute 0 for }f\left(x\right).\hfill \\ 7=|4x+1|\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Isolate the absolute value on one side of the equation}.\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ 7=4x+1\hfill & \text{or}\hfill & \hfill & \hfill & \hfill & -7=4x+1\hfill & \text{Break into two separate equations and solve}.\hfill \\ 6=4x\hfill & \hfill & \hfill & \hfill & \hfill & -8=4x\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ x=\frac{6}{4}=1.5\hfill & \hfill & \hfill & \hfill & \hfill & \text{ }x=\frac{-8}{4}=-2\hfill & \hfill \end{cases}[/latex]

Graph an absolute function with x-intercepts at -2 and 1.5.

Figure 9

The function outputs 0 when [latex]x=1.5[/latex] or [latex]x=-2[/latex].

Try It 4

For the function [latex]f\left(x\right)=|2x - 1|-3[/latex], find the values of [latex]x[/latex] such that [latex]f\left(x\right)=0[/latex].

Solution

Q & A

Should we always expect two answers when solving [latex]|A|=B?[/latex]

No. We may find one, two, or even no answers. For example, there is no solution to [latex]2+|3x - 5|=1[/latex].

How To: Given an absolute value equation, solve it.

  1. Isolate the absolute value term.
  2. Use [latex]|A|=B[/latex] to write [latex]A=B[/latex] or [latex]A=\mathrm{-B}[/latex].
  3. Solve for [latex]x[/latex].

Example 5: Solving an Absolute Value Equation

Solve [latex]1=4|x - 2|+2[/latex].

Solution

Isolating the absolute value on one side of the equation gives the following.

[latex]\begin{cases}1=4|x - 2|+2\hfill \\ -1=4|x - 2|\hfill \\ -\frac{1}{4}=|x - 2|\hfill \end{cases}[/latex]

The absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value. At this point, we notice that this equation has no solutions.

Q & A

In Example 5, if [latex]f\left(x\right)=1[/latex] and [latex]g\left(x\right)=4|x - 2|+2[/latex] were graphed on the same set of axes, would the graphs intersect?

No. The graphs of [latex]f[/latex] and [latex]g[/latex] would not intersect. This confirms, graphically, that the equation [latex]1=4|x - 2|+2[/latex] has no solution.

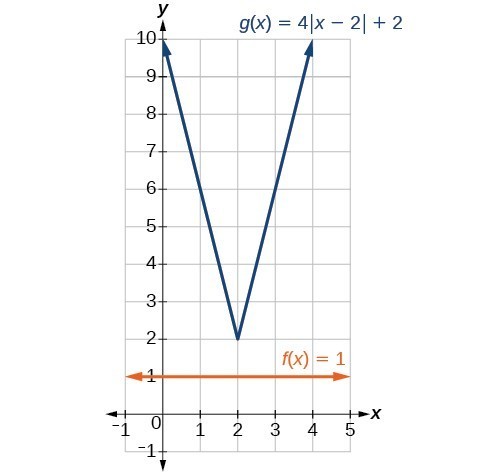
Graph of g(x)=4|x-2|+2 and f(x)=1.

Figure 10

Try It 5

Find where the graph of the function [latex]f\left(x\right)=-|x+2|+3[/latex] intersects the horizontal and vertical axes.

Solution