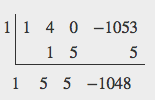Solve real-world applications of polynomial equations

We have now introduced a variety of tools for solving polynomial equations. Let’s use these tools to solve the bakery problem from the beginning of the section.

Example 8: Solving Polynomial Equations

A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be four inches longer than the width of the cake and the height of the cake to be one-third of the width. What should the dimensions of the cake pan be?

Solution

Begin by writing an equation for the volume of the cake. The volume of a rectangular solid is given by [latex]V=lwh[/latex]. We were given that the length must be four inches longer than the width, so we can express the length of the cake as [latex]l=w+4[/latex]. We were given that the height of the cake is one-third of the width, so we can express the height of the cake as [latex]h=\frac{1}{3}w[/latex]. Let’s write the volume of the cake in terms of width of the cake.

[latex]\begin{cases}V=\left(w+4\right)\left(w\right)\left(\frac{1}{3}w\right)\\ V=\frac{1}{3}{w}^{3}+\frac{4}{3}{w}^{2}\end{cases}[/latex]

Substitute the given volume into this equation.

[latex]\begin{cases}\text{ }351=\frac{1}{3}{w}^{3}+\frac{4}{3}{w}^{2}\hfill & \text{Substitute 351 for }V.\hfill \\ 1053={w}^{3}+4{w}^{2}\hfill & \text{Multiply both sides by 3}.\hfill \\ \text{ }0={w}^{3}+4{w}^{2}-1053 \hfill & \text{Subtract 1053 from both sides}.\hfill \end{cases}[/latex]

Descartes’ rule of signs tells us there is one positive solution. The Rational Zero Theorem tells us that the possible rational zeros are [latex]\pm 3,\pm 9,\pm 13,\pm 27,\pm 39,\pm 81,\pm 117,\pm 351[/latex], and [latex]\pm 1053[/latex]. We can use synthetic division to test these possible zeros. Only positive numbers make sense as dimensions for a cake, so we need not test any negative values. Let’s begin by testing values that make the most sense as dimensions for a small sheet cake. Use synthetic division to check [latex]x=1[/latex].

Synthetic Division with divisor = 1, and quotient = {1, 4, 0, -1053}. Solution is {1, 5, 5, -1048}

Since 1 is not a solution, we will check [latex]x=3[/latex].


.

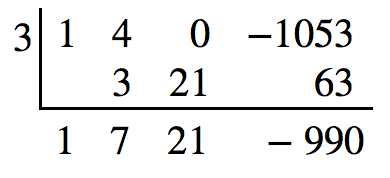
Since 3 is not a solution either, we will test [latex]x=9[/latex].


.

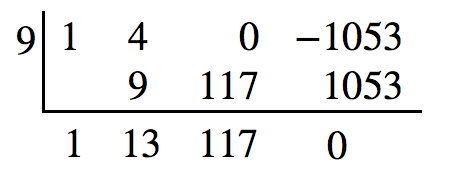
Synthetic division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.

[latex]l=w+4=9+4=13\text{ and }h=\frac{1}{3}w=\frac{1}{3}\left(9\right)=3[/latex]

The sheet cake pan should have dimensions 13 inches by 9 inches by 3 inches.

Try It 7

A shipping container in the shape of a rectangular solid must have a volume of 84 cubic meters. The client tells the manufacturer that, because of the contents, the length of the container must be one meter longer than the width, and the height must be one meter greater than twice the width. What should the dimensions of the container be?