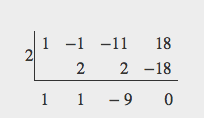Polynomial division can be used to solve a variety of application problems involving expressions for area and volume. We looked at an application at the beginning of this section. Now we will solve that problem in the following example.
Example 6: Using Polynomial Division in an Application Problem
The volume of a rectangular solid is given by the polynomial [latex]3{x}^{4}-3{x}^{3}-33{x}^{2}+54x.\\[/latex] The length of the solid is given by 3x and the width is given by x – 2. Find the height of the solid.
Solution
There are a few ways to approach this problem. We need to divide the expression for the volume of the solid by the expressions for the length and width. Let us create a sketch.

Figure 3
We can now write an equation by substituting the known values into the formula for the volume of a rectangular solid.
To solve for h, first divide both sides by 3x.
Now solve for h using synthetic division.
The quotient is [latex]{x}^{2}+x - 9\\[/latex] and the remainder is 0. The height of the solid is [latex]{x}^{2}+x - 9.\\[/latex]
Try It 3
The area of a rectangle is given by [latex]3{x}^{3}+14{x}^{2}-23x+6.\\[/latex] The width of the rectangle is given by x + 6. Find an expression for the length of the rectangle.