Using the Binomial Theorem | College Algebra

When we expand ${\left(x+y\right)}^{n}$ by multiplying, the result is called a binomial expansion, and it includes binomial coefficients. If we wanted to expand ${\left(x+y\right)}^{52}$ , we might multiply $\left(x+y\right)$ by itself fifty-two times. This could take hours! If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions.

\begin{matrix} {(x + y)}^{2} = x^{2} + 2 x y + y^{2} {(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} {(x + y)}^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4} \end{matrix}

$\begin{array}{l}{\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}$

First, let’s examine the exponents. With each successive term, the exponent for $x$ decreases and the exponent for $y$ increases. The sum of the two exponents is $n$ for each term.

Next, let’s examine the coefficients. Notice that the coefficients increase and then decrease in a symmetrical pattern. The coefficients follow a pattern:

(\begin{matrix} n 0 \end{matrix}), (\begin{matrix} n 1 \end{matrix}), (\begin{matrix} n 2 \end{matrix}), . . ., (\begin{matrix} n n \end{matrix})

$\left(\begin{array}{c}n\\ 0\end{array}\right),\left(\begin{array}{c}n\\ 1\end{array}\right),\left(\begin{array}{c}n\\ 2\end{array}\right),...,\left(\begin{array}{c}n\\ n\end{array}\right)$ .

These patterns lead us to the Binomial Theorem, which can be used to expand any binomial.

\begin{matrix} {(x + y)}^{n} & = \sum_{k = 0}^{n} (\begin{matrix} n k \end{matrix}) x^{n - k} y^{k} = x^{n} + (\begin{matrix} n 1 \end{matrix}) x^{n - 1} y + (\begin{matrix} n 2 \end{matrix}) x^{n - 2} y^{2} + . . . + (\begin{matrix} n n - 1 \end{matrix}) x y^{n - 1} + y^{n} \end{matrix}

$\begin{array}{ll}{\left(x+y\right)}^{n}\hfill & =\sum _{k=0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}\hfill \\ \hfill & ={x}^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right){x}^{n - 1}y+\left(\begin{array}{c}n\\ 2\end{array}\right){x}^{n - 2}{y}^{2}+...+\left(\begin{array}{c}n\\ n - 1\end{array}\right)x{y}^{n - 1}+{y}^{n}\hfill \end{array}$

Another way to see the coefficients is to examine the expansion of a binomial in general form, $x+y$ , to successive powers 1, 2, 3, and 4.

\begin{matrix} {(x + y)}^{1} = x + y {(x + y)}^{2} = x^{2} + 2 x y + y^{2} {(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} {(x + y)}^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4} \end{matrix}

$\begin{array}{l}{\left(x+y\right)}^{1}=x+y\hfill \\ {\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}$

Can you guess the next expansion for the binomial ${\left(x+y\right)}^{5}?$

Figure 1

See Figure 1, which illustrates the following:

There are $n+1$ terms in the expansion of ${\left(x+y\right)}^{n}$ .
The degree (or sum of the exponents) for each term is $n$ .
The powers on $x$ begin with $n$ and decrease to 0.
The powers on $y$ begin with 0 and increase to $n$ .
The coefficients are symmetric.

To determine the expansion on ${\left(x+y\right)}^{5}$ , we see $n=5$ , thus, there will be 5+1 = 6 terms. Each term has a combined degree of 5. In descending order for powers of $x$ , the pattern is as follows:

Introduce ${x}^{5}$ , and then for each successive term reduce the exponent on $x$ by 1 until ${x}^{0}=1$ is reached.
Introduce ${y}^{0}=1$ , and then increase the exponent on $y$ by 1 until ${y}^{5}$ is reached.
${x}^{5},{x}^{4}y,{x}^{3}{y}^{2},{x}^{2}{y}^{3},x{y}^{4},{y}^{5}$

The next expansion would be

{(x + y)}^{5} = x^{5} + 5 x^{4} y + 10 x^{3} y^{2} + 10 x^{2} y^{3} + 5 x y^{4} + y^{5}

${\left(x+y\right)}^{5}={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}$ .

But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal’s Triangle, shown in Figure 2.

Figure 2

To generate Pascal’s Triangle, we start by writing a 1. In the row below, row 2, we write two 1’s. In the 3^rd row, flank the ends of the rows with 1’s, and add $1+1$ to find the middle number, 2. In the $n\text{th}$ row, flank the ends of the row with 1’s. Each element in the triangle is the sum of the two elements immediately above it.

To see the connection between Pascal’s Triangle and binomial coefficients, let us revisit the expansion of the binomials in general form.

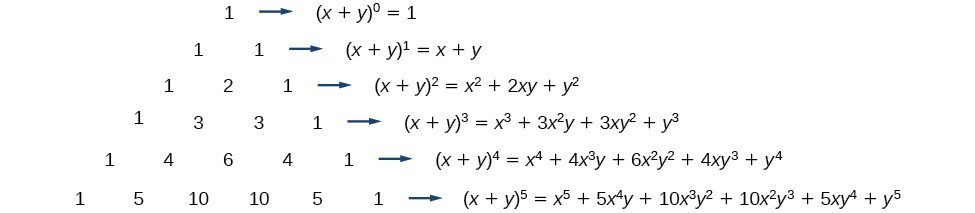
Pascal's Triangle expanded to show the values of the triangle as x and y terms with exponents

A General Note: The Binomial Theorem

The Binomial Theorem is a formula that can be used to expand any binomial.

\begin{matrix} {(x + y)}^{n} & = \sum_{k = 0}^{n} (\begin{matrix} n k \end{matrix}) x^{n - k} y^{k} = x^{n} + (\begin{matrix} n 1 \end{matrix}) x^{n - 1} y + (\begin{matrix} n 2 \end{matrix}) x^{n - 2} y^{2} + . . . + (\begin{matrix} n n - 1 \end{matrix}) x y^{n - 1} + y^{n} \end{matrix}

How To: Given a binomial, write it in expanded form.

Determine the value of $n$ according to the exponent.
Evaluate the $k=0$ through $k=n$ using the Binomial Theorem formula.
Simplify.

Example 2: Expanding a Binomial

Write in expanded form.

${\left(x+y\right)}^{5}$
${\left(3x-y\right)}^{4}$

Solution

Substitute $n=5$ into the formula. Evaluate the $k=0$ through $k=5$ terms. Simplify.
$\begin{array}{ll}{\left(x+y\right)}^{5}\hfill & =\left(\begin{array}{c}5\\ 0\end{array}\right){x}^{5}{y}^{0}+\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}{y}^{1}+\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}+\left(\begin{array}{c}5\\ 3\end{array}\right){x}^{2}{y}^{3}+\left(\begin{array}{c}5\\ 4\end{array}\right){x}^{1}{y}^{4}+\left(\begin{array}{c}5\\ 5\end{array}\right){x}^{0}{y}^{5}\hfill \\ {\left(x+y\right)}^{5}\hfill & ={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}\hfill \end{array}$
Substitute $n=4$ into the formula. Evaluate the $k=0$ through $k=4$ terms. Notice that $3x$ is in the place that was occupied by $x$ and that $-y$ is in the place that was occupied by $y$ . So we substitute them. Simplify.
$\begin{array}{ll}{\left(3x-y\right)}^{4}\hfill & =\left(\begin{array}{c}4\\ 0\end{array}\right){\left(3x\right)}^{4}{\left(-y\right)}^{0}+\left(\begin{array}{c}4\\ 1\end{array}\right){\left(3x\right)}^{3}{\left(-y\right)}^{1}+\left(\begin{array}{c}4\\ 2\end{array}\right){\left(3x\right)}^{2}{\left(-y\right)}^{2}+\left(\begin{array}{c}4\\ 3\end{array}\right){\left(3x\right)}^{1}{\left(-y\right)}^{3}+\left(\begin{array}{c}4\\ 4\end{array}\right){\left(3x\right)}^{0}{\left(-y\right)}^{4}\hfill \\ {\left(3x-y\right)}^{4}\hfill & =81{x}^{4}-108{x}^{3}y+54{x}^{2}{y}^{2}-12x{y}^{3}+{y}^{4}\hfill \end{array}$

Analysis of the Solution

Notice the alternating signs in part b. This happens because $\left(-y\right)$ raised to odd powers is negative, but $\left(-y\right)$ raised to even powers is positive. This will occur whenever the binomial contains a subtraction sign.

Try It 2

Write in expanded form.

a. ${\left(x-y\right)}^{5}$

b. ${\left(2x+5y\right)}^{3}$

Solution