When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula. Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint formula states how to find the coordinates of the midpoint [latex]M[/latex].
A graphical view of a midpoint is shown in Figure 14. Notice that the line segments on either side of the midpoint are congruent.
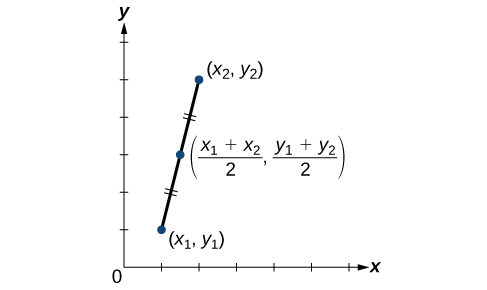
Figure 14
Example 7: Finding the Midpoint of the Line Segment
Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].
Solution
Use the formula to find the midpoint of the line segment.
Try It 2
Find the midpoint of the line segment with endpoints [latex]\left(-2,-1\right)[/latex] and [latex]\left(-8,6\right)[/latex].
Example 8: Finding the Center of a Circle
The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.
Solution
The center of a circle is the center, or midpoint, of its diameter. Thus, the midpoint formula will yield the center point.