Reflection and Transmission

When the medium changes, a wave often experiences partial transmission and partial refection at the interface.

When the medium through which a wave travels suddenly changes, the wave often experiences partial transmission and partial refection at the interface. Reflection is a wave phenomenon that changes the direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Transmission permits the passage of wave, with some or none of the incident wave being absorbed. Reflection and transmission often occur at the same time.

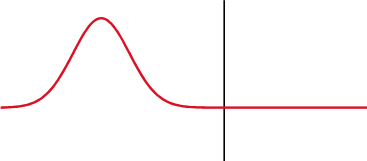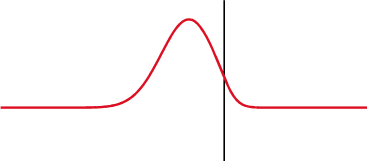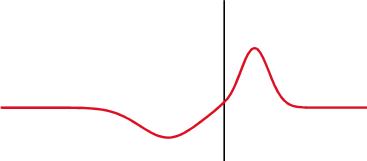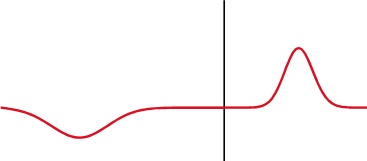
Partial Transmittance and Partial Reflectance: A wave experiences partial transmittance and partial reflectance when the medium through which it travels suddenly changes.

Superposition and Interference

A wave may have a complicated shape that can result from superposition and interference of several waves.

Most waves do not look very simple. They look are often more complex than the simple water waves often considered in textbooks. Simple waves may be created by a simple harmonic oscillation, and thus have a sinusoidal shape. Complex waves are more interesting, even beautiful, but they look formidable. Most waves appear complex because they result from several simple waves adding together. Luckily, the rules for adding waves are quite simple.

Complex Pattern of Waves: These waves result from the superposition of several waves from different sources, producing a complex pattern.

Superposition

When two or more waves arrive at the same point, they superimpose themselves on one another. More specifically, the disturbances of waves are superimposed when they come together—a phenomenon called superposition. Each disturbance corresponds to a force, and forces add. If the disturbances are along the same line, then the resulting wave is a simple addition of the disturbances of the individual waves—that is, their amplitudes add.

Interference

As a result of superposition of waves, interference can be observed. Interference is an effect caused by two or more waves.

When two identical waves arrive at the same point exactly in phase the crests of the two waves are precisely aligned, as are the troughs. This superposition produces pure constructive interference. Because the disturbances add, constructive interference may produce a wave that has twice the amplitude of the individual waves, but has the same wavelength.

Constructive Interference: Pure constructive interference of two identical waves produces one with twice the amplitude, but the same wavelength.

If two identical waves that arrive exactly out of phase—that is, precisely aligned crest to trough—they may produce pure destructive interference. Because the disturbances are in the opposite direction for this superposition, the resulting amplitude may be zero for destructive interference, and the waves completely cancel.

While pure constructive and pure destructive interference do occur, they require precisely aligned identical waves. The superposition of most waves produces a combination of constructive and destructive interference and can vary from place to place and time to time. Here again, the disturbances add and subtract, producing a more complicated looking wave.

Superposition of Non-Identical Waves: Superposition of non-identical waves exhibits both constructive and destructive interference.

Standing Waves and Resonance

A standing wave is one in which two waves superimpose to produce a wave that varies in amplitude but does not propagate.

Standing Wave

Sometimes waves do not seem to move, but rather they just vibrate in place. These waves are formed by the superposition of two or more moving waves for two identical waves moving in opposite directions. The waves move through each other with their disturbances adding as they go by. If the two waves have the same amplitude and wavelength then they alternate between constructive and destructive interference. The resultant looks like a wave standing in place and, thus, is called a standing wave.

Standing Wave: A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue).

Standing waves are found on the strings of musical instruments and are due to reflections of waves from the ends of the string. shows seven standing waves that can be created on a string that is fixed at both ends. Nodes are the points where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave. The fixed ends of strings must be nodes, too, because the string cannot move there. The word antinode is used to denote the location of maximum amplitude in standing waves. Standing waves on strings have a frequency that is related to the propagation speed v_w of the disturbance on the string. The wavelength λ is determined by the distance between the points where the string is fixed in place.

Standing Waves: Standing waves in a string, the fundamental mode and the first six overtones.

The lowest frequency, called the fundamental frequency, is thus for the longest wavelength, twice the length of the string. The overtones or harmonics are multiples of the fundamental frequency. shows the fundamental mode along with six overtones.

Resonance

A closer look at earthquakes provides evidence for conditions appropriate for resonance: standing waves, and constructive and destructive interference. A building may be vibrated for several seconds with a driving frequency matching that of the natural frequency of the vibration of the building—producing a resonance resulting in one building collapsing while neighboring buildings do not. Often buildings of a certain height are devastated while other taller buildings remain intact. The building height matches the condition for setting up a standing wave for that particular height. As the earthquake waves travel along the surface of Earth and reflect off denser rocks, constructive interference occurs at certain points. Often areas closer to the epicenter are not damaged while areas farther away are damaged.