Evaluate and Simplify Square Roots

Learning Objectives

  • Evaluate principal square roots
  • Use the product rule to simplify square roots

When the square root of a number is squared, the result is the original number. Since [latex]{4}^{2}=16[/latex], the square root of [latex]16[/latex] is [latex]4[/latex]. The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.

In general terms, if [latex]a[/latex] is a positive real number, then the square root of [latex]a[/latex] is a number that, when multiplied by itself, gives [latex]a[/latex]. The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals [latex]a[/latex]. The square root obtained using a calculator is the principal square root.

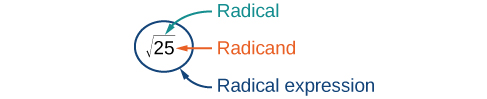
The principal square root of [latex]a[/latex] is written as [latex]\sqrt{a}[/latex]. The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.

The expression: square root of twenty-five is enclosed in a circle. The circle has an arrow pointing to it labeled: Radical expression. The square root symbol has an arrow pointing to it labeled: Radical. The number twenty-five has an arrow pointing to it labeled: Radicand.

A General Note: Principal Square Root

The principal square root of [latex]a[/latex] is the nonnegative number that, when multiplied by itself, equals [latex]a[/latex]. It is written as a radical expression, with a symbol called a radical over the term called the radicand: [latex]\sqrt{a}[/latex].

Q & A

Does [latex]\sqrt{25}=\pm 5[/latex]?

No. Although both [latex]{5}^{2}[/latex] and [latex]{\left(-5\right)}^{2}[/latex] are [latex]25[/latex], the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is [latex]\sqrt{25}=5[/latex].

Example: Evaluating Square Roots

Evaluate each expression.

  1. [latex]\sqrt{100}[/latex]
  2. [latex]\sqrt{\sqrt{16}}[/latex]
  3. [latex]\sqrt{25+144}[/latex]
  4. [latex]\sqrt{49}-\sqrt{81}[/latex]

Q & A

For [latex]\sqrt{25+144}[/latex], can we find the square roots before adding?

No. [latex]\sqrt{25}+\sqrt{144}=5+12=17[/latex]. This is not equivalent to [latex]\sqrt{25+144}=13[/latex]. The order of operations requires us to add the terms in the radicand before finding the square root.

Try It

Evaluate each expression.

  1. [latex]\sqrt{225}[/latex]
  2. [latex]\sqrt{\sqrt{81}}[/latex]
  3. [latex]\sqrt{25 - 9}[/latex]
  4. [latex]\sqrt{36}+\sqrt{121}[/latex]


Use the Product Rule to Simplify Square Roots

To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite [latex]\sqrt{15}[/latex] as [latex]\sqrt{3}\cdot \sqrt{5}[/latex]. We can also use the product rule to express the product of multiple radical expressions as a single radical expression.

A General Note: The Product Rule for Simplifying Square Roots

If [latex]a[/latex] and [latex]b[/latex] are nonnegative, the square root of the product [latex]ab[/latex] is equal to the product of the square roots of [latex]a[/latex] and [latex]b[/latex].

[latex]\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex]

How To: Given a square root radical expression, use the product rule to simplify it.

  1. Factor any perfect squares from the radicand.
  2. Write the radical expression as a product of radical expressions.
  3. Simplify.

Example: Using the Product Rule to Simplify Square Roots

Simplify the radical expression.

  1. [latex]\sqrt{300}[/latex]
  2. [latex]\sqrt{162{a}^{5}{b}^{4}}[/latex]

Try It

Simplify [latex]\sqrt{50{x}^{2}{y}^{3}z}[/latex].

How To: Given the product of multiple radical expressions, use the product rule to combine them into one radical expression.

  1. Express the product of multiple radical expressions as a single radical expression.
  2. Simplify.

Example: Using the Product Rule to Simplify the Product of Multiple Square Roots

Simplify the radical expression.

[latex]\sqrt{12}\cdot \sqrt{3}[/latex]

Try It

Simplify [latex]\sqrt{50x}\cdot \sqrt{2x}[/latex] assuming [latex]x>0[/latex].

Using the Quotient Rule to Simplify Square Roots

Just as we can rewrite the square root of a product as a product of square roots, so too can we rewrite the square root of a quotient as a quotient of square roots, using the quotient rule for simplifying square roots. It can be helpful to separate the numerator and denominator of a fraction under a radical so that we can take their square roots separately. We can rewrite [latex]\sqrt{\frac{5}{2}}[/latex] as [latex]\frac{\sqrt{5}}{\sqrt{2}}[/latex].

A General Note: The Quotient Rule for Simplifying Square Roots

The square root of the quotient [latex]\frac{a}{b}[/latex] is equal to the quotient of the square roots of [latex]a[/latex] and [latex]b[/latex], where [latex]b\ne 0[/latex].

[latex]\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}[/latex]

How To: Given a radical expression, use the quotient rule to simplify it.

  1. Write the radical expression as the quotient of two radical expressions.
  2. Simplify the numerator and denominator.

Example: Using the Quotient Rule to Simplify Square Roots

Simplify the radical expression.

[latex]\sqrt{\frac{5}{36}}[/latex]

Try It

Simplify [latex]\sqrt{\frac{2{x}^{2}}{9{y}^{4}}}[/latex].

Example: Using the Quotient Rule to Simplify an Expression with Two Square Roots

Simplify the radical expression.

[latex]\frac{\sqrt{234{x}^{11}y}}{\sqrt{26{x}^{7}y}}[/latex]

Try It

Simplify [latex]\frac{\sqrt{9{a}^{5}{b}^{14}}}{\sqrt{3{a}^{4}{b}^{5}}}[/latex].

In the following video you will see more examples of how to simplify radical expressions with variables.