Intercepts of Quadratic Functions

Learning Objectives

Find the y-intercept of a quadratic function
Find the real-number x-intercepts, or roots of a quadratic function using factoring and the quadratic formula

Much as we did in the application problems above, we also need to find intercepts of quadratic equations for graphing parabolas. Recall that we find the y-intercept of a quadratic by evaluating the function at an input of zero, and we find the x-intercepts at locations where the output is zero. Notice that the number of x-intercepts can vary depending upon the location of the graph.

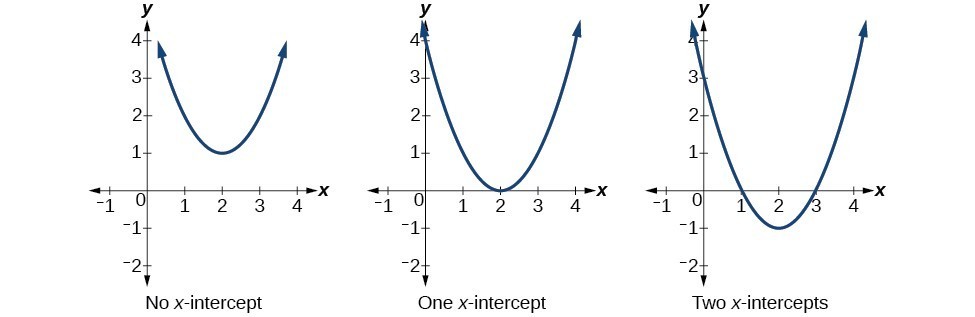
Three graphs where the first graph shows a parabola with no x-intercept, the second is a parabola with one –intercept, and the third parabola is of two x-intercepts.

Number of x-intercepts of a parabola

Mathematicians also define x-intercepts as roots of the quadratic function.

How To: Given a quadratic function $f\left(x\right)$ , find the y– and x-intercepts.

Evaluate $f\left(0\right)$ to find the y-intercept.
Solve the quadratic equation $f\left(x\right)=0$ to find the x-intercepts.

Example: Finding the y– and x-Intercepts of a Parabola

Find the y– and x-intercepts of the quadratic $f\left(x\right)=3{x}^{2}+5x - 2$ .

Solution

We find the y-intercept by evaluating

f (0)

$f\left(0\right)$ .

$\begin{array}{c}f\left(0\right)=3{\left(0\right)}^{2}+5\left(0\right)-2\hfill \\ \text{ }=-2\hfill \end{array}$

So the y-intercept is at $\left(0,-2\right)$ .

For the x-intercepts, or roots, we find all solutions of $f\left(x\right)=0$ .

$0=3{x}^{2}+5x - 2$

In this case, the quadratic can be factored easily, providing the simplest method for solution.

$0=\left(3x - 1\right)\left(x+2\right)$
$\begin{array}{c}0=3x - 1\hfill & \hfill & \hfill & \hfill & 0=x+2\hfill \\ x=\frac{1}{3}\hfill & \hfill & \text{or}\hfill & \hfill & x=-2\hfill \end{array}$

So the roots are at $\left(\frac{1}{3},0\right)$ and $\left(-2,0\right)$ .

Analysis of the Solution

By graphing the function, we can confirm that the graph crosses the y-axis at $\left(0,-2\right)$ . We can also confirm that the graph crosses the x-axis at $\left(\frac{1}{3},0\right)$ and $\left(-2,0\right)$ .

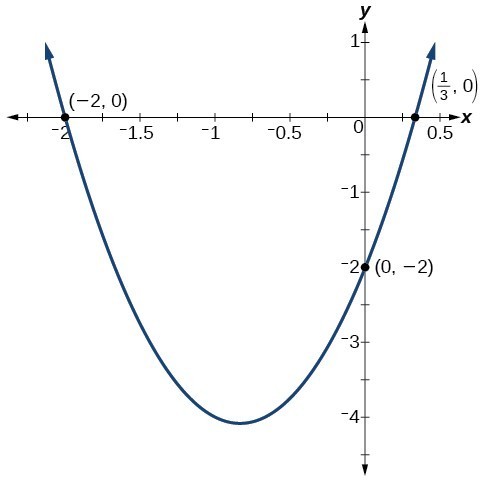
Graph of a parabola which has the following intercepts (-2, 0), (1/3, 0), and (0, -2).

In Example: Finding the y– and x-Intercepts of a Parabola, the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.

How To: Given a quadratic function, find the x-intercepts by rewriting in standard form.

Substitute a and b into $h=-\frac{b}{2a}$ .
Substitute x = h into the general form of the quadratic function to find k.
Rewrite the quadratic in standard form using h and k.
Solve for when the output of the function will be zero to find the x-intercepts.

Example: Finding the Roots of a Parabola

Find the x-intercepts of the quadratic function $f\left(x\right)=2{x}^{2}+4x - 4$ .

Solution

We begin by solving for when the output will be zero.

$0=2{x}^{2}+4x - 4$

Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.

$f\left(x\right)=a{\left(x-h\right)}^{2}+k$

We know that a = 2. Then we solve for h and k.

$\begin{array}{c}h=-\frac{b}{2a}\hfill & \hfill & \hfill & k=f\left(-1\right)\hfill \\ \text{ }=-\frac{4}{2\left(2\right)}\hfill & \hfill & \hfill & \text{ }=2{\left(-1\right)}^{2}+4\left(-1\right)-4\hfill \\ \text{ }=-1\hfill & \hfill & \hfill & \text{ }=-6\hfill \end{array}$

So now we can rewrite in standard form.

$f\left(x\right)=2{\left(x+1\right)}^{2}-6$

We can now solve for when the output will be zero.

$\begin{array}{c}0=2{\left(x+1\right)}^{2}-6\hfill \\ 6=2{\left(x+1\right)}^{2}\hfill \\ 3={\left(x+1\right)}^{2}\hfill \\ x+1=\pm \sqrt{3}\hfill \\ x=-1\pm \sqrt{3}\hfill \end{array}$

The graph has x-intercepts at $\left(-1-\sqrt{3},0\right)$ and $\left(-1+\sqrt{3},0\right)$ .

Analysis of the Solution

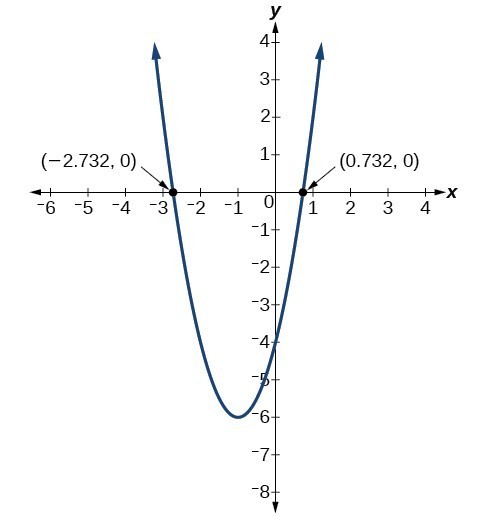
Graph of a parabola which has the following x-intercepts (-2.732, 0) and (0.732, 0).

We can check our work by graphing the given function on a graphing utility and observing the roots.

Try It

The function $g\left(x\right)=13+{x}^{2}-6x$ is graphed below. You can use Desmos to find the x-and y-intercepts by clicking on the graph. Four points will appear. List each point, and what kind of point it is, we got you started with the vertex:

Vertex = $(3,-16)$

https://www.desmos.com/calculator/ilnmrc6noz

Solution

Example: Solving a Quadratic Equation with the Quadratic Formula

Solve ${x}^{2}+x+2=0$ .

Solution

Let’s begin by writing the quadratic formula:

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

$x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}$ .

When applying the quadratic formula, we identify the coefficients a, b, and c. For the equation ${x}^{2}+x+2=0$ , we have a = 1, b = 1, and c = 2. Substituting these values into the formula we have:

$\begin{array}{c}x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}\hfill \\ \text{ }=\frac{-1\pm \sqrt{{1}^{2}-4\cdot 1\cdot \left(2\right)}}{2\cdot 1}\hfill \\ \text{ }=\frac{-1\pm \sqrt{1 - 8}}{2}\hfill \\ \text{ }=\frac{-1\pm \sqrt{-7}}{2}\hfill \\ \text{ }=\frac{-1\pm i\sqrt{7}}{2}\hfill \end{array}$

The solutions to the equation are $x=\frac{-1+i\sqrt{7}}{2}$ and $x=\frac{-1-i\sqrt{7}}{2}$ or $x=\frac{-1}{2}+\frac{i\sqrt{7}}{2}$ and $x=\frac{-1}{2}-\frac{i\sqrt{7}}{2}$ .

Example: Applying the Vertex and x-Intercepts of a Parabola

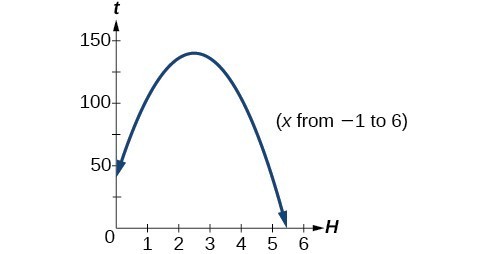
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation $H\left(t\right)=-16{t}^{2}+80t+40$ .

a. When does the ball reach the maximum height?

b. What is the maximum height of the ball?

c. When does the ball hit the ground?

Solution

a. The ball reaches the maximum height at the vertex of the parabola.

$\begin{array}{c} h=-\frac{80}{2\left(-16\right)} \text{ }=\frac{80}{32}\hfill \\ \text{ }=\frac{5}{2}\hfill \\ \text{ }=2.5\hfill \end{array}$

The ball reaches a maximum height after 2.5 seconds.

b. To find the maximum height, find the y coordinate of the vertex of the parabola.

$\begin{array}{c}k=H\left(-\frac{b}{2a}\right)\hfill \\ \text{ }=H\left(2.5\right)\hfill \\ \text{ }=-16{\left(2.5\right)}^{2}+80\left(2.5\right)+40\hfill \\ \text{ }=140\hfill \end{array}$

The ball reaches a maximum height of 140 feet.

c. To find when the ball hits the ground, we need to determine when the height is zero, $H\left(t\right)=0$ .

We use the quadratic formula.

$\begin{array}{c} t=\frac{-80\pm \sqrt{{80}^{2}-4\left(-16\right)\left(40\right)}}{2\left(-16\right)}\hfill \\ \text{ }=\frac{-80\pm \sqrt{8960}}{-32}\hfill \end{array}$

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

$\begin{array}{c}t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458\hfill & \text{or}\hfill & t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458\hfill \end{array}$

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

Graph of a negative parabola where x goes from -1 to 6.

Try It

A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation $H\left(t\right)=-16{t}^{2}+96t+112$ .

a. When does the rock reach the maximum height?

b. What is the maximum height of the rock?

c. When does the rock hit the ocean?

Solution

Quadratic Functions