Introduction to Equations of Lines

Learning Objectives

Equations of Lines

  • Write equations of lines in slope-intercept, point-slope, and standard forms
  • Identify the equations and graphs of horizontal and vertical lines
  • Determine whether two lines are parallel, perpendicular, or neither
  • Write equations of lines that are parallel or perpendicular to another line

Now that we’ve learned how to plot points on a coordinate plane and graph linear equations, we can begin to analyze the equations of lines and evaluate the different characteristics of these lines. In this section, we’ll learn about the commonly used forms for writing linear equations and the properties of lines that can be determined from their equations.

For example, without creating a table of values, you will be able to match each equation below to its corresponding graph. You will also be able to explain the similarities and differences of each line, how they relate to each other, and why they behave that way.

 

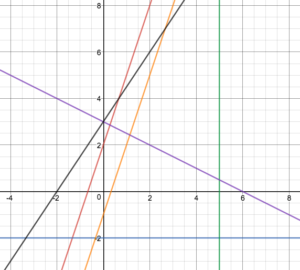
6 lines graphed on a coordinate plane.

(a) [latex]y=3x+2[/latex]

(b) [latex]y-4=-\frac{1}{2}(x+2)[/latex]

(c) [latex]x=5[/latex]

(d) [latex]y=-2[/latex]

(e) [latex]3x=y+1[/latex]

(f) [latex]2y-3x=6[/latex]