Learning Objectives
- Graph stretches and compressions of logarithmic functions
- Graph reflections of logarithmic functions
Graphing Stretches and Compressions of [latex]y=\text{log}_{b}\left(x\right)[/latex]
When the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] is multiplied by a constant a > 0, the result is a vertical stretch or compression of the original graph. To visualize stretches and compressions, we set a > 1 and observe the general graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] alongside the vertical stretch, [latex]g\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)[/latex] and the vertical compression, [latex]h\left(x\right)=\frac{1}{a}{\mathrm{log}}_{b}\left(x\right)[/latex].
try it
In the graph below, you can explore how to produce vertical stretches and compressions of a logarithmic function. The function [latex]g(x) = a\log_{b}{x}[/latex] represents a vertical stretch, and the function [latex]f(x) = \frac{1}{a}\log_{b}{x}[/latex] represents a vertical compression. As you investigate, consider the following questions;
- Both the vertical stretch and compression produce graphs that are increasing. Which transformation produces a function that increases faster?
- One of the key points that is commonly defined for transformations of a logarithmic function comes from finding the input that gives an output of [latex]y = 1[/latex]. This point can help you determine whether a graph is the result of a vertical compression or stretch. Explain why.
https://www.desmos.com/calculator/arlodqq7be
The still graphs below summarize the key features of the resulting graphs of vertical stretches and compressions of logarithmic functions.
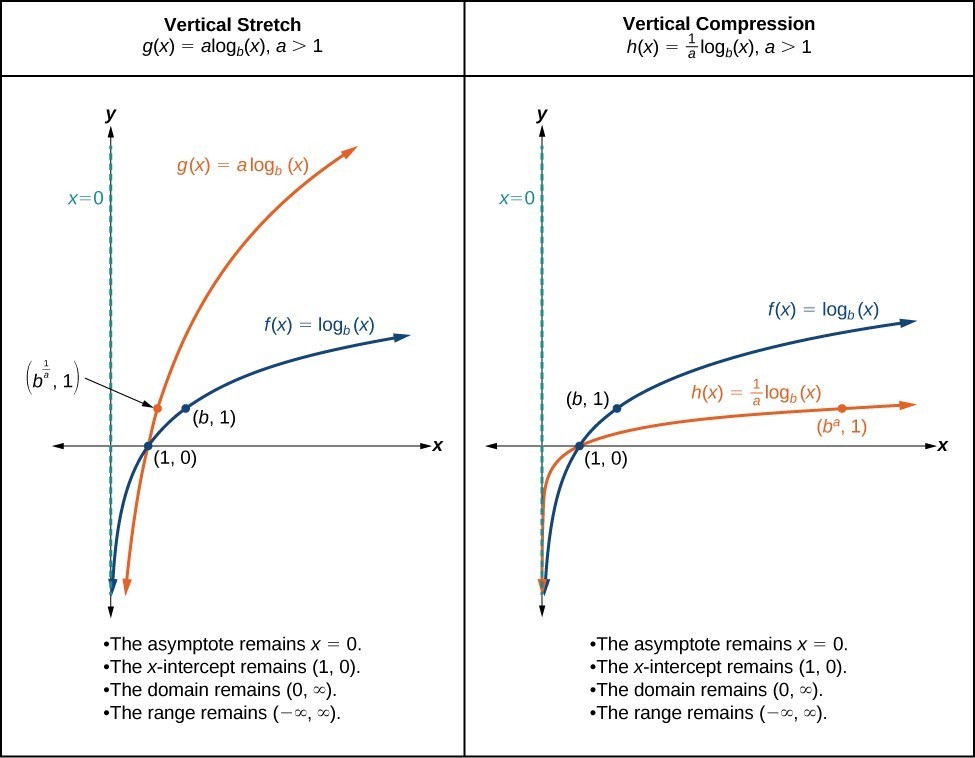
A General Note: Vertical Stretches and Compressions of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]
For any constant a > 1, the function [latex]f\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)[/latex]
- stretches the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] vertically by a factor of a if a > 1.
- compresses the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] vertically by a factor of a if 0 < a < 1.
- has the vertical asymptote x = 0.
- has the x-intercept [latex]\left(1,0\right)[/latex].
- has domain [latex]\left(0,\infty \right)[/latex].
- has range [latex]\left(-\infty ,\infty \right)[/latex].
How To: Given a logarithmic function with the form [latex]f\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)[/latex], [latex]a>0[/latex], graph the translation.
- Identify the vertical stretch or compressions:
- If [latex]|a|>1[/latex], the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] is stretched by a factor of a units.
- If [latex]|a|<1[/latex], the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] is compressed by a factor of a units.
- Draw the vertical asymptote x = 0.
- Identify three key points from the parent function. Find new coordinates for the shifted functions by multiplying the y coordinates by a.
- Label the three points.
- The domain is [latex]\left(0,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = 0.
Example: Graphing a Stretch or Compression of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]
Sketch a graph of [latex]f\left(x\right)=2{\mathrm{log}}_{4}\left(x\right)[/latex] alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Try It
Sketch a graph of [latex]f\left(x\right)=\frac{1}{2}{\mathrm{log}}_{4}\left(x\right)[/latex] alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Example: Combining a Shift and a Stretch
Sketch a graph of [latex]f\left(x\right)=5\mathrm{log}\left(x+2\right)[/latex]. State the domain, range, and asymptote.
Try It
Sketch a graph of the function [latex]f\left(x\right)=3\mathrm{log}\left(x - 2\right)+1[/latex]. State the domain, range, and asymptote.
Graphing Reflections of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]
When the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] is multiplied by –1, the result is a reflection about the x-axis. When the input is multiplied by –1, the result is a reflection about the y-axis. To visualize reflections, we restrict b > 1, and observe the general graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] alongside the reflection about the x-axis, [latex]g\left(x\right)={\mathrm{-log}}_{b}\left(x\right)[/latex] and the reflection about the y-axis, [latex]h\left(x\right)={\mathrm{log}}_{b}\left(-x\right)[/latex].
Try it
The functions [latex]f(x) = \log_{b}{x},g(x) = -\log_{b}{x}, h(x) = \log_{b}{-x} [/latex] are graphed below. The point of interest for the function [latex]f(x)[/latex] has also been added. Consider the following questions:
- Which graph, [latex]g(x) = -\log_{b}{x}, \text{ or }h(x) = \log_{b}{-x}[/latex] represents a vertical reflection? Which one represents a horizontal reflection?
- The point [latex](b,1)[/latex] has been added as a point of interest for the function [latex]f(x)[/latex]. Using the variable b as your x value, add the corresponding points of interest for [latex]g(x),\text{ and }h(x)[/latex].
- Does the vertical asymptote change when you reflect the graph of [latex]f(x)[/latex] either vertically or horizontally?
https://www.desmos.com/calculator/5qmaorrlst
The still graphs below summarize the key characteristics of reflecting [latex]f(x) = \log_{b}{x}[/latex] horizontally and vertically.

A General Note: Reflections of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]
The function [latex]f\left(x\right)={\mathrm{-log}}_{b}\left(x\right)[/latex]
- reflects the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] about the x-axis.
- has domain, [latex]\left(0,\infty \right)[/latex], range, [latex]\left(-\infty ,\infty \right)[/latex], and vertical asymptote, x = 0, which are unchanged from the parent function.
The function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(-x\right)[/latex]
- reflects the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] about the y-axis.
- has domain [latex]\left(-\infty ,0\right)[/latex].
- has range, [latex]\left(-\infty ,\infty \right)[/latex], and vertical asymptote, x = 0, which are unchanged from the parent function.
How To: Given a logarithmic function with the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex], graph a translation.
| [latex]\text{If }f\left(x\right)=-{\mathrm{log}}_{b}\left(x\right)[/latex] | [latex]\text{If }f\left(x\right)={\mathrm{log}}_{b}\left(-x\right)[/latex] |
|---|---|
| 1. Draw the vertical asymptote, x = 0. | 1. Draw the vertical asymptote, x = 0. |
| 2. Plot the x-intercept, [latex]\left(1,0\right)[/latex]. | 2. Plot the x-intercept, [latex]\left(1,0\right)[/latex]. |
| 3. Reflect the graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] about the x-axis. | 3. Reflect the graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] about the y-axis. |
| 4. Draw a smooth curve through the points. | 4. Draw a smooth curve through the points. |
| 5. State the domain, [latex]\left(0,\infty \right)[/latex], the range, [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote x = 0. | 5. State the domain, [latex]\left(-\infty ,0\right)[/latex], the range, [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote x = 0. |
Example: Graphing a Reflection of a Logarithmic Function
Sketch a graph of [latex]f\left(x\right)=\mathrm{log}\left(-x\right)[/latex] alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Try It
Graph [latex]f\left(x\right)=-\mathrm{log}\left(-x\right)[/latex]. State the domain, range, and asymptote.
How To: Given a logarithmic equation, use a graphing calculator to approximate solutions.
- Press [Y=]. Enter the given logarithm equation or equations as Y1= and, if needed, Y2=.
- Press [GRAPH] to observe the graphs of the curves and use [WINDOW] to find an appropriate view of the graphs, including their point(s) of intersection.
- To find the value of x, we compute the point of intersection. Press [2ND] then [CALC]. Select “intersect” and press [ENTER] three times. The point of intersection gives the value of x, for the point(s) of intersection.
Example: Approximating the Solution of a Logarithmic Equation
Solve [latex]4\mathrm{ln}\left(x\right)+1=-2\mathrm{ln}\left(x - 1\right)[/latex] graphically. Round to the nearest thousandth.
Try It
Solve [latex]5\mathrm{log}\left(x+2\right)=4-\mathrm{log}\left(x\right)[/latex] graphically. Round to the nearest thousandth.
Summarizing Translations of the Logarithmic Function
Now that we have worked with each type of translation for the logarithmic function, we can summarize each in the table below to arrive at the general equation for translating exponential functions.
| Translations of the Parent Function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] | |
|---|---|
| Translation | Form |
Shift
|
[latex]y={\mathrm{log}}_{b}\left(x+c\right)+d[/latex] |
Stretch and Compress
|
[latex]y=a{\mathrm{log}}_{b}\left(x\right)[/latex] |
| Reflect about the x-axis | [latex]y=-{\mathrm{log}}_{b}\left(x\right)[/latex] |
| Reflect about the y-axis | [latex]y={\mathrm{log}}_{b}\left(-x\right)[/latex] |
| General equation for all translations | [latex]y=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex] |
A General Note: Translations of Logarithmic Functions
All translations of the parent logarithmic function, [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex], have the form
[latex] f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex]
where the parent function, [latex]y={\mathrm{log}}_{b}\left(x\right),b>1[/latex], is
- shifted vertically up d units.
- shifted horizontally to the left c units.
- stretched vertically by a factor of |a| if |a| > 0.
- compressed vertically by a factor of |a| if 0 < |a| < 1.
- reflected about the x-axis when a < 0.
For [latex]f\left(x\right)=\mathrm{log}\left(-x\right)[/latex], the graph of the parent function is reflected about the y-axis.
Example: Finding the Vertical Asymptote of a Logarithm Graph
What is the vertical asymptote of [latex]f\left(x\right)=-2{\mathrm{log}}_{3}\left(x+4\right)+5[/latex]?
Try It
What is the vertical asymptote of [latex]f\left(x\right)=3+\mathrm{ln}\left(x - 1\right)[/latex]?
Example: Finding the Equation from a Graph
Find a possible equation for the common logarithmic function graphed below.

Try It
Give the equation of the natural logarithm graphed below.

Q & A
Is it possible to tell the domain and range and describe the end behavior of a function just by looking at the graph?
Yes, if we know the function is a general logarithmic function. For example, look at the graph in the last Try It. The graph approaches x = –3 (or thereabouts) more and more closely, so x = –3 is, or is very close to, the vertical asymptote. It approaches from the right, so the domain is all points to the right, [latex]\left\{x|x>-3\right\}[/latex]. The range, as with all general logarithmic functions, is all real numbers. And we can see the end behavior because the graph goes down as it goes left and up as it goes right. The end behavior is that as [latex]x\to -{3}^{+},f\left(x\right)\to -\infty [/latex] and as [latex]x\to \infty ,f\left(x\right)\to \infty [/latex].





