In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.

Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section we will learn techniques for solving exponential and logarithmic equations.

Exponential Equations

The first technique we will introduce for solving exponential equations involves using the definition of the logarithm.

Logarithmic Equations

We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] is equal to the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

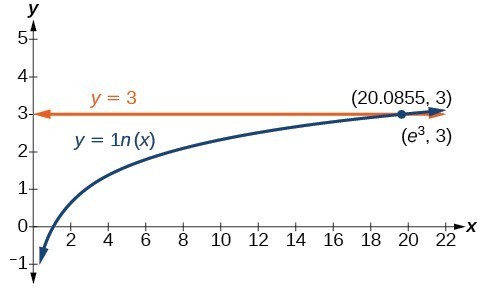
Example: Using a Graph to Understand the Solution to a Logarithmic Equation

Solve [latex]\mathrm{ln}x=3[/latex].

Show Solution

[latex]\begin{array}{l}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of }\mathrm{ln}\text{.}\hfill \end{array}[/latex]

Below is a graph of the equation. On the graph the x-coordinate of the point where the two graphs intersect is close to 20. In other words [latex]{e}^{3}\approx 20[/latex]. A calculator gives a better approximation: [latex]{e}^{3}\approx 20.0855[/latex].

The graphs of [latex]y=\mathrm{ln}x[/latex] and y = 3 cross at the point [latex]\left(e^3,3\right)[/latex] which is approximately (20.0855, 3).

Change-of-Base Formula for Logarithms

Some calculators can only evaluate common and natural logs. In order to evaluate logarithms with a base other than 10 or [latex]e[/latex], we use the change-of-base formula to rewrite the logarithm as the quotient of logarithms of any other base; when using a calculator, we would change them to common or natural logs.

To derive the change-of-base formula, we use the one-to-one property and power rule for logarithms.

Given any positive real numbers M, b, and n, where [latex]n\ne 1[/latex] and [latex]b\ne 1[/latex], we show

[latex]{\mathrm{log}}_{b}M\text{=}\frac{{\mathrm{log}}_{n}M}{{\mathrm{log}}_{n}b}[/latex]

Let [latex]y={\mathrm{log}}_{b}M[/latex]. Converting to exponential form, we obtain [latex]{b}^{y}=M[/latex]. It follows that:

[latex]\begin{array}{l}{\mathrm{log}}_{n}\left({b}^{y}\right)\hfill & ={\mathrm{log}}_{n}M\hfill & \text{Apply the one-to-one property}.\hfill \\ y{\mathrm{log}}_{n}b\hfill & ={\mathrm{log}}_{n}M \hfill & \text{Apply the power rule for logarithms}.\hfill \\ y\hfill & =\frac{{\mathrm{log}}_{n}M}{{\mathrm{log}}_{n}b}\hfill & \text{Isolate }y.\hfill \\ {\mathrm{log}}_{b}M\hfill & =\frac{{\mathrm{log}}_{n}M}{{\mathrm{log}}_{n}b}\hfill & \text{Substitute for }y.\hfill \end{array}[/latex]

For example, to evaluate [latex]{\mathrm{log}}_{5}36[/latex] using a calculator, we must first rewrite the expression as a quotient of common or natural logs. We will use the common log.

[latex]\begin{array}{l}{\mathrm{log}}_{5}36\hfill & =\frac{\mathrm{log}\left(36\right)}{\mathrm{log}\left(5\right)}\hfill & \text{Apply the change of base formula using base 10}\text{.}\hfill \\ \hfill & \approx 2.2266\text{ }\hfill & \text{Use a calculator to evaluate to 4 decimal places}\text{.}\hfill \end{array}[/latex]

Using a Graph to Approximate a Solution to an Exponential Equation

Graphing can help you confirm or find the solution to an exponential equation. For example,[latex]42=1.2{\left(5\right)}^{x}+2.8[/latex] can be solved to find the specific value for x that makes it a true statement. Graphing [latex]y=4[/latex] along with [latex]y=2^{x}[/latex] in the same window, the point(s) of intersection if any represent the solutions of the equation.

To use a calculator to solve this, press [Y=] and enter [latex]1.2(5)x+2.8[/latex] next to Y1=. Then enter 42 next to Y2=. For a window, use the values –3 to 3 for[latex]x[/latex] and –5 to 55 for[latex]y[/latex].Press [GRAPH]. The graphs should intersect somewhere near[latex]x=2[/latex].

For a better approximation, press [2ND] then [CALC]. Select [5: intersect] and press [ENTER] three times. The x-coordinate of the point of intersection is displayed as 2.1661943. (Your answer may be different if you use a different window or use a different value for Guess?) To the nearest thousandth,x≈2.166.

Using a Graph to Approximate a Solution to a Logarithmic Equation

How To: Given a logarithmic equation, use a graphing calculator to approximate solutions

1. Press [Y=]. Enter the given logarithmic equation or equations as Y₁= and, if needed, Y₂=.
2. Press [GRAPH] to observe the graphs of the curves and use [WINDOW] to find an appropriate view of the graphs, including their point(s) of intersection.
3. To find the value of x, we compute the point of intersection. Press [2ND] then [CALC]. Select “intersect” and press [ENTER] three times. The point of intersection gives the value of x for the point(s) of intersection.

Example: Approximating the Solution of a Logarithmic Equation

Solve [latex]4\mathrm{ln}\left(x\right)+1=-2\mathrm{ln}\left(x - 1\right)[/latex] graphically. Round to the nearest thousandth.

Key Concepts

• When given an equation of the form [latex]{\mathrm{log}}_{b}\left(S\right)=c[/latex], where S is an algebraic expression, we can use the definition of a logarithm to rewrite the equation as the equivalent exponential equation [latex]{b}^{c}=S[/latex] and solve for the unknown.
• A graphing calculator may be used to approximate solutions to some exponential and logarithmic equations.
• We can also use graphing to solve equations of the form [latex]{\mathrm{log}}_{b}\left(S\right)=c[/latex]. We graph both equations [latex]y={\mathrm{log}}_{b}\left(S\right)[/latex] and [latex]y=c[/latex] on the same coordinate plane and identify the solution as the x-value of the point of intersecting.
• Combining the skills learned in this and previous sections, we can solve equations that model real world situations whether the unknown is in an exponent or in the argument of a logarithm.

Glossary

change-of-base formula

a formula for converting a logarithm with any base to a quotient of logarithms with any other base