Graphs of Linear Functions

Learning Outcomes

  • Graph linear functions by plotting points, using the slope and y-intercept, and using transformations.(CLO #1, #3, #6)
  • Write the equation of a linear function given its graph. (CLO #1, #3, #6)
  • Match linear functions with their graphs. (CLO #1, #3, #6)
  • Find the x-intercept of a function given its equation. (CLO #1, #3, #6)
  • Find the equations of vertical and horizontal lines. (CLO #1, #3, #6)

We can now describe a variety of characteristics that explain the behavior of linear functions. We will use this information to analyze a graphed line and write an equation based on its observable properties. From evaluating the graph, what can you determine about this linear function?

Graph of the function f(x)= frac {2}{3} x plus 1

  • initial value (y-intercept)?
  • one or two points?
  • slope?
  • increasing or decreasing?
  • vertical or horizontal?

In this section, you will practice writing linear function equations using the information you’ve gathered. We will also practice graphing linear functions using different methods and predict how the graphs of linear functions will change when parts of the equation are altered.

[latex]\\[/latex]

Graphing Linear Functions

We previously saw that that the graph of a linear function is a straight line. We were also able to see the points of the function as well as the initial value from a graph.

There are three basic methods of graphing linear functions. The first is by plotting points and then drawing a line through the points. The second is by using the y-intercept and slope. The third is applying transformations to the identity function [latex]f\left(x\right)=x[/latex].

Graphing a Function by Plotting Points

To find points of a function, we can choose input values, evaluate the function at these input values, and calculate output values. The input values and corresponding output values form coordinate pairs. We then plot the coordinate pairs on a grid. In general we should evaluate the function at a minimum of two inputs in order to find at least two points on the graph of the function. For example, given the function [latex]f\left(x\right)=2x[/latex], we might use the input values 1 and 2. Evaluating the function for an input value of 1 yields an output value of 2 which is represented by the point (1, 2). Evaluating the function for an input value of 2 yields an output value of 4 which is represented by the point (2, 4). Choosing three points is often advisable because if all three points do not fall on the same line, we know we made an error.

How To: Given a linear function, graph by plotting points.

  1. Choose a minimum of two input values.
  2. Evaluate the function at each input value.
  3. Use the resulting output values to identify coordinate pairs.
  4. Plot the coordinate pairs on a grid.
  5. Draw a line through the points.

Example: Graphing by Plotting Points

Graph [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex] by plotting points.

Try It

Graph [latex]f\left(x\right)=-\frac{3}{4}x+6[/latex] by plotting points.

Graphing a Linear Function Using y-intercept and Slope

Another way to graph linear functions is by using specific characteristics of the function rather than plotting points. The first characteristic is its y-intercept which is the point at which the input value is zero. To find the y-intercept, we can set [latex]x=0[/latex] in the equation.

The other characteristic of the linear function is its slope, m, which is a measure of its steepness. Recall that the slope is the rate of change of the function. The slope of a linear function is equal to the ratio of the change in outputs to the change in inputs. Another way to think about the slope is by dividing the vertical difference, or rise, between any two points by the horizontal difference, or run. The slope of a linear function will be the same between any two points. We encountered both the y-intercept and the slope in Linear Functions.

Let’s consider the following function.

[latex]f\left(x\right)=\frac{1}{2}x+1[/latex]

The slope is [latex]\frac{1}{2}[/latex]. Because the slope is positive, we know the graph will slant upward from left to right. The y-intercept is the point on the graph when x = 0. The graph crosses the y-axis at (0, 1). Now we know the slope and the y-intercept. We can begin graphing by plotting the point (0, 1) We know that the slope is rise over run, [latex]m=\frac{\text{rise}}{\text{run}}[/latex]. From our example, we have [latex]m=\frac{1}{2}[/latex], which means that the rise is 1 and the run is 2. Starting from our y-intercept (0, 1), we can rise 1 and then run 2 or run 2 and then rise 1. We repeat until we have multiple points, and then we draw a line through the points as shown below.

graph of the line y = (1/2)x +1 showing the "rise", or change in the y direction as 1 and the "run", or change in x direction as 2, and the y-intercept at (0,1)

A General Note: Graphical Interpretation of a Linear Function

In the equation [latex]f\left(x\right)=mx+b[/latex]

  • b is the y-intercept of the graph and indicates the point (0, b) at which the graph crosses the y-axis.
  • m is the slope of the line and indicates the vertical displacement (rise) and horizontal displacement (run) between each successive pair of points. Recall the formula for the slope:

[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Q & A

Do all linear functions have y-intercepts?

Yes. All linear functions cross the y-axis and therefore have y-intercepts. (Note: A vertical line parallel to the y-axis does not have a y-intercept. Keep in mind that a vertical line is the only line that is not a function.)

How To: Given the equation for a linear function, graph the function using the y-intercept and slope.

  1. Evaluate the function at an input value of zero to find the y-intercept.
  2. Identify the slope.
  3. Plot the point represented by the y-intercept.
  4. Use [latex]\frac{\text{rise}}{\text{run}}[/latex] to determine at least two more points on the line.
  5. Draw a line which passes through the points.

Example: Graphing by Using the y-intercept and Slope

Graph [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex] using the y-intercept and slope.

Try It

Find a point on the graph we drew in the previous example: Graphing by Using the y-intercept and Slope that has a negative x-value.

Graphing a Linear Function Using Transformations

Another option for graphing is to use transformations on the identity function [latex]f\left(x\right)=x[/latex]. A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.

Vertical Stretch or Compression

In the equation [latex]f\left(x\right)=mx[/latex], the m is acting as the vertical stretch or compression of the identity function. When m is negative, there is also a vertical reflection of the graph. Notice that multiplying the equation [latex]f\left(x\right)=x[/latex] by m stretches the graph of f by a factor of m units if m > 1 and compresses the graph of f by a factor of m units if 0 < m < 1. This means the larger the absolute value of m, the steeper the slope.

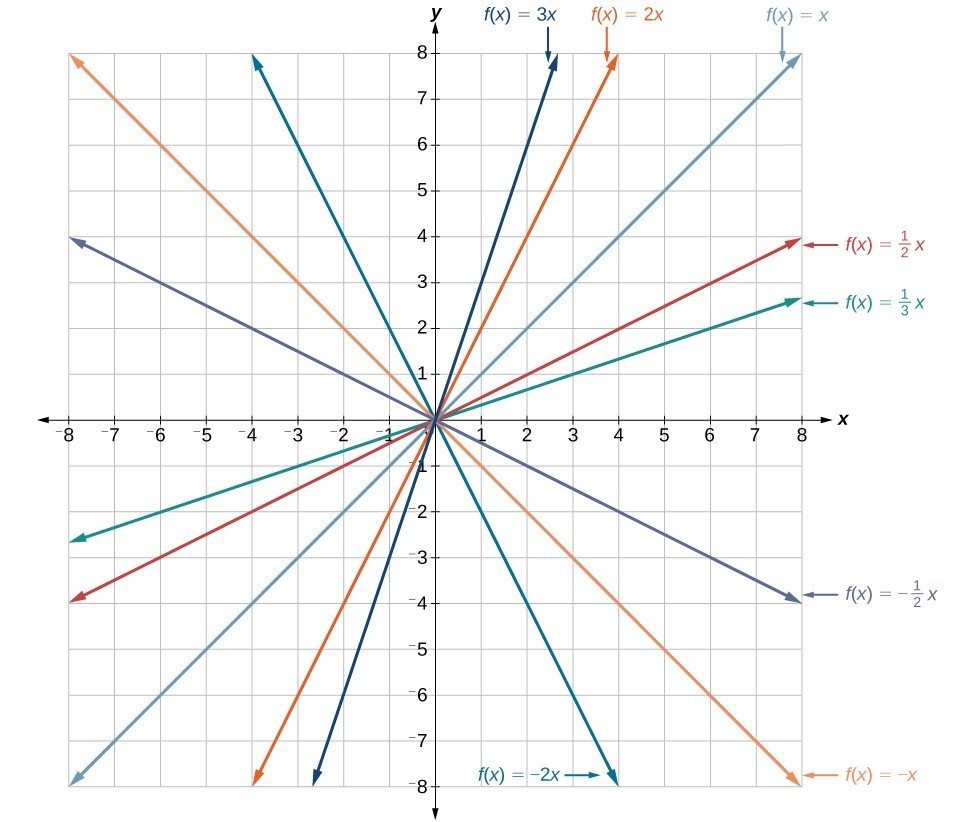
Graph with several linear functions including y = 3x, y = 2x, y = x, y = (1/2)x, y = (1/3)x, y = (-1/2)x, y = -x, and y = -2x

Vertical stretches and compressions and reflections on the function [latex]f\left(x\right)=x[/latex].

Vertical Shift

In [latex]f\left(x\right)=mx+b[/latex], the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice that adding a value of b to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of f a total of b units up if b is positive and |b| units down if b is negative.

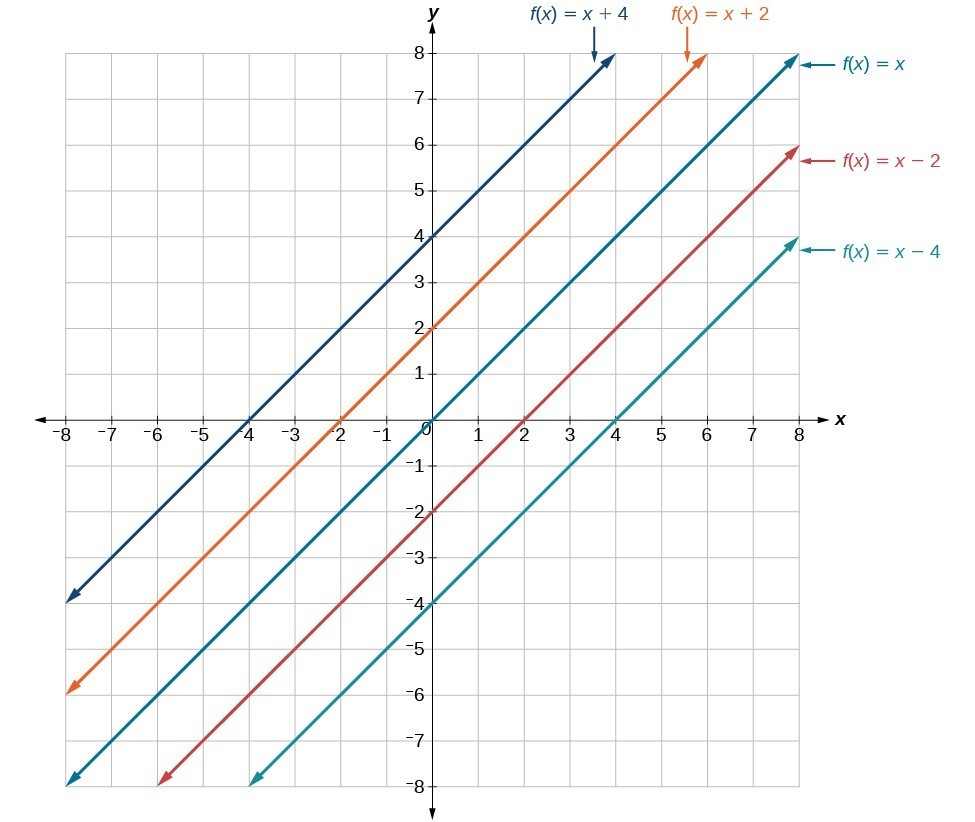
graph showing y = x , y = x+2, y = x+4, y = x-2, y = x-4

This graph illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].

Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.

Here is a video showing how to graph a linear function using transformations on the graph of the identity function f(x) = x.  Graphing a Linear Function Using Transformations on the graph of f(x) = x

How To: Given the equation of a linear function, use transformations to graph the linear function in the form [latex]f\left(x\right)=mx+b[/latex].

  1. Graph [latex]f\left(x\right)=x[/latex].
  2. Vertically stretch or compress the graph by a factor m.
  3. Shift the graph up or down b units.

Example: Graphing by Using Transformations

Graph [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex] using transformations.

Try It

Graph [latex]f\left(x\right)=4+2x[/latex], using transformations.


Q & A

In Example: Graphing by Using Transformations, could we have sketched the graph by reversing the order of the transformations?

No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first. For example, following order of operations, let the input be 2.

[latex]\begin{array}{l}f\text{(2)}=\frac{\text{1}}{\text{2}}\text{(2)}-\text{3}\hfill \\ =\text{1}-\text{3}\hfill \\ =-\text{2}\hfill \end{array}[/latex]

Writing Equations of Linear Functions

We previously wrote the equation for a linear function from a graph. Now we can extend what we know about graphing linear functions to analyze graphs a little more closely. Begin by taking a look at the graph below. We can see right away that the graph crosses the y-axis at the point (0, 4), so this is the y-intercept.

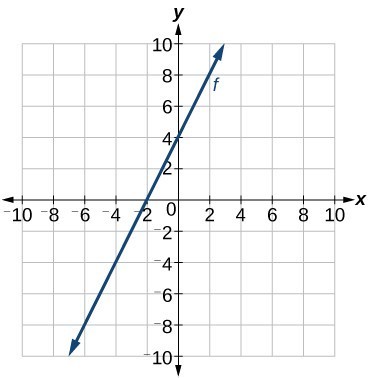
image

Then we can calculate the slope by finding the rise and run. We can choose any two points, but let’s look at the point (–2, 0). To get from this point to the y-intercept, we must move up 4 units (rise) and to the right 2 units (run). So the slope must be:

[latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{2}=2[/latex]

Substituting the slope and y-intercept into slope-intercept form of a line gives:

[latex]y=2x+4[/latex]

Here is a video showing how to find the equation of a line using the graph of the line.  Find the equation of the line given the graph

How To: Given THE graph of A linear function, find the equation to describe the function.

  1. Identify the y-intercept from the graph.
  2. Choose two points to determine the slope.
  3. Substitute the y-intercept and slope into slope-intercept form of a line.

Example: Matching Linear Functions to Their Graphs

Match each equation of a linear function with one of the lines in the graph below.

  1. [latex]f\left(x\right)=2x+3[/latex]
  2. [latex]g\left(x\right)=2x - 3[/latex]
  3. [latex]h\left(x\right)=-2x+3[/latex]
  4. [latex]j\left(x\right)=\frac{1}{2}x+3[/latex]

Graph of three lines, line 1) passes through (0,3) and (-2, -1), line 2) passes through (0,3) and (-6,0), line 3) passes through (0,-3) and (2,1)

Try It

Finding the x-intercept of a Line

So far we have been finding the y-intercepts of functions: the point at which the graph of a function crosses the y-axis. A function may also have an x-intercept, which is the x-coordinate of the point where the graph of a function crosses the x-axis. In other words, it is the input value when the output value is zero.

To find the x-intercept, set the function f(x) equal to zero and solve for the value of x. For example, consider the function shown:

[latex]f\left(x\right)=3x - 6[/latex]

Set the function equal to 0 and solve for x.

[latex]\begin{array}{l}0=3x - 6\hfill \\ 6=3x\hfill \\ 2=x\hfill \\ x=2\hfill \end{array}[/latex]

The graph of the function crosses the x-axis at the point (2, 0).

Q & A

Do all linear functions have x-intercepts?

No. However, linear functions of the form y = c, where c is a nonzero real number are the only examples of linear functions with no x-intercept. For example, y = 5 is a horizontal line 5 units above the x-axis. This function has no x-intercepts.

Graph of y = 5.

A General Note: x-intercept

The x-intercept of a function is the value of x where f(x) = 0. It can be found by solving the equation 0 = mx + b.

Example: Finding an x-intercept

Find the x-intercept of [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex].

Try It

Find the x-intercept of [latex]f\left(x\right)=\frac{1}{4}x - 4[/latex].

Describing Horizontal and Vertical Lines

There are two special cases of lines on a graph—horizontal and vertical lines. A horizontal line indicates a constant output or y-value. In the graph below, we see that the output has a value of 2 for every input value. The change in outputs between any two points is 0. In the slope formula, the numerator is 0, so the slope is 0. If we use m = 0 in the equation [latex]f\left(x\right)=mx+b[/latex], the equation simplifies to [latex]f\left(x\right)=b[/latex]. In other words, the value of the function is a constant. This graph represents the function [latex]f\left(x\right)=2[/latex].

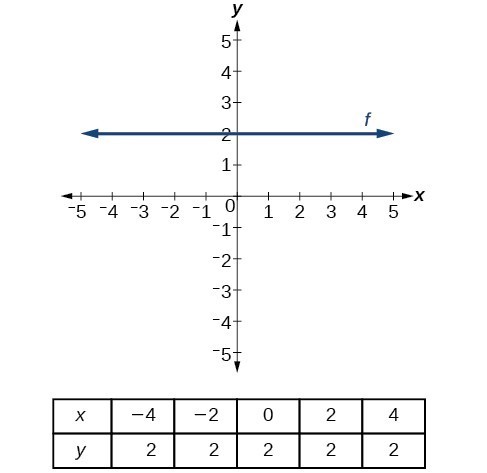
image

A horizontal line representing the function [latex]f\left(x\right)=2[/latex].

 

M equals change of output divided by change of input. The numerator is a non-zero real number, and the change of input is zero.

A vertical line indicates a constant input or x-value. We can see that the input value for every point on the line is 2, but the output value varies. Because this input value is mapped to more than one output value, a vertical line does not represent a function. Notice that between any two points, the change in the input values is zero. In the slope formula, the denominator will be zero, so the slope of a vertical line is undefined.

Notice that a vertical line has an x-intercept but no y-intercept unless it’s the line x = 0. This graph represents the line x = 2.

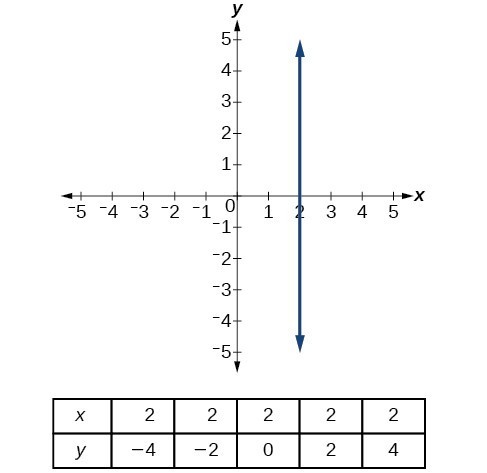
image

The vertical line [latex]x=2[/latex] which does not represent a function.

A General Note: Horizontal and Vertical Lines

Lines can be horizontal or vertical.

A horizontal line is a line defined by an equation of the form [latex]f\left(x\right)=b[/latex] where [latex]b[/latex] is a constant.

A vertical line is a line defined by an equation of the form [latex]x=a[/latex] where [latex]a[/latex] is a constant.

Example: Writing the Equation of a Horizontal Line

Write the equation of the line graphed below.

Graph of x = 7.

Try it

 

Example: Writing the Equation of a Vertical Line

Write the equation of the line graphed below.

Graph of two functions where the baby blue line is y = -2/3x + 7, and the blue line is y = -x + 1.

Try It

Try It

  • Write the equation of the function passing through the points [latex](2,6)[/latex] and [latex](4,4)[/latex] in slope-intercept form.
  • Write the equation of a function whose slope is 2 and passes through the point [latex](-1,0)[/latex]
  • Write the equation of a function whose slope is undefined.

Solutions:  y = -x + 8,  y = 2x + 2,   x = 4 (this could be any number – vertical lines have undefined slopes)

Key Concepts

  • Linear functions may be graphed by plotting points or by using the y-intercept and slope.
  • Graphs of linear functions may be transformed by shifting the graph up, down, left, or right as well as using stretches, compressions, and reflections.
  • The y-intercept and slope of a line may be used to write the equation of a line.
  • The x-intercept is the point at which the graph of a linear function crosses the x-axis.
  • Horizontal lines are written in the form, [latex]f(x)=b[/latex].
  • Vertical lines are written in the form, [latex]x=b[/latex].

Glossary

horizontal line
a line defined by [latex]f\left(x\right)=b[/latex] where b is a real number. The slope of a horizontal line is 0.
vertical line
a line defined by [latex]x=a[/latex] where a is a real number. The slope of a vertical line is undefined.
x-intercept
the point on the graph of a linear function when the output value is 0; the point at which the graph crosses the horizontal axis