In 2010, a major earthquake struck Haiti destroying or damaging over 285,000 homes.[1] One year later, another, stronger earthquake devastated Honshu, Japan destroying or damaging over 332,000 buildings[2] like those shown in the picture below. Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale[3] whereas the Japanese earthquake registered a 9.0.[4]

Devastation of March 11, 2011 earthquake in Honshu, Japan. (credit: Daniel Pierce)
The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude 8 is not twice as great as an earthquake of magnitude 4. It is [latex]{10}^{8 - 4}={10}^{4}=10,000[/latex] times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake was 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is [latex]{10}^{x}=500[/latex] where x represents the difference in magnitudes on the Richter Scale. How would we solve for x?
We have not yet learned a method for solving exponential equations algebraically. None of the algebraic tools discussed so far is sufficient to solve [latex]{10}^{x}=500[/latex]. We know that [latex]{10}^{2}=100[/latex] and [latex]{10}^{3}=1000[/latex], so it is clear that x must be some value between 2 and 3 since [latex]y={10}^{x}[/latex] is increasing. We can examine a graph to better estimate the solution.
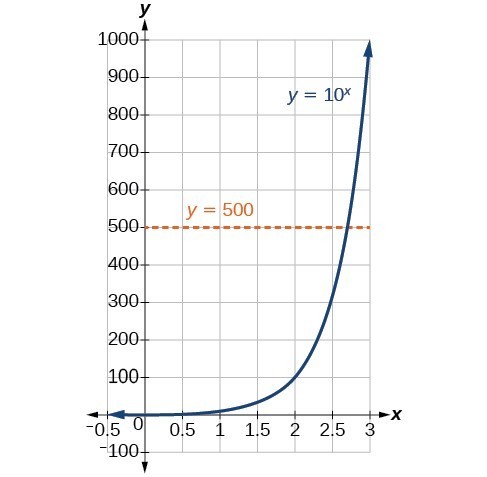
Estimating from a graph, however, is imprecise. To find an algebraic solution, we must introduce a new function.
Previously, we saw how creating a graphical representation of an exponential model gives us another layer of insight for predicting future events. How do logarithmic graphs give us insight into situations? Because every logarithmic function is the inverse function of an exponential function, we can think of every output on a logarithmic graph as the input for the corresponding inverse exponential equation. In other words, logarithms give the cause for an effect.
To illustrate, suppose we invest $2500 in an account that offers an annual interest rate of 5% compounded continuously. We already know that the balance in our account for any year t can be found with the equation [latex]A=2500{e}^{0.05t}[/latex].
What if we wanted to know the year for any balance? We would need to create a corresponding new function by interchanging the input and the output; thus we would need to create a logarithmic model for this situation. By graphing the model, we can see the output (year) for any input (account balance). For instance, what if we wanted to know how many years it would take for our initial investment to double? The graph below shows this point.

Key Equations
| Definition of the logarithmic function | For [latex]\text{ } x>0,b>0,b\ne 1[/latex], [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] if and only if [latex]\text{ }{b}^{y}=x[/latex]. |
| Definition of the common logarithm | For [latex]\text{ }x>0[/latex], [latex]y=\mathrm{log}\left(x\right)[/latex] if and only if [latex]\text{ }{10}^{y}=x[/latex]. |
| Definition of the natural logarithm | For [latex]\text{ }x>0[/latex], [latex]y=\mathrm{ln}\left(x\right)[/latex] if and only if [latex]\text{ }{e}^{y}=x[/latex]. |
| General Form for the Transformation of the Parent Logarithmic Function [latex]\text{ }f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] | [latex]f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex] |
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/#summary. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#summary. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#details. Accessed 3/4/2013. ↵