Learning Outcomes
- Convert a fraction to a decimal
- Identify a fraction whose decimal form is repeating
- Add a fraction and decimal by converting between forms
In Decimals, we learned to convert decimals to fractions. Now we will do the reverse—convert fractions to decimals. Remember that the fraction bar indicates division. So [latex]{\Large\frac{4}{5}}[/latex] can be written [latex]4\div 5[/latex] or [latex]5\overline{)4}[/latex]. This means that we can convert a fraction to a decimal by treating it as a division problem.
Convert a Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
example
Write the fraction [latex]{\Large\frac{3}{4}}[/latex] as a decimal.
Solution
| A fraction bar means division, so we can write the fraction [latex]\Large\frac{3}{4}[/latex] using division. |  |
| Divide. |  |
| So the fraction [latex]{\Large\frac{3}{4}}[/latex] is equal to [latex]0.75[/latex]. |
try it
The following video contains an example of how to write a fraction as a decimal.
example
Write the fraction [latex]-{\Large\frac{7}{2}}[/latex] as a decimal.
try it
Repeating Decimals
So far, in all the examples converting fractions to decimals the division resulted in a remainder of zero. This is not always the case. Let’s see what happens when we convert the fraction [latex]{\Large\frac{4}{3}}[/latex] to a decimal. First, notice that [latex]{\Large\frac{4}{3}}[/latex] is an improper fraction. Its value is greater than [latex]1[/latex]. The equivalent decimal will also be greater than [latex]1[/latex].
We divide [latex]4[/latex] by [latex]3[/latex].
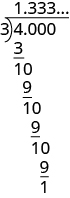
No matter how many more zeros we write, there will always be a remainder of [latex]1[/latex], and the threes in the quotient will go on forever. The number [latex]\text{1.333}\dots [/latex] is called a repeating decimal. Remember that the “…” means that the pattern repeats.
Repeating Decimal
A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.
How do you know how many ‘repeats’ to write? Instead of writing [latex]1.333\dots [/latex] we use a shorthand notation by placing a line over the digits that repeat. The repeating decimal [latex]1.333\dots [/latex] is written [latex]1.\overline{3}[/latex]. The line above the [latex]3[/latex] tells you that the [latex]3[/latex] repeats endlessly. So [latex]\text{1.333}\dots=1.\overline{3}[/latex]
For other decimals, two or more digits might repeat. The table below shows some more examples of repeating decimals.
| [latex]\text{1.333}\ldots=1.\overline{3}[/latex] | [latex]3[/latex] is the repeating digit |
| [latex]\text{4.1666}\ldots=4.1\overline{6}[/latex] | [latex]6[/latex] is the repeating digit |
| [latex]\text{4.161616}\ldots=4.\overline{16}[/latex] | [latex]16[/latex] is the repeating block |
| [latex]\text{0.271271271}\ldots =0.\overline{271}[/latex] | [latex]271[/latex] is the repeating block |
example
Write [latex]{\Large\frac{43}{22}}[/latex] as a decimal.
try it
The next video example shows an example of converting fractions to decimals when the result is repeating.
It is useful to convert between fractions and decimals when we need to add or subtract numbers in different forms. To add a fraction and a decimal, for example, we would need to either convert the fraction to a decimal or the decimal to a fraction.
example
Simplify: [latex]{\Large\frac{7}{8}}+6.4[/latex]
