Fractal Dimension

Learning Outcomes

  • Scale a geometric object by a specific scaling factor using the scaling dimension relation
  • Determine the fractal dimension of a fractal object

In addition to visual self-similarity, fractals exhibit other interesting properties. For example, notice that each step of the Sierpinski gasket iteration removes one quarter of the remaining area. If this process is continued indefinitely, we would end up essentially removing all the area, meaning we started with a 2-dimensional area, and somehow end up with something less than that, but seemingly more than just a 1-dimensional line.

To explore this idea, we need to discuss dimension. Something like a line is 1-dimensional; it only has length. Any curve is 1-dimensional. Things like boxes and circles are 2-dimensional, since they have length and width, describing an area. Objects like boxes and cylinders have length, width, and height, describing a volume, and are 3-dimensional.

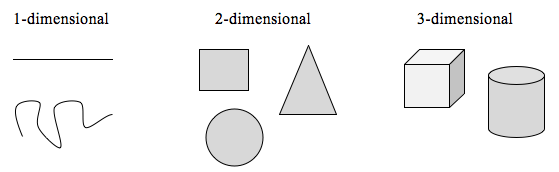
1-dimensional objects include a straight line and an irregular wavy line. 2-dimensional objects include a rectangle, a triangle, and a circle. 3-dimensional objects include a cube and a cylinder.

 

Certain rules apply for scaling objects, related to their dimension.

If I had a line with length 1, and wanted to scale its length by 2, I would need two copies of the original line. If I had a line of length 1, and wanted to scale its length by 3, I would need three copies of the original.

1, a horizontal line. 2, a horizontal line twice as long. 3, a horizontal line three times as long.

If I had a rectangle with length 2 and height 1, and wanted to scale its length and width by 2, I would need four copies of the original rectangle. If I wanted to scale the length and width by 3, I would need nine copies of the original rectangle.

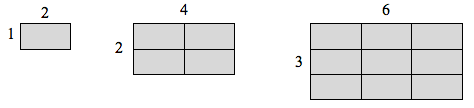
A rectangle with sides measuring 1 and 2. Next, four copies of that rectangle to form a larger rectangle with sides measuring 2 and 4. Next, nine copies of the first rectangle to form a larger rectangle with sides measuring 3 and 6.

If I had a cubical box with sides of length 1, and wanted to scale its length and width by 2, I would need eight copies of the original cube. If I wanted to scale the length and width by 3, I would need 27 copies of the original cube.

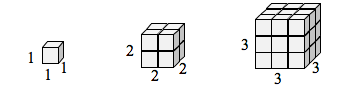
A cube with sides measuring 1 by 1 by 1. Next, eight copies of that cube to form a larger cube with sides measuring 2 by 2 by 2. Next, 27 copies of the original cube to form a larger cube measuring 3 by 3 by 3.

Notice that in the 1-dimensional case, copies needed = scale.

In the 2-dimensional case, copies needed = scale[latex]^{2}[/latex].

In the 3-dimensional case, copies needed = scale[latex]^{3}[/latex].

From these examples, we might infer a pattern.

Exponential notation

The relation below uses exponential notation. Recall that a number or a variable in a superscript position over a base number or variable is called an exponent. It indicates that the base should be used as a factor a number of times equal to the exponent.

Ex. [latex]2^{3}[/latex] indicates to use [latex]2[/latex] as a factor [latex]3[/latex] times.

[latex]2^{3}=2 \ast 2 \ast 2 = 8[/latex].

In the relation below, the equation [latex]C=S^{D}[/latex] indicates that the number of copies of the original shape [latex]C[/latex] can be found by multiplying a scaling factor [latex]S[/latex] by itself the same number of times as the dimension [latex]D[/latex].

Scaling-Dimension Relation

To scale a D-dimensional shape by a scaling factor S, the number of copies C of the original shape needed will be given by:

[latex]\text{Copies}=\text{Scale}^{\text{Dimension}}[/latex], or [latex]C=S^{D}[/latex]

a preview of the properties of equality

You may have encountered the properties of equality before. These properties essentially state that we are permitted to perform an identical operation on both sides of an equation without changing the equation’s value. This allows us to rearrange an equation until just the variable is on one side of an equal symbol and a number or value is on the other. When we do this we say we are solving the equation.

Ex. Say we are given the following statement of equality. What value of the variable [latex]x[/latex] will make the equation a true statement?

[latex]x+2=11[/latex]

This equation asks the question what number when increased by 2 is 11? Clearly [latex]9 + 2 = 11[/latex]. We could have solved this equation algebraically by subtracting 2 from both sides of the equation, leaving the [latex]x[/latex] isolate on one side.

[latex]x+2=11[/latex]

[latex]x+2-2 = 11-2[/latex]

[latex]x = 9[/latex].

You’ll learn later in the course that there are many operations you can perform to both sides of an equation in order to solve an equation. That is, to isolate a variable and reveal its solution.

The example below uses logarithms to solve for a variable contained in the exponent. You haven’t seen this technique before in this course, but it will come up for us later. In the meantime, you can use logarithms without understanding the underlying process by using a calculator by employing an alternative form of the scaling-dimension relation,

[latex]D=\frac{\log\left(C\right)}{\log(S)}[/latex].

 

Example

Use the scaling-dimension relation to determine the dimension of the Sierpinski gasket.

Suppose we define the original gasket to have side length 1. The larger gasket shown is twice as wide and twice as tall, so has been scaled by a factor of 2.

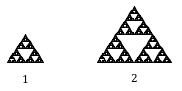
Sierpinski gasket triangle. Next, a bigger triangle made of three Sierpinski gasket triangles and a white triangle in the center.

Notice that to construct the larger gasket, 3 copies of the original gasket are needed.

Using the scaling-dimension relation [latex]C=S^{D}[/latex], we obtain the equation [latex]3=2^{D}[/latex].

Since [latex]2^{1}=2[/latex] and [latex]2^{2}=4[/latex], we can immediately see that D is somewhere between 1 and 2; the gasket is more than a 1-dimensional shape, but we’ve taken away so much area its now less than 2-dimensional.

Solving the equation [latex]3=2^{D}[/latex] requires logarithms. If you studied logarithms earlier, you may recall how to solve this equation (if not, just skip to the box below and use that formula with the log key on a calculator):

Take the logarithm of both sides.

[latex]3={{2}^{D}}[/latex]

Use the exponent property of logs.

[latex]\log(3)=\log\left({{2}^{D}}\right)[/latex]

Divide by log(2).

[latex]\log(3)=D\log\left(2\right)[/latex]

The dimension of the gasket is about 1.585.

[latex]D=\frac{\log\left(3\right)}{\log(2)}\approx1.585[/latex]

Scaling-Dimension Relation, to find Dimension

To find the dimension D of a fractal, determine the scaling factor S and the number of copies C of the original shape needed, then use the formula

[latex]D=\frac{\log\left(C\right)}{\log(S)}[/latex]

Try It

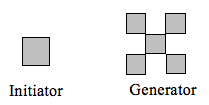
Determine the fractal dimension of the fractal produced using the initiator and generator.

Initiator is a square. Generator is five squares forming a checkered pattern.

In the following video, we present a worked example of how to determine the dimension of the Sierpinski gasket