Learning Outcomes
- Identify the carrying capacity in a logistic growth model
- Use a logistic growth model to predict growth
Limits on Exponential Growth
In our basic exponential growth scenario, we had a recursive equation of the form
[latex]P_{n}= P_{n-1} + r P_{n-1}[/latex]
In a confined environment, however, the growth rate may not remain constant. In a lake, for example, there is some maximum sustainable population of fish, also called a carrying capacity.
Carrying Capacity
The carrying capacity, or maximum sustainable population, is the largest population that an environment can support.
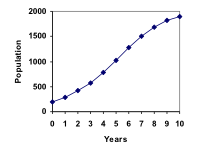
For our fish, the carrying capacity is the largest population that the resources in the lake can sustain. If the population in the lake is far below the carrying capacity, then we would expect the population to grow essentially exponentially. However, as the population approaches the carrying capacity, there will be a scarcity of food and space available, and the growth rate will decrease. If the population exceeds the carrying capacity, there won’t be enough resources to sustain all the fish and there will be a negative growth rate, causing the population to decrease back to the carrying capacity.
If the carrying capacity was [latex]5000[/latex], the growth rate might vary something like that in the graph shown.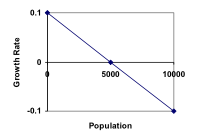
Recall the formula for slope
Slope, the measure of the steepness of a line, is given be the difference in the vertical distance over the distance in the horizontal distance between [latex]2[/latex] points. The line graphed above falls [latex]0.1[/latex] in growth rate for a corresponding increase in population of [latex]5000[/latex]. This gives the stated slope of
[latex]\dfrac{-0.1}{5000}[/latex], which we write conveniently as [latex]-\dfrac{0.1}{5000}[/latex].
This slope remains constant across the population change since, as the population increases another [latex]5000[/latex] to [latex]10,000[/latex], the growth rate falls again by [latex]0.1[/latex].
Note that this is a linear equation with intercept at [latex]0.1[/latex] and slope [latex]-\frac{0.1}{5000}[/latex], so we could write an equation for this adjusted growth rate as:
[latex]r_{adjusted} =[/latex] [latex]0.1-\frac{0.1}{5000}P=0.1\left(1-\frac{P}{5000}\right)[/latex]
Substituting this in to our original exponential growth model for [latex]r[/latex] gives
[latex]{{P}_{n}}={{P}_{n-1}}+0.1\left(1-\frac{{{P}_{n-1}}}{5000}\right){{P}_{n-1}}[/latex]
View the following for a detailed explanation of the concept.
how did they do that?
The video below provides a demonstration, but it may be helpful to recap the process in writing as well.
The recursive formula for exponential growth (listed again at the top of this page), [latex]P_n=P_{n-1}+rP_{n-1}[/latex], may be rewritten by factoring out the [latex]P_{n-1}[/latex] from both terms on the right hand side of the equation. This gives
[latex]P_n=P_{n-1}\left(1+r\right)[/latex]
[latex]P_n=\left(1+r\right)P_{n-1}[/latex], equivalently.
We can write an equation of the line formed in the graph above. It’s vertical intercept is [latex]0.1[/latex] and slope is [latex]\dfrac{-0.1}{5000}[/latex]. In the form of a linear equation, [latex]y=mx+b[/latex] with [latex]y=r[/latex] for growth rate and [latex]x=P[/latex] for population, this gives
[latex]r=-\dfrac{0.1}{5000}P+0.1[/latex]
[latex]r=0.1-\dfrac{0.1}{5000}P[/latex]
[latex]r=0.1\left(1-\dfrac{P}{5000}\right)[/latex] by factoring [latex]0.1[/latex] from both terms.
Now we can build the adjusted exponential growth model for this situation.
[latex]P_n=P_{n-1}+\left(r\right)P_{n-1}[/latex]
[latex]P_n=P_{n-1}+0.1\left(1-\dfrac{P_{n-1}}{5000}\right)P_{n-1}[/latex], substituting the equivalent value for r in our situation, and the initial population [latex]P_{n-1}[/latex] for [latex]P[/latex].
Putting this in general terms for any such situation, we can replace the particular growth rate with the variable [latex]r[/latex] and the maximal population of [latex]5000[/latex] in this case with a variable [latex]K[/latex] that represents carrying capacity. This gives us a general model for constrained growth called the logistic model.
[latex]P_n=P_{n-1}+r\left(1-\dfrac{P_{n-1}}{K}\right)P_{n-1}[/latex]
Logistic Growth
If a population is growing in a constrained environment with carrying capacity [latex]K[/latex], and absent constraint would grow exponentially with growth rate [latex]r[/latex], then the population behavior can be described by the logistic growth model:
[latex]{{P}_{n}}={{P}_{n-1}}+r\left(1-\frac{{{P}_{n-1}}}{K}\right){{P}_{n-1}}[/latex]
Unlike linear and exponential growth, logistic growth behaves differently if the populations grow steadily throughout the year or if they have one breeding time per year. The recursive formula provided above models generational growth, where there is one breeding time per year (or, at least a finite number); there is no explicit formula for this type of logistic growth.
Examples
A forest is currently home to a population of [latex]200[/latex] rabbits. The forest is estimated to be able to sustain a population of [latex]2000[/latex] rabbits. Absent any restrictions, the rabbits would grow by [latex]50\%[/latex] per year. Predict the future population using the logistic growth model.
View more about this example below.
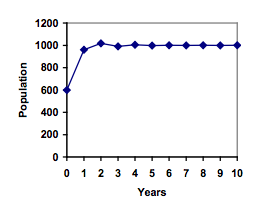
On an island that can support a population of [latex]1000[/latex] lizards, there is currently a population of [latex]600[/latex]. These lizards have a lot of offspring and not a lot of natural predators, so have very high growth rate, around [latex]150\%[/latex]. Calculating out the next couple generations:
[latex]{{P}_{1}}={{P}_{0}}+1.50\left(1-\frac{{{P}_{0}}}{1000}\right){{P}_{0}}=600+1.50\left(1-\frac{600}{1000}\right)600=960[/latex]
[latex]{{P}_{2}}={{P}_{1}}+1.50\left(1-\frac{{{P}_{1}}}{1000}\right){{P}_{1}}=960+1.50\left(1-\frac{960}{1000}\right)960=1018[/latex]
Interestingly, even though the factor that limits the growth rate slowed the growth a lot, the population still overshot the carrying capacity. We would expect the population to decline the next year.
[latex]{{P}_{3}}={{P}_{2}}+1.50\left(1-\frac{{{P}_{3}}}{1000}\right){{P}_{3}}=1018+1.50\left(1-\frac{1018}{1000}\right)1018=991[/latex]
Calculating out a few more years and plotting the results, we see the population wavers above and below the carrying capacity, but eventually settles down, leaving a steady population near the carrying capacity.
Try It
A field currently contains [latex]20[/latex] mint plants. Absent constraints, the number of plants would increase by [latex]70\%[/latex] each year, but the field can only support a maximum population of [latex]300[/latex] plants. Use the logistic model to predict the population in the next three years.
Example
On a neighboring island to the one from the previous example, there is another population of lizards, but the growth rate is even higher – about [latex]205\%[/latex].
Calculating out several generations and plotting the results, we get a surprise: the population seems to be oscillating between two values, a pattern called a 2-cycle.
While it would be tempting to treat this only as a strange side effect of mathematics, this has actually been observed in nature. Researchers from the University of California observed a stable 2-cycle in a lizard population in California.[1]
Taking this even further, we get more and more extreme behaviors as the growth rate increases higher. It is possible to get stable 4-cycles, 8-cycles, and higher. Quickly, though, the behavior approaches chaos (remember the movie Jurassic Park?).
All of the lizard island examples are discussed in this video.