Locating and Ordering Fractions and Mixed Numbers on the Number Line

Learning Outcomes

  • Locate and label improper and proper fractions on a number line
  • Order fractions and mixed numbers on a number line
  • Use inequality symbols to compare fractions and mixed numbers

Now we are ready to plot fractions on a number line. This will help us visualize fractions and understand their values.

Let us locate [latex]{\Large\frac{1}{5},\frac{4}{5}},3,3{\Large\frac{1}{3},\frac{7}{4},\frac{9}{2}},5[/latex], and [latex]{\Large\frac{8}{3}}[/latex] on the number line.

We will start with the whole numbers [latex]3[/latex] and [latex]5[/latex] because they are the easiest to plot.

A number line is shown with the numbers 3, 4, and 5. There are red dots at 3 and at 5.
The proper fractions listed are [latex]{\Large\frac{1}{5}}[/latex] and [latex]{\Large\frac{4}{5}}[/latex]. We know proper fractions have values less than one, so [latex]{\Large\frac{1}{5}}[/latex] and [latex]{\Large\frac{4}{5}}[/latex] are located between the whole numbers [latex]0[/latex] and [latex]1[/latex]. The denominators are both [latex]5[/latex], so we need to divide the segment of the number line between [latex]0[/latex] and [latex]1[/latex] into five equal parts. We can do this by drawing four equally spaced marks on the number line, which we can then label as [latex]{\Large\frac{1}{5},\frac{2}{5},\frac{3}{5}}[/latex], and [latex]{\Large\frac{4}{5}}[/latex].

Now plot points at [latex]{\Large\frac{1}{5}}[/latex] and [latex]{\Large\frac{4}{5}}[/latex].

A number line is shown. It shows 0, 1 fifth, 2 fifths, 3 fifths, 4 fifths, and 1. There are red dots at 1 fifth and at 4 fifths.
The only mixed number to plot is [latex]3{\Large\frac{1}{3}}[/latex]. Between what two whole numbers is [latex]3{\Large\frac{1}{3}}[/latex]? Remember that a mixed number is a whole number plus a proper fraction, so [latex]3{\Large\frac{1}{3}}>3[/latex]. Since it is greater than [latex]3[/latex], but not a whole unit greater, [latex]3{\Large\frac{1}{3}}[/latex] is between [latex]3[/latex] and [latex]4[/latex]. We need to divide the portion of the number line between [latex]3[/latex] and [latex]4[/latex] into three equal pieces (thirds) and plot [latex]3{\Large\frac{1}{3}}[/latex] at the first mark.

A number line is shown with whole number 0 through 5. Between 3 and 4, 3 and 1 third and 3 and 2 thirds are labeled. There is a red dot at 3 and 1 third.
Finally, look at the improper fractions [latex]{\Large\frac{7}{4},\frac{9}{2}}[/latex], and [latex]{\Large\frac{8}{3}}[/latex]. Locating these points will be easier if you change each of them to a mixed number.

[latex]{\Large\frac{7}{4}}=1{\Large\frac{3}{4}},{\Large\frac{9}{2}}=4{\Large\frac{1}{2}},{\Large\frac{8}{3}}=2{\Large\frac{2}{3}}[/latex]

Here is the number line with all the points plotted.

A number line is shown with whole numbers 0 through 6. Between 0 and 1, 1 fifth and 4 fifths are labeled and shown with red dots. Between 1 and 2, 7 fourths is labeled and shown with a red dot. Between 2 and 3, 8 thirds is labeled and shown with a red dot. Between 3 and 4, 3 and 1 third is labeled and shown with a red dot. Between 4 and 5, 9 halves is labeled and shown with a red dot.

Example

Locate and label the following on a number line: [latex]{\Large\frac{3}{4},\frac{4}{3},\frac{5}{3}},4{\Large\frac{1}{5}}[/latex], and [latex]{\Large\frac{7}{2}}[/latex].

Solution:
Start by locating the proper fraction [latex]{\Large\frac{3}{4}}[/latex]. It is between [latex]0[/latex] and [latex]1[/latex]. To do this, divide the distance between [latex]0[/latex] and [latex]1[/latex] into four equal parts. Then plot [latex]{\Large\frac{3}{4}}[/latex].

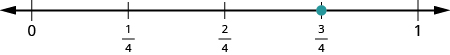
A number line is shown. It shows 0, 1 fourth, 2 fourths, 3 fourths, and 1. There is a red dot at 3 fourths.
Next, locate the mixed number [latex]4{\Large\frac{1}{5}}[/latex]. It is between [latex]4[/latex] and [latex]5[/latex] on the number line. Divide the number line between [latex]4[/latex] and [latex]5[/latex] into five equal parts, and then plot [latex]4{\Large\frac{1}{5}}[/latex] one-fifth of the way between [latex]4[/latex] and [latex]5[/latex] .

A number line is shown. It shows 4, 4 and 1 fifth, 4 and 2 fifths, 4 and 3 fifths, 4 and 4 fifths, and 5. There is a red dot at 4 and 1 fifth.
Now locate the improper fractions [latex]{\Large\frac{4}{3}}[/latex] and [latex]{\Large\frac{5}{3}}[/latex]. It is easier to plot them if we convert them to mixed numbers first.

[latex]{\Large\frac{4}{3}}=1{\Large\frac{1}{3}},{\Large\frac{5}{3}}=1{\Large\frac{2}{3}}[/latex]
Divide the distance between [latex]1[/latex] and [latex]2[/latex] into thirds.

A number line is shown. It shows 1, 1 and 1 third, 1 and 2 thirds, and 2. Below 1 it says 3 thirds. Below 1 and 1 third it says 4 thirds. Below 1 and 2 thirds it says 5 thirds. Below 2 it says 6 thirds. There are red dots at 1 and 1 third and 1 and 2 thirds.
Next let us plot [latex]{\Large\frac{7}{2}}[/latex]. We write it as a mixed number, [latex]{\Large\frac{7}{2}}=3{\Large\frac{1}{2}}[/latex] . Plot it between [latex]3[/latex] and [latex]4[/latex].

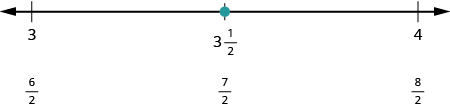
A number line is shown. It shows 3, 3 and 1 half, and 4. Below 3 it says 6 halves. Below 3 and 1 half it says 7 halves. Below 4 it says 8 halves. There is a red dot at 3 and 1 half.
The number line shows all the numbers located on the number line.

A number line is shown. It shows the whole numbers 0 through 5. Between any 2 numbers are 10 tick marks. Between 0 and 1, between the 7th and 8th tick mark, 3 fourths is labeled and shown with a red dot. Between 1 and 2, 4 thirds and 5 thirds are labeled and shown with red dots. Between 3 and 4, 7 halves is labeled and shown with a red dot. Between 4 and 5, 4 and 1 fifth is labeled and shown with a red dot.

 

try it

Watch the following video to see more examples of how to locate fractions on a number line.

In Introduction to Integers, we defined the opposite of a number. It is the number that is the same distance from zero on the number line but on the opposite side of zero. We saw, for example, that the opposite of [latex]7[/latex] is [latex]-7[/latex] and the opposite of [latex]-7[/latex] is [latex]7[/latex].

A number line is shown. It shows the numbers negative 7, 0 and 7. There are red dots at negative 7 and 7. The space between negative 7 and 0 is labeled as 7 units. The space between 0 and 7 is labeled as 7 units.
Fractions have opposites, too. The opposite of [latex]{\Large\frac{3}{4}}[/latex] is [latex]-{\Large\frac{3}{4}}[/latex]. It is the same distance from [latex]0[/latex] on the number line, but on the opposite side of [latex]0[/latex].

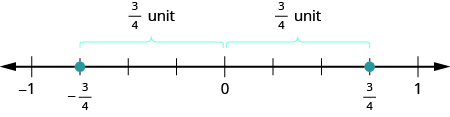
A number line is shown. It shows the numbers negative 1, negative 3 fourths, 0, 3 fourths, and 1. There are red dots at negative 3 fourths and 3 fourths. The space between negative 3 fourths and 0 is labeled as 3 fourths of a unit. The space between 0 and 3 fourths is labeled as 3 fourths of a unit.
Thinking of negative fractions as the opposite of positive fractions will help us locate them on the number line. To locate [latex]-{\Large\frac{15}{8}}[/latex] on the number line, first think of where [latex]{\Large\frac{15}{8}}[/latex] is located. It is an improper fraction, so we first convert it to the mixed number [latex]1{\Large\frac{7}{8}}[/latex] and see that it will be between [latex]1[/latex] and [latex]2[/latex] on the number line. So its opposite, [latex]-{\Large\frac{15}{8}}[/latex], will be between [latex]-1[/latex] and [latex]-2[/latex] on the number line.

A number line is shown. It shows the numbers negative 2, negative 1, 0, 1, and 2. Between negative 2 and negative 1, negative 1 and 7 eighths is labeled and marked with a red dot. The distance between negative 1 and 7 eighths and 0 is marked as 15 eighths units. Between 1 and 2, 1 and 7 eighths is labeled and marked with a red dot. The distance between 0 and 1 and 7 eighths is marked as 15 eighths units.

Example

Locate and label the following on the number line: [latex]{\Large\frac{1}{4}},-{\Large\frac{1}{4}},1{\Large\frac{1}{3}},-1{\Large\frac{1}{3}},{\Large\frac{5}{2}}[/latex], and [latex]-{\Large\frac{5}{2}}[/latex].

 

Try it

In the next video we give more examples of how to locate negative and positive fractions on a number line.

Order Fractions and Mixed Numbers

We can use the inequality symbols to order fractions. Remember that [latex]a>b[/latex] means that [latex]a[/latex] is to the right of [latex]b[/latex] on the number line. As we move from left to right on a number line, the values increase.

Example

Order each of the following pairs of numbers, using [latex]<[/latex]; or [latex]>:[/latex]

  1. [latex]-{\Large\frac{2}{3}}[/latex] ____ [latex]- 1[/latex]
  2. [latex]-3{\Large\frac{1}{2}}[/latex] ____ [latex]- 3[/latex]
  3. [latex]-{\Large\frac{3}{7}}[/latex] ____ [latex]{\Large\frac{3}{8}}[/latex]
  4. [latex]-2[/latex] ____ [latex]{\Large\frac{-16}{9}}[/latex]

 

Try it

In the following video we show another example of how to order integers, fractions and mixed numbers using inequality symbols.