Problem Set: Fractions

Representing parts of a whole

Using Models to Represent Fractions

In the following exercises, name the fraction of each figure that is shaded.

Exercise 1

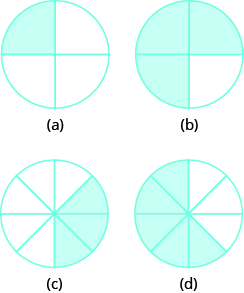
In part

Exercise 2

In part

Using Models to Represent Fractions

In the following exercises, shade parts of circles or squares to model the following fractions.

  1. [latex]\Large\frac{1}{2}[/latex]

  2. [latex]\Large\frac{1}{3}[/latex]
  3. [latex]\Large\frac{3}{4}[/latex]

  4. [latex]\Large\frac{2}{5}[/latex]
  5. [latex]\Large\frac{5}{6}[/latex]

  6. [latex]\Large\frac{7}{8}[/latex]
  7. [latex]\Large\frac{5}{8}[/latex]

  8. [latex]\Large\frac{7}{10}[/latex]

Using Models to Represent Mixed Numbers

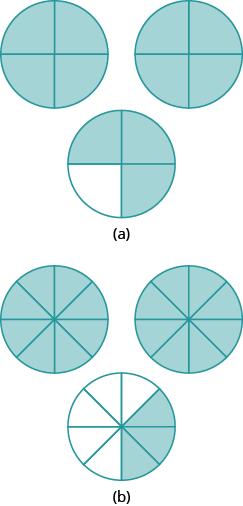
In the following exercises, use fraction circles to make wholes, if possible, with the following pieces.

  1. [latex]3[/latex] thirds

  2. [latex]8[/latex] eighths
  3. [latex]7[/latex] sixths

  4. [latex]4[/latex] thirds
  5. [latex]7[/latex] fifths

  6. [latex]7[/latex] fourths

Using Models to Represent Mixed Numbers

In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.

Exercise 1

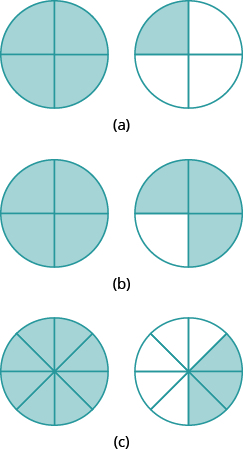
In part

Exercise 2

In part

Exercise 3

In part

Using Models to Represent Mixed Numbers

In the following exercises, draw fraction circles to model the given fraction.

  1. [latex]\Large\frac{3}{3}[/latex]
  2. [latex]\Large\frac{4}{4}[/latex]

  3. [latex]\Large\frac{7}{4}[/latex]
  4. [latex]\Large\frac{5}{3}[/latex]

  5. [latex]\Large\frac{11}{6}[/latex]
  6. [latex]\Large\frac{13}{8}[/latex]

  7. [latex]\Large\frac{10}{3}[/latex]
  8. [latex]\Large\frac{9}{4}[/latex]

Converting Between Improper Fractions and Mixed Numbers

Write an Improper Fraction as a Mixed Number

In the following exercises, rewrite the improper fraction as a mixed number.

  1. [latex]\Large\frac{3}{2}[/latex]
  2. [latex]\Large\frac{5}{3}[/latex]

  3. [latex]\Large\frac{11}{4}[/latex]
  4. [latex]\Large\frac{13}{5}[/latex]

  5. [latex]\Large\frac{25}{6}[/latex]
  6. [latex]\Large\frac{28}{9}[/latex]

  7. [latex]\Large\frac{42}{13}[/latex]
  8. [latex]\Large\frac{47}{15}[/latex]

Write a Mixed Number as an Improper Fraction

In the following exercises, rewrite the mixed number as an improper fraction.

  1. [latex]1\Large\frac{2}{3}[/latex]
  2. [latex]1\Large\frac{2}{5}[/latex]

  3. [latex]2\Large\frac{1}{4}[/latex]
  4. [latex]2\Large\frac{5}{6}[/latex]

  5. [latex]2\Large\frac{7}{9}[/latex]
  6. [latex]2\Large\frac{5}{7}[/latex]

  7. [latex]3\Large\frac{4}{7}[/latex]
  8. [latex]3\Large\frac{5}{9}[/latex]

Modeling and Finding Equivalent Fractions

Modeling Equivalent Fractions

In the following exercises, use fraction tiles or draw a figure to find equivalent fractions.

  1. How many sixths equal one-third?
  2. How many twelfths equal one-third?

  3. How many eighths equal three-fourths?
  4. How many twelfths equal three-fourths?

  5. How many fourths equal three-halves?
  6. How many sixths equal three-halves?

Finding Equivalent Fractions

In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.

  1. [latex]\Large\frac{1}{4}[/latex]
  2. [latex]\Large\frac{1}{3}[/latex]

  3. [latex]\Large\frac{3}{8}[/latex]
  4. [latex]\Large\frac{5}{6}[/latex]

  5. [latex]\Large\frac{2}{7}[/latex]
  6. [latex]\Large\frac{5}{9}[/latex]

Locating and Ordering Fractions and Mixed Numbers on the Number Line

Locating Fractions on the Number Line

In the following exercises, plot the numbers on a number line.

  1. [latex]\Large\frac{2}{3},\Large\frac{5}{4},\Large\frac{12}{5}[/latex]
  2. [latex]\Large\frac{1}{3},\Large\frac{7}{4},\Large\frac{13}{5}[/latex]

  3. [latex]\Large\frac{1}{4},\Large\frac{9}{5},\Large\frac{11}{3}[/latex]
  4. [latex]\Large\frac{7}{10},\Large\frac{5}{2},\Large\frac{13}{8},\normalsize 3[/latex]

  5. [latex]2\Large\frac{1}{3}\normalsize ,-2\Large\frac{1}{3}[/latex]
  6. [latex]1\Large\frac{3}{4}\normalsize ,-1\Large\frac{3}{5}[/latex]

  7. [latex]\Large\frac{3}{4},-\Large\frac{3}{4}\normalsize ,1\Large\frac{2}{3}\normalsize ,-1\Large\frac{2}{3},\Large\frac{5}{2},-\Large\frac{5}{2}[/latex]
  8. [latex]\Large\frac{2}{5},-\Large\frac{2}{5}\normalsize ,1\Large\frac{3}{4}\normalsize ,-1\Large\frac{3}{4},\Large\frac{8}{3},-\Large\frac{8}{3}[/latex]

Ordering Fractions on the Number Line

In the following exercises, order each of the following pairs of numbers, using [latex]<[/latex] or [latex]>[/latex].

  1. [latex]-1\text{ __}-\Large\frac{1}{4}[/latex]
  2. [latex]-1\text{ __}-\Large\frac{1}{3}[/latex]

  3. [latex]-2\Large\frac{1}{2}\normalsize\text{ __}-3[/latex]
  4. [latex]-1\Large\frac{3}{4}\normalsize\text{ __}-2[/latex]

  5. [latex]-\Large\frac{5}{12}\text{ __}-\Large\frac{7}{12}[/latex]
  6. [latex]-\Large\frac{9}{10}\text{ __}-\Large\frac{3}{10}[/latex]

  7. [latex]-3\text{ __}-\Large\frac{13}{5}[/latex]
  8. [latex]-4\text{ __}-\Large\frac{23}{6}[/latex]

Everyday Math

Music Measures

A choreographed dance is broken into counts. A [latex]\Large\frac{1}{1}[/latex] count has one step in a count, a [latex]\Large\frac{1}{2}[/latex] count has two steps in a count and a [latex]\Large\frac{1}{3}[/latex] count has three steps in a count. How many steps would be in a [latex]\Large\frac{1}{5}[/latex] count? What type of count has four steps in it?

Music Measures

Fractions are used often in music. In [latex]\Large\frac{4}{4}[/latex] time, there are four quarter notes in one measure.

  1. How many measures would eight quarter notes make?

  2. The song “Happy Birthday to You” has [latex]25[/latex] quarter notes. How many measures are there in “Happy Birthday to You?”

Baking

Nina is making five pans of fudge to serve after a music recital. For each pan, she needs [latex]\Large\frac{1}{2}[/latex] cup of walnuts.

  1. How many cups of walnuts does she need for five pans of fudge?
  2. Do you think it is easier to measure this amount when you use an improper fraction or a mixed number? Why?

Writing Exercises

Give an example from your life experience (outside of school) where it was important to understand fractions.

Explain how you locate the improper fraction [latex]\Large\frac{21}{4}[/latex] on a number line on which only the whole numbers from [latex]0[/latex] through [latex]10[/latex] are marked.

Multiplying and Dividing Fractions

Simplify Fractions

In the following exercises, simplify each fraction. Do not convert any improper fractions to mixed numbers.

  1. [latex]\Large\frac{7}{21}[/latex]

  2. [latex]\Large\frac{8}{24}[/latex]
  3. [latex]\Large\frac{15}{20}[/latex]

  4. [latex]\Large\frac{12}{18}[/latex]
  5. [latex]-\Large\frac{40}{88}[/latex]

  6. [latex]-\Large\frac{63}{99}[/latex]
  7. [latex]-\Large\frac{108}{63}[/latex]

  8. [latex]-\Large\frac{104}{48}[/latex]
  9. [latex]\Large\frac{120}{252}[/latex]

  10. [latex]\Large\frac{182}{294}[/latex]
  11. [latex]-\Large\frac{168}{192}[/latex]

  12. [latex]-\Large\frac{140}{224}[/latex]
  13. [latex]\Large\frac{11x}{11y}[/latex]

  14. [latex]\Large\frac{15a}{15b}[/latex]
  15. [latex]-\Large\frac{3x}{12y}[/latex]

  16. [latex]-\Large\frac{4x}{32y}[/latex]
  17. [latex]\Large\frac{14{x}^{2}}{21y}[/latex]

  18. [latex]\Large\frac{24a}{32{b}^{2}}[/latex]

Multiply Fractions

In the following exercises, use a diagram to model.

  1. [latex]\Large\frac{1}{2}\cdot\Large\frac{2}{3}[/latex]
  2. [latex]\Large\frac{1}{3}[/latex]
  3. [latex]\Large\frac{1}{2}\cdot\Large\frac{5}{8}[/latex]
  4. [latex]\Large\frac{1}{3}\cdot\Large\frac{5}{6}[/latex]
  5. [latex]\Large\frac{5}{18}[/latex]
  6. [latex]\Large\frac{1}{3}\cdot\Large\frac{2}{5}[/latex]

Multiply and Simplify Fractions

In the following exercises, multiply, and write the answer in simplified form.

  1. [latex]\Large\frac{2}{5}\cdot\Large\frac{1}{3}[/latex]

  2. [latex]\Large\frac{1}{2}\cdot\Large\frac{3}{8}[/latex]
  3. [latex]\Large\frac{3}{4}\cdot\Large\frac{9}{10}[/latex]

  4. [latex]\Large\frac{4}{5}\cdot\Large\frac{2}{7}[/latex]
  5. [latex]-\Large\frac{2}{3}\left(-\Large\frac{3}{8}\right)[/latex]

  6. [latex]-\Large\frac{3}{4}\left(-\Large\frac{4}{9}\right)[/latex]
  7. [latex]-\Large\frac{5}{9}\cdot\Large\frac{3}{10}[/latex]

  8. [latex]-\Large\frac{3}{8}\cdot\Large\frac{4}{15}[/latex]
  9. [latex]\Large\frac{7}{12}\left(-\Large\frac{8}{21}\right)[/latex]

  10. [latex]\Large\frac{5}{12}\left(-\Large\frac{8}{15}\right)[/latex][latex]\left(-\Large\frac{14}{15}\right)\left(\Large\frac{9}{20}\right)[/latex]

  11. [latex]\left(-\Large\frac{9}{10}\right)\left(\Large\frac{25}{33}\right)[/latex]
  12. [latex]\left(-\Large\frac{63}{84}\right)\left(-\Large\frac{44}{90}\right)[/latex]

  13. [latex]\left(-\Large\frac{33}{60}\right)\left(-\Large\frac{40}{88}\right)[/latex]
  14. [latex]4\cdot\Large\frac{5}{11}[/latex]
  15. [latex]\Large\frac{20}{11}[/latex]
  16. [latex]5\cdot\Large\frac{8}{3}[/latex]
  17. [latex]\Large\frac{3}{7}\normalsize\cdot 21n[/latex]

  18. [latex]\Large\frac{5}{6}\normalsize\cdot 30m[/latex]
  19. [latex]-28p\left(-\Large\frac{1}{4}\right)[/latex]

  20. [latex]-51q\left(-\Large\frac{1}{3}\right)[/latex]
  21. [latex]-8\Large\left(\frac{17}{4}\right)[/latex]

  22. [latex]\Large\frac{14}{5}\normalsize\left(-15\right)[/latex]
  23. [latex]-1\Large\left(-\frac{3}{8}\right)[/latex]
  24. [latex]\Large\frac{3}{8}[/latex]
  25. [latex]\left(-1\right)\Large\left(-\frac{6}{7}\right)[/latex]
  26. [latex]{\Large\left(\frac{2}{3}\right)}^{3}[/latex]
  27. [latex]\Large\frac{8}{27}[/latex]
  28. [latex]{\Large\left(\frac{4}{5}\right)}^{2}[/latex]
  29. [latex]{\Large\left(\frac{6}{5}\right)}^{4}[/latex]
  30. [latex]\Large\frac{1296}{625}[/latex]
  31. [latex]{\Large\left(\frac{4}{7}\right)}^{4}[/latex]

Find Reciprocals

In the following exercises, find the reciprocal.

  1. [latex]\Large\frac{3}{4}[/latex]

  2. [latex]\Large\frac{2}{3}[/latex]
  3. [latex]-\Large\frac{5}{17}[/latex]

  4. [latex]-\Large\frac{6}{19}[/latex]
  5. [latex]\Large\frac{11}{8}[/latex]

  6. [latex]-13[/latex]
  7. [latex]-19[/latex]

  8. [latex]-1[/latex]

Find Reciprocals

Exercise 1

Fill in the chart.

Opposite Absolute Value Reciprocal
[latex]-\Large\frac{7}{11}[/latex]
[latex]\Large\frac{4}{5}[/latex]
[latex]\Large\frac{10}{7}[/latex]
[latex]-\large 8[/latex]

Exercise 2

Fill in the chart.

Opposite Absolute Value Reciprocal
[latex]-\Large\frac{3}{13}[/latex]
[latex]\Large\frac{9}{14}[/latex]
[latex]\Large\frac{15}{7}[/latex]
[latex]-\large 9[/latex]

Divide Fractions

In the following exercises, model each fraction division.

  1. [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{4}[/latex]
  2. [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{8}[/latex]

  3. [latex]2\div\Large\frac{1}{5}[/latex]
  4. [latex]3\div\Large\frac{1}{4}[/latex]

Divide and Simplify Fractions

In the following exercises, divide, and write the answer in simplified form.

  1. [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{4}[/latex]
  2. [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{8}[/latex]

  3. [latex]\Large\frac{3}{4}\normalsize\div\Large\frac{2}{3}[/latex]
  4. [latex]\Large\frac{4}{5}\normalsize\div\Large\frac{3}{4}[/latex]
  5. [latex]\Large\frac{16}{15}[/latex]
  6. [latex]-\Large\frac{4}{5}\normalsize\div\Large\frac{4}{7}[/latex]
  7. [latex]-\Large\frac{3}{4}\normalsize\div\Large\frac{3}{5}[/latex]
  8. [latex]-\Large\frac{5}{4}[/latex]
  9. [latex]-\Large\frac{7}{9}\normalsize\div\Large\left(-\frac{7}{9}\right)[/latex]
  10. [latex]-\Large\frac{5}{6}\normalsize\div\Large\left(-\frac{5}{6}\right)[/latex]

  11. [latex]\Large\frac{3}{4}\normalsize\div\Large\frac{x}{11}[/latex]
  12. [latex]\Large\frac{2}{5}\normalsize\div\Large\frac{y}{9}[/latex]
  13. [latex]\Large\frac{18}{5y}[/latex]
  14. [latex]\Large\frac{5}{8}\normalsize\div\Large\frac{a}{10}[/latex]
  15. [latex]\Large\frac{5}{6}\normalsize\div\Large\frac{c}{15}[/latex]
  16. [latex]\Large\frac{25}{2c}[/latex]
  17. [latex]\Large\frac{5}{18}\normalsize\div\Large\left(-\frac{15}{24}\right)[/latex]
  18. [latex]\Large\frac{7}{18}\normalsize\div\Large\left(-\frac{14}{27}\right)[/latex]
  19. [latex]-\Large\frac{3}{4}[/latex]
  20. [latex]\Large\frac{7p}{12}\normalsize\div\Large\frac{21p}{8}[/latex]
  21. [latex]\Large\frac{5q}{12}\normalsize\div\Large\frac{15q}{8}[/latex]
  22. [latex]\Large\frac{2}{9}[/latex]
  23. [latex]\Large\frac{8u}{15}\normalsize\div\Large\frac{12v}{25}[/latex]
  24. [latex]\Large\frac{12r}{25}\normalsize\div\Large\frac{18s}{35}[/latex]
  25. [latex]\Large\frac{14r}{15s}[/latex]
  26. [latex]-5\normalsize\div\Large\frac{1}{2}[/latex]
  27. [latex]-3\normalsize\div\Large\frac{1}{4}[/latex]

  28. [latex]\Large\frac{3}{4}\normalsize\div\left(-12\right)[/latex]
  29. [latex]\Large\frac{2}{5}\normalsize\div\left(-10\right)[/latex]
  30. [latex]-\Large\frac{1}{25}[/latex]
  31. [latex]-18\normalsize\div\Large\left(-\frac{9}{2}\right)[/latex]
  32. [latex]-15\normalsize\div\Large\left(-\frac{5}{3}\right)[/latex]

  33. [latex]\Large\frac{1}{2}\normalsize\div\Large\left(-\frac{3}{4}\right)\normalsize\div\Large\frac{7}{8}[/latex]
  34. [latex]\Large\frac{11}{2}\normalsize\div\Large\frac{7}{8}\normalsize\cdot\Large\frac{2}{11}[/latex]
  35. [latex]\Large\frac{8}{7}[/latex]

Everyday Math

Baking

  1. A recipe for chocolate chip cookies calls for [latex]\Large\frac{3}{4}[/latex] cup brown sugar. Imelda wants to double the recipe.
    How much brown sugar will Imelda need? Show your calculation. Write your result as an improper fraction and as a mixed number.
  2. Measuring cups usually come in sets of [latex]\Large\frac{1}{8},\Large\frac{1}{4},\Large\frac{1}{3},\Large\frac{1}{2}\normalsize ,\text{ and }1[/latex] cup. Draw a diagram to show two different ways that Imelda could measure the brown sugar needed to double the recipe.

Baking

Nina is making [latex]4[/latex] pans of fudge to serve after a music recital. For each pan, she needs [latex]\Large\frac{2}{3}[/latex] cup of condensed milk.

  1. How much condensed milk will Nina need? Show your calculation. Write your result as an improper fraction and as a mixed number.

  2. Measuring cups usually come in sets of [latex]\Large\frac{1}{8},\Large\frac{1}{4},\Large\frac{1}{3},\Large\frac{1}{2}\normalsize ,\text{ and }1[/latex] cup. Draw a diagram to show two different ways that Nina could measure the condensed milk she needs.

Portions

Don purchased a bulk package of candy that weighs [latex]5[/latex] pounds. He wants to sell the candy in little bags that hold [latex]\Large\frac{1}{4}[/latex] pound. How many little bags of candy can he fill from the bulk package?

Portions

Kristen has [latex]\Large\frac{3}{4}[/latex] yards of ribbon. She wants to cut it into equal parts to make hair ribbons for her daughter’s [latex]6[/latex] dolls. How long will each doll’s hair ribbon be?

Writing Exercises

Explain how you find the reciprocal of a fraction.

Explain how you find the reciprocal of a negative fraction.

Rafael wanted to order half a medium pizza at a restaurant. The waiter told him that a medium pizza could be cut into [latex]6[/latex] or [latex]8[/latex] slices. Would he prefer [latex]3[/latex] out of [latex]6[/latex] slices or [latex]4[/latex] out of [latex]8[/latex] slices? Rafael replied that since he wasn’t very hungry, he would prefer [latex]3[/latex] out of [latex]6[/latex] slices. Explain what is wrong with Rafael’s reasoning.

Give an example from everyday life that demonstrates how [latex]\Large\frac{1}{2}\normalsize\cdot\Large\frac{2}{3}\normalsize\text{ is }\Large\frac{1}{3}[/latex].

Multiplying and Dividing Mixed Numbers and Complex Fractions

Multiply Mixed Numbers

In the following exercises, multiply and write the answer in simplified form.

  1. [latex]4\Large\frac{3}{8}\normalsize\cdot\Large\frac{7}{10}[/latex]
  2. [latex]2\Large\frac{4}{9}\normalsize\cdot\Large\frac{6}{7}[/latex]

  3. [latex]\Large\frac{15}{22}\normalsize\cdot 3\Large\frac{3}{5}[/latex]
  4. [latex]\Large\frac{25}{36}\normalsize\cdot 6\Large\frac{3}{10}[/latex]

  5. [latex]4\Large\frac{2}{3}\left(\normalsize -1\Large\frac{1}{8}\right)[/latex]
  6. [latex]2\Large\frac{2}{5}\left(\normalsize -2\Large\frac{2}{9}\right)[/latex]

  7. [latex]-4\Large\frac{4}{9}\normalsize\cdot 5\Large\frac{13}{16}[/latex]
  8. [latex]-1\Large\frac{7}{20}\normalsize\cdot 2\Large\frac{11}{12}[/latex]

Divide Mixed Numbers

In the following exercises, divide, and write your answer in simplified form.

  1. [latex]5\Large\frac{1}{3}\normalsize\div 4[/latex]
  2. [latex]13\Large\frac{1}{2}\normalsize\div 9[/latex]

  3. [latex]-12\Large\normalsize\div 3\Large\frac{3}{11}[/latex]
  4. [latex]-7\div 5\Large\frac{1}{4}[/latex]

  5. [latex]6\Large\frac{3}{8}\normalsize\div 2\Large\frac{1}{8}[/latex]
  6. [latex]2\Large\frac{1}{5}\normalsize\div 1\Large\frac{1}{10}[/latex]

  7. [latex]-9\Large\frac{3}{5}\normalsize\div\Large\left(\normalsize -1\Large\frac{3}{5}\right)[/latex]
  8. [latex]-18\Large\frac{3}{4}\normalsize\div\Large\left(\normalsize -3\Large\frac{3}{4}\right)[/latex]

Translate Phrases to Expressions with Fractions

In the following exercises, translate each English phrase into an algebraic expression.

  1. the quotient of [latex]5u[/latex] and [latex]11[/latex]
  2. the quotient of [latex]7v[/latex] and [latex]13[/latex]

  3. the quotient of [latex]p[/latex] and [latex]q[/latex]
  4. the quotient of [latex]a[/latex] and [latex]b[/latex]

  5. the quotient of [latex]r[/latex] and the sum of [latex]s[/latex] and [latex]10[/latex]
  6. the quotient of [latex]A[/latex] and the difference of [latex]3[/latex] and [latex]B[/latex]

Simplify Complex Fractions

In the following exercises, simplify the complex fraction.

  1. [latex]\displaystyle\Large\frac{\Large\frac{2}{3}}{\Large\frac{8}{9}}[/latex]
  2. [latex]\displaystyle\Large\frac{\Large\frac{4}{5}}{\Large\frac{8}{15}}[/latex]

  3. [latex]\displaystyle\Large\frac{-\Large\frac{8}{21}}{\Large\frac{12}{35}}[/latex]
  4. [latex]\displaystyle\Large\frac{-\Large\frac{9}{16}}{\Large\frac{33}{40}}[/latex]

  5. [latex]\displaystyle\frac{-\Large\frac{4}{5}}{2}[/latex]
  6. [latex]\displaystyle\frac{-\Large\frac{9}{10}}{3}[/latex]

  7. [latex]\displaystyle\frac{\Large\frac{2}{5}}{8}[/latex]
  8. [latex]\displaystyle\frac{\Large\frac{5}{3}}{10}[/latex]

  9. [latex]\displaystyle\Large\frac{\Large\frac{m}{3}}{\Large\frac{n}{2}}[/latex]
  10. [latex]\displaystyle\Large\frac{\Large\frac{r}{5}}{\Large\frac{s}{3}}[/latex]

  11. [latex]\displaystyle\Large\frac{-\Large\frac{x}{6}}{-\Large\frac{8}{9}}[/latex]
  12. [latex]\displaystyle\Large\frac{-\Large\frac{3}{8}}{-\Large\frac{y}{12}}[/latex]

  13. [latex]\displaystyle\frac{2\Large\frac{4}{5}}{\Large\frac{1}{10}}[/latex]
  14. [latex]\displaystyle\frac{4\Large\frac{2}{3}}{\Large\frac{1}{6}}[/latex]

  15. [latex]\displaystyle\Large\frac{\Large\frac{7}{9}}{\normalsize -2\Large\frac{4}{5}}[/latex]
  16. [latex]\displaystyle\Large\frac{\Large\frac{3}{8}}{\normalsize -6\Large\frac{3}{4}}[/latex]

Simplify Expressions with a Fraction Bar

In the following exercises, identify the equivalent fractions.

  1. Which of the following fractions are equivalent to [latex]\Large\frac{5}{-11}?[/latex]
    [latex]\Large\frac{-5}{-11},\Large\frac{-5}{11},\Large\frac{5}{11},-\Large\frac{5}{11}[/latex]
  2. Which of the following fractions are equivalent to [latex]\Large\frac{-4}{9}?[/latex]
    [latex]\Large\frac{-4}{-9},\Large\frac{-4}{9},\Large\frac{4}{9},-\Large\frac{4}{9}[/latex]

  3. Which of the following fractions are equivalent to [latex]-\Large\frac{11}{3}?[/latex]
    [latex]\Large\frac{-11}{3},\Large\frac{11}{3},\Large\frac{-11}{-3},\text{}\Large\frac{11}{-3}[/latex]
  4. Which of the following fractions are equivalent to [latex]-\Large\frac{13}{6}?[/latex]
    [latex]\Large\frac{13}{6},\Large\frac{13}{-6},\Large\frac{-13}{-6},\Large\frac{-13}{6}[/latex]

Simplify Fractions

In the following exercises, simplify.

  1. [latex]\Large\frac{4+11}{8}[/latex]
  2. [latex]\Large\frac{9+3}{7}[/latex]

  3. [latex]\Large\frac{22+3}{10}[/latex]
  4. [latex]\Large\frac{19 - 4}{6}[/latex]

  5. [latex]\Large\frac{48}{24 - 15}[/latex]
  6. [latex]\Large\frac{46}{4+4}[/latex]

  7. [latex]\Large\frac{-6+6}{8+4}[/latex]
  8. [latex]\Large\frac{-6+3}{17 - 8}[/latex]

  9. [latex]\Large\frac{22 - 14}{19 - 13}[/latex]
  10. [latex]\Large\frac{15+9}{18+12}[/latex]

  11. [latex]\Large\frac{5\cdot 8}{-10}[/latex]
  12. [latex]\Large\frac{3\cdot 4}{-24}[/latex]

  13. [latex]\Large\frac{4\cdot 3}{6\cdot 6}[/latex]
  14. [latex]\Large\frac{6\cdot 6}{9\cdot 2}[/latex]

  15. [latex]\Large\frac{{4}^{2}-1}{25}[/latex]
  16. [latex]\Large\frac{{7}^{2}+1}{60}[/latex]

  17. [latex]\Large\frac{8\cdot 3+2\cdot 9}{14+3}[/latex]
  18. [latex]\Large\frac{9\cdot 6 - 4\cdot 7}{22+3}[/latex]

  19. [latex]\Large\frac{15\cdot 5-{5}^{2}}{2\cdot 10}[/latex]
  20. [latex]\Large\frac{12\cdot 9-{3}^{2}}{3\cdot 18}[/latex]

  21. [latex]\Large\frac{5\cdot 6 - 3\cdot 4}{4\cdot 5 - 2\cdot 3}[/latex]
  22. [latex]\Large\frac{8\cdot 9 - 7\cdot 6}{5\cdot 6 - 9\cdot 2}[/latex]

  23. [latex]\Large\frac{{5}^{2}-{3}^{2}}{3 - 5}[/latex]
  24. [latex]\Large\frac{{6}^{2}-{4}^{2}}{4 - 6}[/latex]

  25. [latex]\Large\frac{2+4\left(3\right)}{-3-{2}^{2}}[/latex]
  26. [latex]\Large\frac{7+3\left(5\right)}{-2-{3}^{2}}[/latex]

  27. [latex]\Large\frac{7\cdot 4 - 2\left(8 - 5\right)}{9.3 - 3.5}[/latex]
  28. [latex]\Large\frac{9\cdot 7 - 3\left(12 - 8\right)}{8.7 - 6.6}[/latex]

  29. [latex]\Large\frac{9\left(8 - 2\right)-3\left(15 - 7\right)}{6\left(7 - 1\right)-3\left(17 - 9\right)}[/latex]
  30. [latex]\Large\frac{8\left(9 - 2\right)-4\left(14 - 9\right)}{7\left(8 - 3\right)-3\left(16 - 9\right)}[/latex]

Everyday Math

Baking

A recipe for chocolate chip cookies calls for [latex]2\Large\frac{1}{4}[/latex] cups of flour. Graciela wants to double the recipe.

  1.  How much flour will Graciela need? Show your calculation. Write your result as an improper fraction and as a mixed number.
  2. Measuring cups usually come in sets with cups for [latex]\Large\frac{1}{8},\Large\frac{1}{4},\Large\frac{1}{3},\Large\frac{1}{2}\normalsize ,\text{ and }1[/latex] cup. Draw a diagram to show two different ways that Graciela could measure out the flour needed to double the recipe.

Baking

A booth at the county fair sells fudge by the pound. Their award winning “Chocolate Overdose” fudge contains [latex]2\Large\frac{2}{3}[/latex] cups of chocolate chips per pound.

  1. How many cups of chocolate chips are in a half-pound of the fudge

  2. The owners of the booth make the fudge in [latex]10[/latex] -pound batches. How many chocolate chips do they need to make a [latex]10[/latex] -pound batch? Write your results as improper fractions and as a mixed numbers.

Writing Exercises

Explain how to find the reciprocal of a mixed number.

Explain how to multiply mixed numbers.

Randy thinks that [latex]3\Large\frac{1}{2}\normalsize\cdot 5\Large\frac{1}{4}[/latex] is [latex]15\Large\frac{1}{8}[/latex]. Explain what is wrong with Randy’s thinking.

Explain why [latex]-\Large\frac{1}{2},\Large\frac{-1}{2}[/latex], and [latex]\Large\frac{1}{-2}[/latex] are equivalent.

Adding and Subtracting Fractions With Common Denominators

Model Fraction Addition

In the following exercises, use a model to add the fractions. Show a diagram to illustrate your model.

  1. [latex]\Large\frac{2}{5}+\Large\frac{1}{5}[/latex]
  2. [latex]\Large\frac{3}{10}+\Large\frac{4}{10}[/latex]

  3. [latex]\Large\frac{7}{10}[/latex]
  4. [latex]\Large\frac{1}{6}+\Large\frac{3}{6}[/latex]
  5. [latex]\Large\frac{3}{8}+\Large\frac{3}{8}[/latex]

  6. [latex]\Large\frac{3}{4}[/latex]

Add Fractions with a Common Denominator

In the following exercises, find each sum.

  1. [latex]\Large\frac{4}{9}+\Large\frac{1}{9}[/latex]
  2. [latex]\Large\frac{2}{9}+\Large\frac{5}{9}[/latex]

  3. [latex]\Large\frac{6}{13}+\Large\frac{7}{13}[/latex]
  4. [latex]\Large\frac{9}{15}+\Large\frac{7}{15}[/latex]

  5. [latex]\Large\frac{x}{4}+\Large\frac{3}{4}[/latex]
  6. [latex]\Large\frac{y}{3}+\Large\frac{2}{3}[/latex]

  7. [latex]\Large\frac{7}{p}+\Large\frac{9}{p}[/latex]
  8. [latex]\Large\frac{8}{q}+\Large\frac{6}{q}[/latex]

  9. [latex]\Large\frac{8b}{9}+\Large\frac{3b}{9}[/latex]
  10. [latex]\Large\frac{5a}{7}+\Large\frac{4a}{7}[/latex]

  11. [latex]\Large\frac{-12y}{8}+\Large\frac{3y}{8}[/latex]
  12. [latex]\Large\frac{-11x}{5}+\Large\frac{7x}{5}[/latex]

  13. [latex]-\Large\frac{1}{8}+\Large\left(-\frac{3}{8}\right)[/latex]
  14. [latex]-\Large\frac{1}{8}+\Large\left(-\frac{5}{8}\right)[/latex]

  15. [latex]-\Large\frac{3}{16}+\Large\left(-\frac{7}{16}\right)[/latex]
  16. [latex]-\Large\frac{5}{16}+\Large\left(-\frac{9}{16}\right)[/latex]

  17. [latex]-\Large\frac{8}{17}+\Large\frac{15}{17}[/latex]
  18. [latex]-\Large\frac{9}{19}+\Large\frac{17}{19}[/latex]

  19. [latex]\Large\frac{6}{13}+\Large\left(-\frac{10}{13}\right)+\Large\left(-\frac{12}{13}\right)[/latex]
  20. [latex]\Large\frac{5}{12}+\Large\left(-\frac{7}{12}\right)+\Large\left(-\frac{11}{12}\right)[/latex]

Model Fraction Subtraction

In the following exercises, use a model to subtract the fractions. Show a diagram to illustrate your model.

  1. [latex]\Large\frac{5}{8}-\Large\frac{2}{8}[/latex]
  2. [latex]\Large\frac{5}{6}-\Large\frac{2}{6}[/latex]

  3. [latex]\Large\frac{1}{2}[/latex]

Subtract Fractions with a Common Denominator

In the following exercises, find the difference.

  1. [latex]\Large\frac{4}{5}-\Large\frac{1}{5}[/latex]
  2. [latex]\Large\frac{4}{5}-\Large\frac{3}{5}[/latex]

  3. [latex]\Large\frac{11}{15}-\Large\frac{7}{15}[/latex]
  4. [latex]\Large\frac{9}{13}-\Large\frac{4}{13}[/latex]

  5. [latex]\Large\frac{11}{12}-\Large\frac{5}{12}[/latex]
  6. [latex]\Large\frac{7}{12}-\Large\frac{5}{12}[/latex]

  7. [latex]\Large\frac{4}{21}-\Large\frac{19}{21}[/latex]
  8. [latex]-\Large\frac{8}{9}-\Large\frac{16}{9}[/latex]

  9. [latex]\Large\frac{y}{17}-\Large\frac{9}{17}[/latex]
  10. [latex]\Large\frac{x}{19}-\Large\frac{8}{19}[/latex]

  11. [latex]\Large\frac{5y}{8}-\Large\frac{7}{8}[/latex]
  12. [latex]\Large\frac{11z}{13}-\Large\frac{8}{13}[/latex]

  13. [latex]-\Large\frac{8}{d}-\Large\frac{3}{d}[/latex]
  14. [latex]-\Large\frac{7}{c}-\Large\frac{7}{c}[/latex]

  15. [latex]-\Large\frac{23}{u}-\Large\frac{15}{u}[/latex]
  16. [latex]-\Large\frac{29}{v}-\Large\frac{26}{v}[/latex]

  17. [latex]\Large\frac{6c}{7}-\Large\frac{5c}{7}[/latex]
  18. [latex]\Large\frac{12d}{11}-\Large\frac{9d}{11}[/latex]

  19. [latex]\Large\frac{-4r}{13}-\Large\frac{5r}{13}[/latex]
  20. [latex]\Large\frac{-7s}{3}-\Large\frac{7s}{3}[/latex]

  21. [latex]-\Large\frac{3}{5}-\Large\left(-\frac{4}{5}\right)[/latex]
  22. [latex]-\Large\frac{3}{7}-\Large\left(-\frac{5}{7}\right)[/latex]

  23. [latex]-\Large\frac{7}{9}-\Large\left(-\frac{5}{9}\right)[/latex]
  24. [latex]-\Large\frac{8}{11}-\Large\left(-\frac{5}{11}\right)[/latex]

Mixed Practice

In the following exercises, perform the indicated operation and write your answers in simplified form.

  1. [latex]-\Large\frac{5}{18}\cdot\Large\frac{9}{10}[/latex]
  2. [latex]-\Large\frac{3}{14}\cdot\Large\frac{7}{12}[/latex]

  3. [latex]\Large\frac{n}{5}-\Large\frac{4}{5}[/latex]
  4. [latex]\Large\frac{6}{11}-\Large\frac{s}{11}[/latex]

  5. [latex]-\Large\frac{7}{24}+\Large\frac{2}{24}[/latex]
  6. [latex]-\Large\frac{5}{18}+\Large\frac{1}{18}[/latex]

  7. [latex]\Large\frac{8}{15}\div\Large\frac{12}{5}[/latex]
  8. [latex]\Large\frac{7}{12}\div\Large\frac{9}{28}[/latex]

Everyday Math

Trail Mix

Jacob is mixing together nuts and raisins to make trail mix. He has [latex]\Large\frac{6}{10}[/latex] of a pound of nuts and [latex]\Large\frac{3}{10}[/latex] of a pound of raisins. How much trail mix can he make?

Baking

Janet needs [latex]\Large\frac{5}{8}[/latex] of a cup of flour for a recipe she is making. She only has [latex]\Large\frac{3}{8}[/latex] of a cup of flour and will ask to borrow the rest from her next-door neighbor. How much flour does she have to borrow?

Writing Exercises

Greg dropped his case of drill bits and three of the bits fell out. The case has slots for the drill bits, and the slots are arranged in order from smallest to largest. Greg needs to put the bits that fell out back in the case in the empty slots. Where do the three bits go? Explain how you know.

Bits in case: [latex]\Large\frac{1}{16}[/latex] , [latex]\Large\frac{1}{8}[/latex] , ___, ___, [latex]\Large\frac{5}{16}[/latex] , [latex]\Large\frac{3}{8}[/latex] , ___, [latex]\Large\frac{1}{2}[/latex] , [latex]\Large\frac{9}{16}[/latex] , [latex]\Large\frac{5}{8}[/latex] .

After a party, Lupe has [latex]\Large\frac{5}{12}[/latex] of a cheese pizza, [latex]\Large\frac{4}{12}[/latex] of a pepperoni pizza, and [latex]\Large\frac{4}{12}[/latex] of a veggie pizza left. Will all the slices fit into [latex]1[/latex] pizza box? Explain your reasoning.

Adding and Subtracting Fractions with Different Denominators

Find the Least Common Denominator (LCD)

In the following exercises, find the least common denominator (LCD) for each set of fractions.

  1. [latex]\Large\frac{2}{3}\normalsize\text{ and }\Large\frac{3}{4}[/latex]
  2. [latex]\Large\frac{3}{4}\normalsize\text{ and }\Large\frac{2}{5}[/latex]

  3. [latex]\Large\frac{7}{12}\normalsize\text{ and }\Large\frac{5}{8}[/latex]
  4. [latex]\Large\frac{9}{16}\normalsize\text{ and }\Large\frac{7}{12}[/latex]

  5. [latex]\Large\frac{13}{30}\normalsize\text{ and }\Large\frac{25}{42}[/latex]
  6. [latex]\Large\frac{23}{30}\normalsize\text{ and }\Large\frac{5}{48}[/latex]

  7. [latex]\Large\frac{21}{35}\normalsize\text{ and }\Large\frac{39}{56}[/latex]
  8. [latex]\Large\frac{18}{35}\normalsize\text{ and }\Large\frac{33}{49}[/latex]

  9. [latex]\Large\frac{2}{3}\normalsize\text{,}\Large\frac{1}{6}\normalsize,\text{ and }\Large\frac{3}{4}[/latex]
  10. [latex]\Large\frac{2}{3}\normalsize\text{,}\Large\frac{1}{4}\normalsize,\text{ and }\Large\frac{3}{5}[/latex]

Convert Fractions to Equivalent Fractions with the LCD

In the following exercises, convert to equivalent fractions using the LCD.

  1. [latex]\Large\frac{1}{3}\normalsize\text{ and }\Large\frac{1}{4}\normalsize,\text{LCD}=12[/latex]
  2. [latex]\Large\frac{1}{4}\normalsize\text{ and }\Large\frac{1}{5}\normalsize,\text{LCD}=20[/latex]

  3. [latex]\Large\frac{5}{12}\normalsize\text{ and }\Large\frac{7}{8}\normalsize,\text{LCD}=24[/latex]
  4. [latex]\Large\frac{7}{12}\normalsize\text{ and }\Large\frac{5}{8}\normalsize,\text{LCD}=24[/latex]

  5. [latex]\Large\frac{13}{16}\normalsize\text{ and }\text{-}\Large\frac{11}{12}\normalsize,\text{LCD}=48[/latex]
  6. [latex]\Large\frac{11}{16}\normalsize\text{ and }\text{-}\Large\frac{5}{12}\normalsize,\text{LCD}=48[/latex]

  7. [latex]\Large\frac{1}{3},\Large\frac{5}{6}\normalsize,\text{ and }\Large\frac{3}{4}\normalsize,\text{LCD}=12[/latex]
  8. [latex]\Large\frac{1}{3},\Large\frac{3}{4}\normalsize,\text{ and }\Large\frac{3}{5}\normalsize,\text{LCD}=60[/latex]

Add and Subtract Fractions with Different Denominators

In the following exercises, add or subtract. Write the result in simplified form.

  1. [latex]\Large\frac{1}{3}+\Large\frac{1}{5}[/latex]
  2. [latex]\Large\frac{1}{4}+\Large\frac{1}{5}[/latex]

  3. [latex]\Large\frac{1}{2}+\Large\frac{1}{7}[/latex]
  4. [latex]\Large\frac{1}{3}+\Large\frac{1}{8}[/latex]

  5. [latex]\Large\frac{1}{3}-\Large\left(-\frac{1}{9}\right)[/latex]
  6. [latex]\Large\frac{1}{4}-\Large\left(-\frac{1}{8}\right)[/latex]

  7. [latex]\Large\frac{1}{5}-\Large\left(-\frac{1}{10}\right)[/latex]
  8. [latex]\Large\frac{1}{2}-\Large\left(-\frac{1}{6}\right)[/latex]

  9. [latex]\Large\frac{2}{3}+\Large\frac{3}{4}[/latex]
  10. [latex]\Large\frac{3}{4}+\Large\frac{2}{5}[/latex]

  11. [latex]\Large\frac{7}{12}+\Large\frac{5}{8}[/latex]
  12. [latex]\Large\frac{5}{12}+\Large\frac{3}{8}[/latex]

  13. [latex]\Large\frac{7}{12}-\Large\frac{9}{16}[/latex]
  14. [latex]\Large\frac{7}{16}-\Large\frac{5}{12}[/latex]

  15. [latex]\Large\frac{11}{12}-\Large\frac{3}{8}[/latex]
  16. [latex]\Large\frac{5}{8}-\Large\frac{7}{12}[/latex]

  17. [latex]\Large\frac{2}{3}-\Large\frac{3}{8}[/latex]
  18. [latex]\Large\frac{5}{6}-\Large\frac{3}{4}[/latex]

  19. [latex]-\Large\frac{11}{30}+\Large\frac{27}{40}[/latex]
  20. [latex]-\Large\frac{9}{20}+\Large\frac{17}{30}[/latex]

  21. [latex]-\Large\frac{13}{30}+\Large\frac{25}{42}[/latex]
  22. [latex]-\Large\frac{23}{30}+\Large\frac{5}{48}[/latex]

  23. [latex]-\Large\frac{39}{56}-\Large\frac{22}{35}[/latex]
  24. [latex]-\Large\frac{33}{49}-\Large\frac{18}{35}[/latex]

  25. [latex]-\Large\frac{2}{3}-\Large\left(-\frac{3}{4}\right)[/latex]
  26. [latex]-\Large\frac{3}{4}-\Large\left(-\frac{4}{5}\right)[/latex]

  27. [latex]-\Large\frac{9}{16}-\Large\left(-\frac{4}{5}\right)[/latex]
  28. [latex]-\Large\frac{7}{20}-\Large\left(-\frac{5}{8}\right)[/latex]

  29. [latex]1+\Large\frac{7}{8}[/latex]
  30. [latex]1+\Large\frac{5}{6}[/latex]

  31. [latex]1-\Large\frac{5}{9}[/latex]
  32. [latex]1-\Large\frac{3}{10}[/latex]

  33. [latex]\Large\frac{x}{3}+\Large\frac{1}{4}[/latex]
  34. [latex]\Large\frac{y}{2}+\Large\frac{2}{3}[/latex]

  35. [latex]\Large\frac{y}{4}-\Large\frac{3}{5}[/latex]
  36. [latex]\Large\frac{x}{5}-\Large\frac{1}{4}[/latex]

Identify and Use Fraction Operations

In the following exercises, perform the indicated operations. Write your answers in simplified form.

  1. [latex]\Large\frac{3}{4}+\Large\frac{1}{6}[/latex]
  2. [latex]\Large\frac{3}{4}\div\Large\frac{1}{6}[/latex]
  3. [latex]\Large\frac{2}{3}+\Large\frac{1}{6}[/latex]

  4. [latex]\Large\frac{2}{3}\div\Large\frac{1}{6}[/latex]

  5. [latex]\text{-}\Large\frac{2}{5}-\Large\frac{1}{8}[/latex]
  6. [latex]\text{-}\Large\frac{2}{5}\cdot\Large\frac{1}{8}[/latex]
  7. [latex]\text{-}\Large\frac{4}{5}-\Large\frac{1}{8}[/latex]

  8. [latex]\text{-}\Large\frac{4}{5}\cdot\Large\frac{1}{8}[/latex]

  9. [latex]\Large\frac{5}{n}\div\Large\frac{8}{15}[/latex]
  10. [latex]\Large\frac{5}{n}-\Large\frac{8}{15}[/latex]
  11. [latex]\Large\frac{3}{a}\div\Large\frac{7}{12}[/latex]

  12. [latex]\Large\frac{3}{a}-\Large\frac{7}{12}[/latex]

  13. [latex]\Large\frac{9}{10}\cdot\Large\left(-\frac{11}{d}\right)[/latex]
  14. [latex]\Large\frac{9}{10}+\Large\left(-\frac{11}{d}\right)[/latex]
  15. [latex]\Large\frac{4}{15}\cdot\Large\left(-\frac{5}{q}\right)[/latex]

  16. [latex]\Large\frac{4}{15}+\Large\left(-\frac{5}{q}\right)[/latex]

  17. [latex]-\Large\frac{3}{8}\div\Large\left(-\frac{3}{10}\right)[/latex]
  18. [latex]-\Large\frac{5}{12}\div\Large\left(-\frac{5}{9}\right)[/latex]
  19. [latex]-\Large\frac{3}{8}+\Large\frac{5}{12}[/latex]
  20. [latex]-\Large\frac{1}{8}+\Large\frac{7}{12}[/latex]

  21. [latex]\Large\frac{5}{6}-\Large\frac{1}{9}[/latex]
  22. [latex]\Large\frac{5}{9}-\Large\frac{1}{6}[/latex]

  23. [latex]\Large\frac{3}{8}\cdot\Large\left(-\frac{10}{21}\right)[/latex]
  24. [latex]\Large\frac{7}{12}\cdot\Large\left(-\frac{8}{35}\right)[/latex]

  25. [latex]-\Large\frac{7}{15}-\Large\frac{y}{4}[/latex]
  26. [latex]-\Large\frac{3}{8}-\Large\frac{x}{11}[/latex]

  27. [latex]\Large\frac{11}{12a}\cdot\Large\frac{9a}{16}[/latex]
  28. [latex]\Large\frac{10y}{13}\cdot\Large\frac{8}{15y}[/latex]

Use the Order of Operations to Simplify Complex Fractions

In the following exercises, simplify.

  1. [latex]\displaystyle\frac{{\Large\left(\frac{1}{5}\right)}^{2}}{2+{3}^{2}}[/latex]
  2. [latex]\displaystyle\frac{{\Large\left(\frac{1}{3}\right)}^{2}}{5+{2}^{2}}[/latex]

  3. [latex]\displaystyle\frac{{2}^{3}+{4}^{2}}{{\Large\left(\frac{2}{3}\right)}^{2}}[/latex]
  4. [latex]\displaystyle\frac{{3}^{3}-{3}^{2}}{{\Large\left(\frac{3}{4}\right)}^{2}}[/latex]

  5. [latex]\displaystyle\frac{{\Large\left(\frac{3}{5}\right)}^{2}}{{\Large\left(\frac{3}{7}\right)}^{2}}[/latex]
  6. [latex]\displaystyle\frac{{\Large\left(\frac{3}{4}\right)}^{2}}{{\Large\left(\frac{5}{8}\right)}^{2}}[/latex]

  7. [latex]\displaystyle\frac{2}{\Large\frac{1}{3}+\frac{1}{5}}[/latex]
  8. [latex]\displaystyle\frac{5}{\Large\frac{1}{4}+\frac{1}{3}}[/latex]

  9. [latex]\displaystyle\frac{\Large\frac{2}{3}+\frac{1}{2}}{\Large\frac{3}{4}-\frac{2}{3}}[/latex]
  10. [latex]\displaystyle\frac{\Large\frac{3}{4}+\frac{1}{2}}{\Large\frac{5}{6}-\frac{2}{3}}[/latex]

  11. [latex]\displaystyle\frac{\Large\frac{7}{8}-\frac{2}{3}}{\Large\frac{1}{2}+\frac{3}{8}}[/latex]
  12. [latex]\displaystyle\frac{\Large\frac{3}{4}-\frac{3}{5}}{\Large\frac{1}{4}+\frac{2}{5}}[/latex]

Mixed Practice

In the following exercises, simplify.

  1. [latex]\Large\frac{1}{2}+\frac{2}{3}\cdot \frac{5}{12}[/latex]
  2. [latex]\Large\frac{1}{3}+\frac{2}{5}\cdot \frac{3}{4}[/latex]

  3. [latex]1-\Large\frac{3}{5}\div \frac{1}{10}[/latex]
  4. [latex]1-\Large\frac{5}{6}\div \frac{1}{12}[/latex]

  5. [latex]\Large\frac{2}{3}+\frac{1}{6}+\frac{3}{4}[/latex]
  6. [latex]\Large\frac{2}{3}+\frac{1}{4}+\frac{3}{5}[/latex]

  7. [latex]\Large\frac{3}{8}-\frac{1}{6}+\frac{3}{4}[/latex]
  8. [latex]\Large\frac{2}{5}+\frac{5}{8}-\frac{3}{4}[/latex]

  9. [latex]12\Large\left(\frac{9}{20}-\frac{4}{15}\right)[/latex]
  10. [latex]8\Large\left(\frac{15}{16}-\frac{5}{6}\right)[/latex]

  11. [latex]\Large\frac{\LARGE\frac{5}{8}+\LARGE\frac{1}{6}}{\LARGE\frac{19}{24}}[/latex]
  12. [latex]\LARGE\frac{\LARGE\frac{1}{6}+\LARGE\frac{3}{10}}{\LARGE\frac{14}{30}}[/latex]

  13. [latex]\Large\left(\frac{5}{9}+\frac{1}{6}\right)\div \left(\frac{2}{3}-\frac{1}{2}\right)[/latex]
  14. [latex]\Large\left(\frac{3}{4}+\frac{1}{6}\right)\div \left(\frac{5}{8}-\frac{1}{3}\right)[/latex]

Mixed Practice

In the following exercises, evaluate the given expression. Express your answers in simplified form, using improper fractions if necessary.

Exercise 1

[latex]x+\Large\frac{1}{2}[/latex] when

  1. [latex]x=-\Large\frac{1}{8}[/latex]
  2. [latex]x=-\Large\frac{1}{2}[/latex]

Exercise 2

[latex]x+\Large\frac{2}{3}[/latex] when

  1. [latex]x=-\Large\frac{1}{6}[/latex]
  2. [latex]x=-\Large\frac{5}{3}[/latex]

Exercise 3

[latex]x+\Large\left(-\frac{5}{6}\right)[/latex] when

  1. [latex]x=\Large\frac{1}{3}[/latex]
  2. [latex]x=-\Large\frac{1}{6}[/latex]

Exercise 4

[latex]x+\Large\left(-\frac{11}{12}\right)[/latex] when

  1. [latex]x=\Large\frac{11}{12}[/latex]
  2. [latex]x=\Large\frac{3}{4}[/latex]

Exercise 5

[latex]x-\Large\frac{2}{5}[/latex] when

  1. [latex]x=\Large\frac{3}{5}[/latex]
  2. [latex]x=-\Large\frac{3}{5}[/latex]

Exercise 6

[latex]x-\Large\frac{1}{3}[/latex] when

  1. [latex]x=\Large\frac{2}{3}[/latex]
  2. [latex]x=-\Large\frac{2}{3}[/latex]

Exercise 7

[latex]\Large\frac{7}{10}\normalsize-w[/latex] when

  1. [latex]w=\Large\frac{1}{2}[/latex]
  2. [latex]w=-\Large\frac{1}{2}[/latex]

Exercise 8

[latex]\Large\frac{5}{12}\normalsize-w[/latex] when

  1. [latex]w=\Large\frac{1}{4}[/latex]
  2. [latex]w=-\Large\frac{1}{4}[/latex]

Mixed Practice

In the following exercises, evaluate the given expression. Express your answers in simplified form, using improper fractions if necessary.

  1. [latex]4{p}^{2}q[/latex] when [latex]p=-\Large\frac{1}{2}\normalsize\text{ and }q=\Large\frac{5}{9}[/latex]
  2. [latex]5{m}^{2}n\text{ when }m=-\Large\frac{2}{5}\normalsize\text{ and }n=\Large\frac{1}{3}[/latex]

  3. [latex]2{x}^{2}{y}^{3}\text{ when }x=-\Large\frac{2}{3}\normalsize\text{ and }y=-\Large\frac{1}{2}[/latex]
  4. [latex]8{u}^{2}{v}^{3}\text{ when }u=-\Large\frac{3}{4}\normalsize\text{ and }v=-\Large\frac{1}{2}[/latex]

  5. [latex]\Large\frac{u+v}{w}\normalsize\text{ when }u=-4,v=-8,w=2[/latex]
  6. [latex]\Large\frac{m+n}{p}\normalsize\text{ when }m=-6,n=-2,p=4[/latex]

  7. [latex]\Large\frac{a+b}{a-b}\normalsize\text{ when }a=-3,b=8[/latex]
  8. [latex]\Large\frac{r-s}{r+s}\normalsize\text{ when }r=10,s=-5[/latex]

Everyday Math

Decorating

Laronda is making covers for the throw pillows on her sofa. For each pillow cover, she needs [latex]\Large\frac{3}{16}[/latex] yard of print fabric and [latex]\Large\frac{3}{8}[/latex] yard of solid fabric. What is the total amount of fabric Laronda needs for each pillow cover?

Baking

Vanessa is baking chocolate chip cookies and oatmeal cookies. She needs [latex]1\Large\frac{1}{4}[/latex] cups of sugar for the chocolate chip cookies, and [latex]1\Large\frac{1}{8}[/latex] cups for the oatmeal cookies How much sugar does she need altogether?

Writing Exercises

Explain why it is necessary to have a common denominator to add or subtract fractions.

Explain how to find the LCD of two fractions.

Adding and Subtracting Mixed Numbers

Model Addition of Mixed Numbers

In the following exercises, use a model to find the sum. Draw a picture to illustrate your model.

  1. [latex]1\Large\frac{1}{5}\normalsize+3\Large\frac{1}{5}[/latex]
  2. [latex]2\Large\frac{1}{3}\normalsize+1\Large\frac{1}{3}[/latex]

  3. [latex]3\Large\frac{2}{3}[/latex]
  4. [latex]1\Large\frac{3}{8}\normalsize+1\Large\frac{7}{8}[/latex]
  5. [latex]1\Large\frac{5}{6}\normalsize+1\Large\frac{5}{6}[/latex]

  6. [latex]3\Large\frac{2}{3}[/latex]

Add Mixed Numbers with a Common Denominator

In the following exercises, add.

  1. [latex]5\Large\frac{1}{3}\normalsize+6\Large\frac{1}{3}[/latex]
  2. [latex]2\Large\frac{4}{9}\normalsize+5\Large\frac{1}{9}[/latex]

  3. [latex]4\Large\frac{5}{8}\normalsize+9\Large\frac{3}{8}[/latex]
  4. [latex]7\Large\frac{9}{10}\normalsize+3\Large\frac{1}{10}[/latex]

  5. [latex]3\Large\frac{4}{5}\normalsize+6\Large\frac{4}{5}[/latex]
  6. [latex]9\Large\frac{2}{3}\normalsize+1\Large\frac{2}{3}[/latex]

  7. [latex]6\Large\frac{9}{10}\normalsize+8\Large\frac{3}{10}[/latex]
  8. [latex]8\Large\frac{4}{9}\normalsize+2\Large\frac{8}{9}[/latex]

Model Subtraction of Mixed Numbers

In the following exercises, use a model to find the difference. Draw a picture to illustrate your model.

  1. [latex]1\Large\frac{1}{6}-\Large\frac{5}{6}[/latex]
  2. [latex]1\Large\frac{1}{8}-\Large\frac{5}{8}[/latex]

  3. [latex]\Large\frac{1}{2}[/latex]

Subtract Mixed Numbers with a Common Denominator

In the following exercises, find the difference.

  1. [latex]2\Large\frac{7}{8}\normalsize-1\Large\frac{3}{8}[/latex]
  2. [latex]2\Large\frac{7}{12}\normalsize-1\Large\frac{5}{12}[/latex]

  3. [latex]8\Large\frac{17}{20}\normalsize-4\Large\frac{9}{20}[/latex]
  4. [latex]19\Large\frac{13}{15}\normalsize-13\Large\frac{7}{15}[/latex]

  5. [latex]8\Large\frac{3}{7}\normalsize-4\Large\frac{4}{7}[/latex]
  6. [latex]5\Large\frac{2}{9}\normalsize-3\Large\frac{4}{9}[/latex]

  7. [latex]2\Large\frac{5}{8}\normalsize-1\Large\frac{7}{8}[/latex]
  8. [latex]2\Large\frac{5}{12}\normalsize-1\Large\frac{7}{12}[/latex]

Add and Subtract Mixed Numbers with Different Denominators

In the following exercises, write the sum or difference as a mixed number in simplified form.

  1. [latex]3\Large\frac{1}{4}\normalsize+6\Large\frac{1}{3}[/latex]
  2. [latex]2\Large\frac{1}{6}\normalsize+5\Large\frac{3}{4}[/latex]

  3. [latex]1\Large\frac{5}{8}\normalsize+4\Large\frac{1}{2}[/latex]
  4. [latex]7\Large\frac{2}{3}\normalsize+8\Large\frac{1}{2}[/latex]

  5. [latex]9\Large\frac{7}{10}\normalsize-2\Large\frac{1}{3}[/latex]
  6. [latex]6\Large\frac{4}{5}\normalsize-1\Large\frac{1}{4}[/latex]

  7. [latex]2\Large\frac{2}{3}\normalsize-3\Large\frac{1}{2}[/latex]
  8. [latex]2\Large\frac{7}{8}\normalsize-4\Large\frac{1}{3}[/latex]

Mixed Practice

In the following exercises, perform the indicated operation and write the result as a mixed number in simplified form.

  1. [latex]2\Large\frac{5}{8}\normalsize\cdot 1\Large\frac{3}{4}[/latex]
  2. [latex]1\Large\frac{2}{3}\normalsize\cdot 4\Large\frac{1}{6}[/latex]

  3. [latex]\Large\frac{2}{7}+\Large\frac{4}{7}[/latex]
  4. [latex]\Large\frac{2}{9}+\Large\frac{5}{9}[/latex]

  5. [latex]1\Large\frac{5}{12}\div\Large\frac{1}{12}[/latex]
  6. [latex]2\Large\frac{3}{10}\div\Large\frac{1}{10}[/latex]

  7. [latex]13\Large\frac{5}{12}\normalsize-9\Large\frac{7}{12}[/latex]
  8. [latex]15\Large\frac{5}{8}\normalsize-6\Large\frac{7}{8}[/latex]

  9. [latex]\Large\frac{5}{9}-\Large\frac{4}{9}[/latex]
  10. [latex]\Large\frac{11}{15}-\Large\frac{7}{15}[/latex]

  11. [latex]4-\Large\frac{3}{4}[/latex]
  12. [latex]6-\Large\frac{2}{5}[/latex]

  13. [latex]\Large\frac{9}{20}\div\Large\frac{3}{4}[/latex]
  14. [latex]\Large\frac{7}{24}\div\Large\frac{14}{3}[/latex]

  15. [latex]9\Large\frac{6}{11}\normalsize+7\Large\frac{10}{11}[/latex]
  16. [latex]8\Large\frac{5}{13}\normalsize+4\Large\frac{9}{13}[/latex]

  17. [latex]3\Large\frac{2}{5}\normalsize+5\Large\frac{3}{4}[/latex]
  18. [latex]2\Large\frac{5}{6}\normalsize+4\Large\frac{1}{5}[/latex]

  19. [latex]\Large\frac{8}{15}\cdot\Large\frac{10}{19}[/latex]
  20. [latex]\Large\frac{5}{12}\cdot\Large\frac{8}{9}[/latex]

  21. [latex]6\Large\frac{7}{8}\normalsize-2\Large\frac{1}{3}[/latex]
  22. [latex]6\Large\frac{5}{9}\normalsize-4\Large\frac{2}{5}[/latex]

  23. [latex]5\Large\frac{2}{9}\normalsize-4\Large\frac{4}{5}[/latex]
  24. [latex]4\Large\frac{3}{8}\normalsize-3\Large\frac{2}{3}[/latex]

Everyday Math

Sewing

Renata is sewing matching shirts for her husband and son. According to the patterns she will use, she needs [latex]2\Large\frac{3}{8}[/latex] yards of fabric for her husband’s shirt and [latex]1\Large\frac{1}{8}[/latex] yards of fabric for her son’s shirt. How much fabric does she need to make both shirts?

Sewing

Pauline has [latex]3\Large\frac{1}{4}[/latex] yards of fabric to make a jacket. The jacket uses [latex]2\Large\frac{2}{3}[/latex] yards. How much fabric will she have left after making the jacket?

Printing

Nishant is printing invitations on his computer. The paper is [latex]8\Large\frac{1}{2}[/latex] inches wide, and he sets the print area to have a [latex]1\Large\frac{1}{2}[/latex] -inch border on each side. How wide is the print area on the sheet of paper?

Framing a picture

Tessa bought a picture frame for her son’s graduation picture. The picture is [latex]8[/latex] inches wide. The picture frame is [latex]2\Large\frac{5}{8}[/latex] inches wide on each side. How wide will the framed picture be?

Writing Exercises

Draw a diagram and use it to explain how to add [latex]1\Large\frac{5}{8}\normalsize+2\Large\frac{7}{8}[/latex].

Edgar will have to pay [latex]\$3.75[/latex] in tolls to drive to the city.

  1. Explain how he can make change from a [latex]\$10[/latex] bill before he leaves so that he has the exact amount he needs.
  2. How is Edgar’s situation similar to how you subtract [latex]10 - 3\Large\frac{3}{4}?[/latex]

Add [latex]4\Large\frac{5}{12}\normalsize+3\Large\frac{7}{8}[/latex] twice, first by leaving them as mixed numbers and then by rewriting as improper fractions. Which method do you prefer, and why?

Subtract [latex]3\Large\frac{7}{8}\normalsize-4\Large\frac{5}{12}[/latex] twice, first by leaving them as mixed numbers and then by rewriting as improper fractions. Which method do you prefer, and why?

Solving Equations That Contain Fractions

Determine Whether a Fraction is a Solution of an Equation

In the following exercises, determine whether each number is a solution of the given equation.

Exercise 1

[latex]x-\Large\frac{2}{5}=\Large\frac{1}{10}\normalsize\text{:}[/latex]

  1. [latex]x=1[/latex]
  2. [latex]x=\Large\frac{1}{2}[/latex]
  3. [latex]x=-\Large\frac{1}{2}[/latex]

Exercise 2

[latex]y-\Large\frac{1}{3}=\Large\frac{5}{12}\normalsize\text{:}[/latex]

  1. [latex]y=1[/latex]
  2. [latex]y=\Large\frac{3}{4}[/latex]
  3. [latex]y=-\Large\frac{3}{4}[/latex]

Exercise 3

[latex]h+\Large\frac{3}{4}=\Large\frac{2}{5}\normalsize\text{:}[/latex]

  1. [latex]h=1[/latex]
  2. [latex]h=\Large\frac{7}{20}[/latex]
  3. [latex]h=-\Large\frac{7}{20}[/latex]

Exercise 4

[latex]k+\Large\frac{2}{5}=\Large\frac{5}{6}\normalsize\text{:}[/latex]

  1. [latex]k=1[/latex]
  2. [latex]k=\Large\frac{13}{30}[/latex]
  3. [latex]k=-\Large\frac{13}{30}[/latex]

Solve Equations with Fractions using the Addition, Subtraction, and Division Properties of Equality

In the following exercises, solve.

  1. [latex]y+\Large\frac{1}{3}=\Large\frac{4}{3}[/latex]
  2. [latex]m+\Large\frac{3}{8}=\Large\frac{7}{8}[/latex]

  3. [latex]f+\Large\frac{9}{10}=\Large\frac{2}{5}[/latex]
  4. [latex]h+\Large\frac{5}{6}=\Large\frac{1}{6}[/latex]

  5. [latex]a-\Large\frac{5}{8}=-\Large\frac{7}{8}[/latex]
  6. [latex]c-\Large\frac{1}{4}=-\Large\frac{5}{4}[/latex]

  7. [latex]x-\Large\left(-\frac{3}{20}\right)=-\Large\frac{11}{20}[/latex]
  8. [latex]z-\Large\left(-\frac{5}{12}\right)=-\Large\frac{7}{12}[/latex]

  9. [latex]n-\Large\frac{1}{6}=\Large\frac{3}{4}[/latex]
  10. [latex]p-\Large\frac{3}{10}=\Large\frac{5}{8}[/latex]

  11. [latex]s+\Large\left(-\frac{1}{2}\right)=-\Large\frac{8}{9}[/latex]
  12. [latex]k+\Large\left(-\frac{1}{3}\right)=-\Large\frac{4}{5}[/latex]

  13. [latex]5j=17[/latex]
  14. [latex]7k=18[/latex]

  15. [latex]-4w=26[/latex]
  16. [latex]-9v=33[/latex]

Solve Equations with Fractions Using the Multiplication Property of Equality

In the following exercises, solve.

  1. [latex]\Large\frac{f}{4}\normalsize=-20[/latex]
  2. [latex]\Large\frac{b}{3}\normalsize=-9[/latex]

  3. [latex]\Large\frac{y}{7}\normalsize=-21[/latex]
  4. [latex]\Large\frac{x}{8}\normalsize=-32[/latex]

  5. [latex]\Large\frac{p}{-5}\normalsize=-40[/latex]
  6. [latex]\Large\frac{q}{-4}\normalsize=-40[/latex]

  7. [latex]\Large\frac{r}{-12}\normalsize=-6[/latex]
  8. [latex]\Large\frac{s}{-15}\normalsize=-3[/latex]

  9. [latex]-x=23[/latex]
  10. [latex]-y=42[/latex]

  11. [latex]-h=-\Large\frac{5}{12}[/latex]
  12. [latex]-k=-\Large\frac{17}{20}[/latex]

  13. [latex]\Large\frac{4}{5}\normalsize n=20[/latex]
  14. [latex]\Large\frac{3}{10}\normalsize p=30[/latex]

  15. [latex]\Large\frac{3}{8}\normalsize q=-48[/latex]
  16. [latex]\Large\frac{5}{2}\normalsize m=-40[/latex]

  17. [latex]-\Large\frac{2}{9}\normalsize a=16[/latex]
  18. [latex]-\Large\frac{3}{7}\normalsize b=9[/latex]

  19. [latex]-\Large\frac{6}{11}\normalsize u=-24[/latex]
  20. [latex]-\Large\frac{5}{12}\normalsize v=-15[/latex]

Mixed Practice

In the following exercises, solve.

  1. [latex]3x=0[/latex]
  2. [latex]8y=0[/latex]

  3. [latex]4f=\Large\frac{4}{5}[/latex]
  4. [latex]7g=\Large\frac{7}{9}[/latex]

  5. [latex]p+\Large\frac{2}{3}=\Large\frac{1}{12}[/latex]
  6. [latex]q+\Large\frac{5}{6}=\Large\frac{1}{12}[/latex]

  7. [latex]\Large\frac{7}{8}\normalsize m=\Large\frac{1}{10}[/latex]
  8. [latex]\Large\frac{1}{4}\normalsize n=\Large\frac{7}{10}[/latex]

  9. [latex]-\Large\frac{2}{5}\normalsize=x+\Large\frac{3}{4}[/latex]
  10. [latex]-\Large\frac{2}{3}\normalsize=y+\Large\frac{3}{8}[/latex]

  11. [latex]\Large\frac{11}{20}\normalsize=\text{-}\mathit{\text{f}}[/latex]
  12. [latex]\Large\frac{8}{15}\normalsize=\text{-}\mathit{\text{d}}[/latex]

Translate Sentences to Equations and Solve

In the following exercises, translate to an algebraic equation and solve.

  1. [latex]n[/latex] divided by eight is [latex]-16[/latex].
  2. [latex]n[/latex] divided by six is [latex]-24[/latex].

  3. [latex]m[/latex] divided by [latex]-9[/latex] is [latex]-7[/latex].
  4. [latex]m[/latex] divided by [latex]-7[/latex] is [latex]-8[/latex].

  5. The quotient of [latex]f[/latex] and [latex]-3[/latex] is [latex]-18[/latex].
  6. The quotient of [latex]f[/latex] and [latex]-4[/latex] is [latex]-20[/latex].

  7. The quotient of [latex]g[/latex] and twelve is [latex]8[/latex].
  8. The quotient of [latex]g[/latex] and nine is [latex]14[/latex].

  9. Three-fourths of [latex]q[/latex] is [latex]12[/latex].
  10. Two-fifths of [latex]q[/latex] is [latex]20[/latex].

  11. Seven-tenths of [latex]p[/latex] is [latex]-63[/latex].
  12. Four-ninths of [latex]p[/latex] is [latex]-28[/latex].

  13. [latex]m[/latex] divided by [latex]4[/latex] equals negative [latex]6[/latex].
  14. The quotient of [latex]h[/latex] and [latex]2[/latex] is [latex]43[/latex].

  15. Three-fourths of [latex]z[/latex] is the same as [latex]15[/latex].
  16. The quotient of [latex]a[/latex] and [latex]\Large\frac{2}{3}[/latex] is [latex]\Large\frac{3}{4}[/latex].

  17. The sum of five-sixths and [latex]x[/latex] is [latex]\Large\frac{1}{2}[/latex].
  18. The sum of three-fourths and [latex]x[/latex] is [latex]\Large\frac{1}{8}[/latex].

  19. The difference of [latex]y[/latex] and one-fourth is [latex]-\Large\frac{1}{8}[/latex].
  20. The difference of [latex]y[/latex] and one-third is [latex]-\Large\frac{1}{6}[/latex].

Everyday Math

Shopping

Teresa bought a pair of shoes on sale for [latex]\$48[/latex]. The sale price was [latex]\Large\frac{2}{3}[/latex] of the regular price. Find the regular price of the shoes by solving the equation [latex]\Large\frac{2}{3}\normalsize p=48[/latex]

Playhouse

The table in a child’s playhouse is [latex]\Large\frac{3}{5}[/latex] of an adult-size table. The playhouse table is [latex]18[/latex] inches high. Find the height of an adult-size table by solving the equation [latex]\Large\frac{3}{5}\normalsize h=18[/latex].

Writing Exercises

There are three methods to solve the equation [latex]-y=15[/latex]. Which method do you prefer? Why?

Richard thinks the solution to the equation [latex]\Large\frac{3}{4}\normalsize x=24[/latex] is [latex]16[/latex]. Explain why Richard is wrong.

Chapter Review Exercises

Visualize Fractions

In the following exercises, name the fraction of each figure that is shaded.

Using Models to Represent Fractions

Exercise 1

A circle is shown. It is divided into 8 equal pieces. 5 pieces are shaded.

Exercise 2

A square is shown. It is divided into 9 equal pieces. 5 pieces are shaded.

Using Models to Represent Mixed Numbers

In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.

Exercise 1

Two squares are shown. Both are divided into four equal pieces. The square on the left has all 4 pieces shaded. The square on the right has one piece shaded.

Exercise 2

Two circles are shown. Both are divided into two equal pieces. The circle on the left has both pieces shaded. The circle on the right has one piece shaded.

Write an Improper Fraction as a Mixed Number

In the following exercises, convert the improper fraction to a mixed number.

  1. [latex]\Large\frac{58}{15}[/latex]
  2. [latex]\Large\frac{63}{11}[/latex]

Write a Mixed Number as an Improper Fraction

In the following exercises, convert the mixed number to an improper fraction.

  1. [latex]12\Large\frac{1}{4}[/latex]
  2. [latex]9\Large\frac{4}{5}[/latex]

  3. Find three fractions equivalent to [latex]\Large\frac{2}{5}[/latex]. Show your work, using figures or algebra.
  4. Find three fractions equivalent to [latex]-\Large\frac{4}{3}[/latex]. Show your work, using figures or algebra.

Locating Fractions on the Number Line

In the following exercises, locate the numbers on a number line.

  1. [latex]\Large\frac{5}{8},\Large\frac{4}{3},\normalsize 3\Large\frac{3}{4},\normalsize4[/latex]
  2. [latex]\Large\frac{1}{4},-\Large\frac{1}{4},\normalsize 1\Large\frac{1}{3},\normalsize -1\Large\frac{1}{3},\Large\frac{7}{2},-\Large\frac{7}{2}[/latex]

Ordering Fractions on the Number Line

In the following exercises, order each pair of numbers, using [latex]<[/latex] or [latex]>[/latex].

  1. [latex]-1\text{ ___}-\Large\frac{2}{5}[/latex]
  2. [latex]-2\Large\frac{1}{2}\normalsize\text{ ___}- 3[/latex]

Multiply and Divide Fractions

Simplify Fractions

In the following exercises, simplify.

  1. [latex]-\Large\frac{63}{84}[/latex]
  2. [latex]-\Large\frac{90}{120}[/latex]

  3. [latex]-\Large\frac{14a}{14b}[/latex]
  4. [latex]-\Large\frac{8x}{8y}[/latex]

Multiply Fractions

In the following exercises, multiply.

  1. [latex]\Large\frac{2}{5}\cdot\Large\frac{8}{13}[/latex]
  2. [latex]-\Large\frac{1}{3}\cdot\Large\frac{12}{7}[/latex]

  3. [latex]\Large\frac{2}{9}\cdot\Large\left(-\Large\frac{45}{32}\right)[/latex]
  4. [latex]6m\cdot\Large\frac{4}{11}[/latex]

  5. [latex]-\Large\frac{1}{4}\normalsize\left(-32\right)[/latex]
  6. [latex]3\Large\frac{1}{5}\normalsize\cdot 1\Large\frac{7}{8}[/latex]

Find Reciprocals

In the following exercises, find the reciprocal.

  1. [latex]\Large\frac{2}{9}[/latex]
  2. [latex]\Large\frac{15}{4}[/latex]

  3. [latex]3[/latex]
  4. [latex]-\Large\frac{1}{4}[/latex]

Exercise 5

Fill in the chart.

Opposite Absolute Value Reciprocal
[latex]-\Large\frac{5}{13}[/latex]
[latex]\Large\frac{3}{10}[/latex]
[latex]\Large\frac{9}{4}[/latex]
[latex]-12[/latex]

Divide Fractions

In the following exercises, divide.

  1. [latex]\Large\frac{2}{3}\div\Large\frac{1}{6}[/latex]

  2. [latex]\Large\left(-\frac{3x}{5}\right)\div\Large\left(-\frac{2y}{3}\right)[/latex]
  3. [latex]\Large\frac{4}{5}\normalsize\div 3[/latex]

  4. [latex]8\div 2\Large\frac{2}{3}[/latex]
  5. [latex]8\Large\frac{2}{3}\normalsize\div 1\Large\frac{1}{12}[/latex]

Multiply and Divide Mixed Numbers and Complex Fractions

In the following exercises, perform the indicated operation.

  1. [latex]3\Large\frac{1}{5}\normalsize\cdot 1\Large\frac{7}{8}[/latex]
  2. [latex]-5\Large\frac{7}{12}\normalsize\cdot 4\Large\frac{4}{11}[/latex]

  3. [latex]8\div 2\Large\frac{2}{3}[/latex]
  4. [latex]8\Large\frac{2}{3}\normalsize\div 1\Large\frac{1}{12}[/latex]

Translate Phrases to Expressions with Fractions

In the following exercises, translate the English phrase into an algebraic expression.

  1. the quotient of [latex]8[/latex] and [latex]y[/latex]
  2. the quotient of [latex]V[/latex] and the difference of [latex]h[/latex] and [latex]6[/latex]

Simplify Complex Fractions

In the following exercises, simplify the complex fraction

  1. [latex]\Large\frac{\LARGE\frac{5}{8}}{\LARGE\frac{4}{5}}[/latex]
  2. [latex]\Large\frac{\LARGE\frac{8}{9}}{-4}[/latex]

  3. [latex]\Large\frac{\LARGE\frac{n}{4}}{\LARGE\frac{3}{8}}[/latex]
  4. [latex]\Large\frac{\normalsize-1\LARGE\frac{5}{6}}{-\LARGE\frac{1}{12}}[/latex]

Simplify Fractions

In the following exercises, simplify.

  1. [latex]\Large\frac{5+16}{5}[/latex]
  2. [latex]\Large\frac{8\cdot 4-{5}^{2}}{3\cdot 12}[/latex]

  3. [latex]\Large\frac{8\cdot 7+5\left(8 - 10\right)}{9\cdot 3 - 6\cdot 4}[/latex]

Add and Subtract Fractions with Common Denominators

Add Fractions with a Common Denominator

In the following exercises, add.

  1. [latex]\Large\frac{3}{8}+\Large\frac{2}{8}[/latex]

  2. [latex]\Large\frac{4}{5}+\Large\frac{1}{5}[/latex]
  3. [latex]\Large\frac{2}{5}+\Large\frac{1}{5}[/latex]

  4. [latex]\Large\frac{15}{32}+\Large\frac{9}{32}[/latex]
  5. [latex]\Large\frac{x}{10}+\Large\frac{7}{10}[/latex]

Subtract Fractions with a Common Denominator

In the following exercises, subtract.

  1. [latex]\Large\frac{8}{11}-\Large\frac{6}{11}[/latex]
  2. [latex]\Large\frac{11}{12}-\Large\frac{5}{12}[/latex]

  3. [latex]\Large\frac{4}{5}-\frac{y}{5}[/latex]
  4. [latex]-\Large\frac{31}{30}-\Large\frac{7}{30}[/latex]

  5. [latex]\Large\frac{3}{2}-\Large\left(\frac{3}{2}\right)[/latex]
  6. [latex]\Large\frac{11}{15}-\Large\frac{5}{15}-\Large\left(-\frac{2}{15}\right)[/latex]

Add and Subtract Fractions with Different Denominators

Find the Least Common Denominator (LCD)

In the following exercises, find the least common denominator.

  1. [latex]\Large\frac{1}{3}\normalsize\text{ and }\Large\frac{1}{12}[/latex]
  2. [latex]\Large\frac{1}{3}\normalsize\text{ and }\Large\frac{4}{5}[/latex]

  3. [latex]\Large\frac{8}{15}\normalsize\text{ and }\Large\frac{11}{20}[/latex]
  4. [latex]\Large\frac{3}{4},\Large\frac{1}{6},\normalsize\text{ and }\Large\frac{5}{10}[/latex]

Convert Fractions to Equivalent Fractions with the LCD

In the following exercises, change to equivalent fractions using the given LCD.

  1. [latex]\Large\frac{1}{3}\normalsize\text{ and }\Large\frac{1}{5},\normalsize\text{LCD}=15[/latex]
  2. [latex]\Large\frac{3}{8}\normalsize\text{ and }\Large\frac{5}{6},\normalsize\text{LCD}=24[/latex]

  3. [latex]-\Large\frac{9}{16}\normalsize\text{ and }\Large\frac{5}{12},\normalsize\text{LCD}=48[/latex]
  4. [latex]\Large\frac{1}{3}\normalsize\text{,}\Large\frac{3}{4}\normalsize\text{ and }\Large\frac{4}{5},\normalsize\text{LCD}=60[/latex]

Identify and Use Fraction Operations

In the following exercises, perform the indicated operations and simplify.

  1. [latex]\Large\frac{1}{5}+\Large\frac{2}{3}[/latex]
  2. [latex]\Large\frac{11}{12}-\Large\frac{2}{3}[/latex]

  3. [latex]-\Large\frac{9}{10}-\Large\frac{3}{4}[/latex]
  4. [latex]-\Large\frac{11}{36}-\Large\frac{11}{20}[/latex]

  5. [latex]-\Large\frac{22}{25}+\Large\frac{9}{40}[/latex]
  6. [latex]\Large\frac{y}{10}-\Large\frac{1}{3}[/latex]

  7. [latex]\Large\frac{2}{5}+\Large\left(-\frac{5}{9}\right)[/latex]
  8. [latex]\Large\frac{4}{11}\div\Large\frac{2}{7d}[/latex]

  9. [latex]\Large\frac{2}{5}+\Large\left(-\frac{3n}{8}\right)\Large\left(-\frac{2}{9n}\right)[/latex]
  10. [latex]\Large\frac{{\left(\Large\frac{2}{3}\right)}^{2}}{{\Large\left(\frac{5}{8}\right)}^{2}}[/latex]

  11. [latex]\Large\left(\frac{11}{12}+\Large\frac{3}{8}\right)\div\Large\left(\Large\frac{5}{6}-\Large\frac{1}{10}\right)[/latex]

Mixed Practice

In the following exercises, evaluate.

Exercise 1

[latex]y-\Large\frac{4}{5}[/latex] when

  1. [latex]y=-\Large\frac{4}{5}[/latex]
  2. [latex]y=\Large\frac{1}{4}[/latex]

Exercise 2

[latex]6m{n}^{2}[/latex] when [latex]m=\Large\frac{3}{4}\normalsize\text{ and }n=-\Large\frac{1}{3}[/latex]

Add and Subtract Mixed Numbers

In the following exercises, perform the indicated operation.

  1. [latex]4\Large\frac{1}{3}\normalsize+9\Large\frac{1}{3}[/latex]

  2. [latex]6\Large\frac{2}{5}\normalsize+7\Large\frac{3}{5}[/latex]
  3. [latex]5\Large\frac{8}{11}\normalsize+2\Large\frac{4}{11}[/latex]

  4. [latex]3\Large\frac{5}{8}\normalsize+3\Large\frac{7}{8}[/latex]
  5. [latex]9\Large\frac{13}{20}\normalsize-4\Large\frac{11}{20}[/latex]

  6. [latex]2\Large\frac{3}{10}\normalsize-1\Large\frac{9}{10}[/latex]
  7. [latex]2\Large\frac{11}{12}\normalsize-1\Large\frac{7}{12}[/latex]

  8. [latex]8\Large\frac{6}{11}\normalsize-2\Large\frac{9}{11}[/latex]

Solve Equations with Fractions

Determine Whether a Fraction is a Solution of an Equation

In the following exercises, determine whether the each number is a solution of the given equation.

Exercise 1

[latex]x-\Large\frac{1}{2}=\Large\frac{1}{6}\normalsize\text{:}[/latex]

  1. [latex]x=1[/latex]
  2. [latex]x=\Large\frac{2}{3}[/latex]
  3. [latex]x=-\Large\frac{1}{3}[/latex]

Exercise 2

[latex]y+\Large\frac{3}{5}=\Large\frac{5}{9}\normalsize\text{:}[/latex]

  1. [latex]y=\Large\frac{1}{2}[/latex]
  2. [latex]y=\Large\frac{52}{45}[/latex]
  3. [latex]y=-\Large\frac{2}{45}[/latex]

Solve Equations with Fractions using the Addition, Subtraction, and Division Properties of Equality

In the following exercises, solve the equation.

  1. [latex]n+\Large\frac{9}{11}=\Large\frac{4}{11}[/latex]

  2. [latex]x-\Large\frac{1}{6}=\Large\frac{7}{6}[/latex]
  3. [latex]h-\Large\left(-\frac{7}{8}\right)=-\Large\frac{2}{5}[/latex]

  4. [latex]\Large\frac{x}{5}\normalsize=-10[/latex]
  5. [latex]-z=23[/latex]

Translate Sentences to Equations and Solve

In the following exercises, translate and solve.

  1. The sum of two-thirds and [latex]n[/latex] is [latex]-\Large\frac{3}{5}[/latex].
  2. The difference of [latex]q[/latex] and one-tenth is [latex]\Large\frac{1}{2}[/latex].

  3. The quotient of [latex]p[/latex] and [latex]-4[/latex] is [latex]-8[/latex].
  4. Three-eighths of [latex]y[/latex] is [latex]24[/latex].

Chapter Practice Test

Convert the improper fraction to a mixed number.

  1. [latex]\Large\frac{19}{5}[/latex]

Convert the mixed number to an improper fraction.

  1. [latex]3\Large\frac{2}{7}[/latex]

Locate the numbers on a number line.

  1. [latex]\Large\frac{1}{2}\normalsize ,1\Large\frac{2}{3}\normalsize ,-2\Large\frac{3}{4}\normalsize ,\text{ and }\Large\frac{9}{4}[/latex]

In the following exercises, simplify.

  1. [latex]\Large\frac{5}{20}[/latex]

  2. [latex]\Large\frac{18r}{27s}[/latex]
  3. [latex]\Large\frac{1}{3}\cdot\Large\frac{3}{4}[/latex]

  4. [latex]\Large\frac{3}{5}\normalsize\cdot 15[/latex]
  5. [latex]-36u\Large\left(-\frac{4}{9}\right)[/latex]

  6. [latex]-5\Large\frac{7}{12}\normalsize\cdot 4\Large\frac{4}{11}[/latex]
  7. [latex]-\Large\frac{5}{6}\div\Large\frac{5}{12}[/latex]

  8. [latex]\Large\frac{7}{11}\div\Large\left(-\frac{7}{11}\right)[/latex]
  9. [latex]\Large\frac{9a}{10}\div\Large\frac{15a}{8}[/latex]

  10. [latex]-6\Large\frac{2}{5}\normalsize\div 4[/latex]
  11. [latex]\left(-15\Large\frac{5}{6}\right)\normalsize\div\left(-3\Large\frac{1}{6}\right)[/latex]

  12. [latex]\Large\frac{-6}{\LARGE\frac{6}{11}}[/latex]
  13. [latex]\Large\frac{\LARGE\frac{p}{2}}{\LARGE\frac{q}{5}}[/latex]

  14. [latex]\Large\frac{-\LARGE\frac{4}{15}}{-2\LARGE\frac{2}{3}}[/latex]
  15. [latex]\Large\frac{{9}^{2}-{4}^{2}}{9 - 4}[/latex]

  16. [latex]\Large\frac{2}{d}+\Large\frac{9}{d}[/latex]
  17. [latex]-\Large\frac{3}{13}+\Large\left(-\frac{4}{13}\right)[/latex]

  18. [latex]-\Large\frac{22}{25}+\Large\frac{9}{40}[/latex]
  19. [latex]\Large\frac{2}{5}+\Large\left(-\frac{7}{5}\right)[/latex]

  20. [latex]-\Large\frac{3}{10}+\Large\left(-\frac{5}{8}\right)[/latex]
  21. [latex]-\Large\frac{3}{4}\div\Large\frac{x}{3}[/latex]

  22. [latex]\Large\frac{{2}^{3}-{2}^{2}}{{\LARGE\left(\frac{3}{4}\right)}^{2}}[/latex]
  23. [latex]\Large\frac{\LARGE\frac{5}{14}+\LARGE\frac{1}{8}}{\LARGE\frac{9}{56}}[/latex]

Evaluate [latex]x+\Large\frac{1}{3}[/latex] when

  1. [latex]x=\Large\frac{2}{3}[/latex]
  2. [latex]x=-\Large\frac{5}{6}[/latex]

In the following exercises, solve the equation.

  1. [latex]y+\Large\frac{3}{5}=\Large\frac{7}{5}[/latex]

  2. [latex]a-\Large\frac{3}{10}=-\Large\frac{9}{10}[/latex]
  3. [latex]f+\Large\left(-\frac{2}{3}\right)=\Large\frac{5}{12}[/latex]

  4. [latex]\Large\frac{m}{-2}\normalsize=-16[/latex]
  5. [latex]-\Large\frac{2}{3}\normalsize c=18[/latex]

Translate and solve: The quotient of [latex]p[/latex] and [latex]-4[/latex] is [latex]-8[/latex]. Solve for [latex][/latex]p[/late