Practice Makes Perfect

Identify Polynomials, Monomials, Binomials and Trinomials
In the following exercises, determine if each of the polynomials is a monomial, binomial, trinomial, or other polynomial.

[latex]5x+2[/latex]

binomial

[latex]{z}^{2}-5z - 6[/latex]

[latex]{a}^{2}+9a+18[/latex]

trinomial

[latex]-12{p}^{4}[/latex]

[latex]{y}^{3}-8{y}^{2}+2y - 16[/latex]

polynomial

[latex]10 - 9x[/latex]

[latex]23{y}^{2}[/latex]

monomial

[latex]{m}^{4}+4{m}^{3}+6{m}^{2}+4m+1[/latex]

Determine the Degree of Polynomials
In the following exercises, determine the degree of each polynomial.

[latex]8{a}^{5}-2{a}^{3}+1[/latex]

5

[latex]5{c}^{3}+11{c}^{2}-c - 8[/latex]

[latex]3x - 12[/latex]

1

[latex]4y+17[/latex]

[latex]-13[/latex]

0

[latex]-22[/latex]

Add and Subtract Monomials
In the following exercises, add or subtract the monomials.

[latex]{\text{6x}}^{2}+9{x}^{2}[/latex]

15x²

[latex]{\text{4y}}^{3}+6{y}^{3}[/latex]

[latex]-12u+4u[/latex]

−8u

[latex]-3m+9m[/latex]

[latex]5a+7b[/latex]

5a + 7b

[latex]8y+6z[/latex]

Add: [latex]\text{}4a,-3b,-8a[/latex]

−4a −3b

Add: [latex]4x,3y,-3x[/latex]

[latex]18x - 2x[/latex]

16x

[latex]13a - 3a[/latex]

Subtract [latex]5{x}^{6}\text{from}-12{x}^{6}[/latex]

−17x⁶

Subtract [latex]2{p}^{4}\text{from}-7{p}^{4}[/latex]

Add and Subtract Polynomials
In the following exercises, add or subtract the polynomials.

[latex]\left(4{y}^{2}+10y+3\right)+\left(8{y}^{2}-6y+5\right)[/latex]

12y² + 4y + 8

[latex]\left(7{x}^{2}-9x+2\right)+\left(6{x}^{2}-4x+3\right)[/latex]

[latex]\left({x}^{2}+6x+8\right)+\left(-4{x}^{2}+11x - 9\right)[/latex]

−3x² + 17x − 1

[latex]\left({y}^{2}+9y+4\right)+\left(-2{y}^{2}-5y - 1\right)[/latex]

[latex]\left(3{a}^{2}+7\right)+\left({a}^{2}-7a - 18\right)[/latex]

4a² − 7a − 11

[latex]\left({p}^{2}-5p - 11\right)+\left(3{p}^{2}+9\right)[/latex]

[latex]\left(6{m}^{2}-9m - 3\right)-\left(2{m}^{2}+m - 5\right)[/latex]

4m² − 10m + 2

[latex]\left(3{n}^{2}-4n+1\right)-\left(4{n}^{2}-n - 2\right)[/latex]

[latex]\left({z}^{2}+8z+9\right)-\left({z}^{2}-3z+1\right)[/latex]

11z + 8

[latex]\left({z}^{2}-7z+5\right)-\left({z}^{2}-8z+6\right)[/latex]

[latex]\left(12{s}^{2}-15s\right)-\left(s - 9\right)[/latex]

12s² − 16s + 9

[latex]\left(10{r}^{2}-20r\right)-\left(r - 8\right)[/latex]

Find the sum of [latex]\left(2{p}^{3}-8\right)[/latex] and [latex]\left({p}^{2}+9p+18\right)[/latex]

2p³ + p² + 9p + 10

Find the sum of [latex]\left({q}^{2}+4q+13\right)[/latex] and [latex]\left(7{q}^{3}-3\right)[/latex]

Subtract [latex]\left(7{x}^{2}-4x+2\right)[/latex] from [latex]\left(8{x}^{2}-x+6\right)[/latex]

x² + 3x + 4

Subtract [latex]\left(5{x}^{2}-x+12\right)[/latex] from [latex]\left(9{x}^{2}-6x - 20\right)[/latex]

Find the difference of [latex]\left({w}^{2}+w - 42\right)[/latex] and [latex]\left({w}^{2}-10w+24\right)[/latex]

11w − 66

Find the difference of [latex]\left({z}^{2}-3z - 18\right)[/latex] and [latex]\left({z}^{2}+5z - 20\right)[/latex]

Evaluate a Polynomial for a Given Value
In the following exercises, evaluate each polynomial for the given value.

[latex]\text{Evaluate}8{y}^{2}-3y+2[/latex]

ⓐ [latex]y=5[/latex]
ⓑ [latex]y=-2[/latex]
ⓒ [latex]y=0[/latex]

ⓐ 187
ⓑ 40
ⓒ 2

[latex]\text{Evaluate}5{y}^{2}-y - 7\text{when:}[/latex]

ⓐ [latex]y=-4[/latex]
ⓑ [latex]y=1[/latex]
ⓒ [latex]y=0[/latex]

[latex]\text{Evaluate}4 - 36x\text{when:}[/latex]

ⓐ [latex]x=3[/latex]
ⓑ [latex]x=0[/latex]
ⓒ [latex]x=-1[/latex]

ⓐ −104
ⓑ 4
ⓒ 40

[latex]\text{Evaluate}16 - 36{x}^{2}\text{when:}[/latex]

ⓐ [latex]x=-1[/latex]
ⓑ [latex]x=0[/latex]
ⓒ [latex]x=2[/latex]

A window washer drops a squeegee from a platform [latex]275[/latex] feet high. The polynomial [latex]-16{t}^{2}+275[/latex] gives the height of the squeegee [latex]t[/latex] seconds after it was dropped. Find the height after [latex]t=4[/latex] seconds.

19 feet

A manufacturer of microwave ovens has found that the revenue received from selling microwaves at a cost of p dollars each is given by the polynomial [latex]-5{p}^{2}+350p[/latex]. Find the revenue received when [latex]p=50[/latex] dollars.

Everyday Math

Fuel Efficiency The fuel efficiency (in miles per gallon) of a bus going at a speed of [latex]x[/latex] miles per hour is given by the polynomial [latex]-\Large\frac{1}{160}\normalsize{x}^{2}+\Large\frac{1}{2}\normalsize x[/latex]. Find the fuel efficiency when [latex]x=40\text{mph.}[/latex]

10 mpg

Stopping Distance The number of feet it takes for a car traveling at [latex]x[/latex] miles per hour to stop on dry, level concrete is given by the polynomial [latex]0.06{x}^{2}+1.1x[/latex]. Find the stopping distance when [latex]x=60\text{mph.}[/latex]

Writing Exercises

Using your own words, explain the difference between a monomial, a binomial, and a trinomial.

Answers will vary.

Eloise thinks the sum [latex]5{x}^{2}+3{x}^{4}[/latex] is [latex]8{x}^{6}[/latex]. What is wrong with her reasoning?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Practice Makes Perfect

Simplify Expressions with Exponents
In the following exercises, simplify each expression with exponents.

[latex]{4}^{5}[/latex]

1,024

[latex]{10}^{3}[/latex]

[latex]{\left(\Large\frac{1}{2}\normalsize\right)}^{2}[/latex]

[latex]\Large\frac{1}{4}[/latex]

[latex]{\left(\Large\frac{3}{5}\normalsize\right)}^{2}[/latex]

[latex]{\left(0.2\right)}^{3}[/latex]

0.008

[latex]{\left(0.4\right)}^{3}[/latex]

[latex]{\left(-5\right)}^{4}[/latex]

625

[latex]{\left(-3\right)}^{5}[/latex]

[latex]{-5}^{4}[/latex]

−625

[latex]{-3}^{5}[/latex]

[latex]{-10}^{4}[/latex]

−10,000

[latex]{-2}^{6}[/latex]

[latex]{\left(-\Large\frac{2}{3}\normalsize\right)}^{3}[/latex]

[latex]-\Large\frac{8}{27}[/latex]

[latex]{\left(-\Large\frac{1}{4}\normalsize\right)}^{4}[/latex]

[latex]-{0.5}^{2}[/latex]

−.25

[latex]-{0.1}^{4}[/latex]

Simplify Expressions Using the Product Property of Exponents
In the following exercises, simplify each expression using the Product Property of Exponents.

[latex]{x}^{3}\cdot {x}^{6}[/latex]

x⁹

[latex]{m}^{4}\cdot {m}^{2}[/latex]

[latex]a\cdot {a}^{4}[/latex]

a⁵

[latex]{y}^{12}\cdot y[/latex]

[latex]{3}^{5}\cdot {3}^{9}[/latex]

3¹⁴

[latex]{5}^{10}\cdot {5}^{6}[/latex]

[latex]z\cdot {z}^{2}\cdot {z}^{3}[/latex]

z⁶

[latex]a\cdot {a}^{3}\cdot {a}^{5}[/latex]

[latex]{x}^{a}\cdot {x}^{2}[/latex]

x^a+2

[latex]{y}^{p}\cdot {y}^{3}[/latex]

[latex]{y}^{a}\cdot {y}^{b}[/latex]

y^a+b

[latex]{x}^{p}\cdot {x}^{q}[/latex]

Simplify Expressions Using the Power Property of Exponents
In the following exercises, simplify each expression using the Power Property of Exponents.

[latex]{\left({u}^{4}\right)}^{2}[/latex]

u⁸

[latex]{\left({x}^{2}\right)}^{7}[/latex]

[latex]{\left({y}^{5}\right)}^{4}[/latex]

y²⁰

[latex]{\left({a}^{3}\right)}^{2}[/latex]

[latex]{\left({10}^{2}\right)}^{6}[/latex]

10¹²

[latex]{\left({2}^{8}\right)}^{3}[/latex]

[latex]{\left({x}^{15}\right)}^{6}[/latex]

x⁹⁰

[latex]{\left({y}^{12}\right)}^{8}[/latex]

[latex]{\left({x}^{2}\right)}^{y}[/latex]

x^2y

[latex]{\left({y}^{3}\right)}^{x}[/latex]

[latex]{\left({5}^{x}\right)}^{y}[/latex]

5^xy

[latex]{\left({7}^{a}\right)}^{b}[/latex]

Simplify Expressions Using the Product to a Power Property
In the following exercises, simplify each expression using the Product to a Power Property.

[latex]{\left(5a\right)}^{2}[/latex]

25a²

[latex]{\left(7x\right)}^{2}[/latex]

[latex]{\left(-6m\right)}^{3}[/latex]

−216m³

[latex]{\left(-9n\right)}^{3}[/latex]

[latex]{\left(4rs\right)}^{2}[/latex]

16r²s²

[latex]{\left(5ab\right)}^{3}[/latex]

[latex]{\left(4xyz\right)}^{4}[/latex]

256x⁴y⁴z⁴

[latex]{\left(-5abc\right)}^{3}[/latex]

Simplify Expressions by Applying Several Properties
In the following exercises, simplify each expression.

[latex]{\left({x}^{2}\right)}^{4}\cdot {\left({x}^{3}\right)}^{2}[/latex]

x¹⁴

[latex]{\left({y}^{4}\right)}^{3}\cdot {\left({y}^{5}\right)}^{2}[/latex]

[latex]{\left({a}^{2}\right)}^{6}\cdot {\left({a}^{3}\right)}^{8}[/latex]

a³⁶

[latex]{\left({b}^{7}\right)}^{5}\cdot {\left({b}^{2}\right)}^{6}[/latex]

[latex]{\left(3x\right)}^{2}\left(5x\right)[/latex]

45x³

[latex]{\left(2y\right)}^{3}\left(6y\right)[/latex]

[latex]{\left(5a\right)}^{2}{\left(2a\right)}^{3}[/latex]

200a⁵

[latex]{\left(4b\right)}^{2}{\left(3b\right)}^{3}[/latex]

[latex]{\left(2{m}^{6}\right)}^{3}[/latex]

8m¹⁸

[latex]{\left(3{y}^{2}\right)}^{4}[/latex]

[latex]{\left(10{x}^{2}y\right)}^{3}[/latex]

1,000x⁶y³

[latex]{\left(2m{n}^{4}\right)}^{5}[/latex]

[latex]{\left(-2{a}^{3}{b}^{2}\right)}^{4}[/latex]

16a¹²b⁸

[latex]{\left(-10{u}^{2}{v}^{4}\right)}^{3}[/latex]

[latex]{\left(\Large\frac{2}{3}\normalsize{x}^{2}y\right)}^{3}[/latex]

[latex]\Large\frac{8}{27}\normalsize{x}^{6}{y}^{3}[/latex]

[latex]{\left(\Large\frac{7}{9}\normalsize p{q}^{4}\right)}^{2}[/latex]

[latex]{\left(8{a}^{3}\right)}^{2}{\left(2a\right)}^{4}[/latex]

1,024a¹⁰

[latex]{\left(5{r}^{2}\right)}^{3}{\left(3r\right)}^{2}[/latex]

[latex]{\left(10{p}^{4}\right)}^{3}{\left(5{p}^{6}\right)}^{2}[/latex]

25,000p²⁴

[latex]{\left(4{x}^{3}\right)}^{3}{\left(2{x}^{5}\right)}^{4}[/latex]

[latex]{\left(\Large\frac{1}{2}\normalsize{x}^{2}{y}^{3}\right)}^{4}{\left(4{x}^{5}{y}^{3}\right)}^{2}[/latex]

x¹⁸y¹⁸

[latex]{\left(\Large\frac{1}{3}\normalsize{m}^{3}{n}^{2}\right)}^{4}{\left(9{m}^{8}{n}^{3}\right)}^{2}[/latex]

[latex]{\left(3{m}^{2}n\right)}^{2}{\left(2m{n}^{5}\right)}^{4}[/latex]

144m⁸n²²

[latex]{\left(2p{q}^{4}\right)}^{3}{\left(5{p}^{6}q\right)}^{2}[/latex]

Multiply Monomials
In the following exercises, multiply the following monomials.

[latex]\left(12{x}^{2}\right)\left(-5{x}^{4}\right)[/latex]

−60x⁶

[latex]\left(-10{y}^{3}\right)\left(7{y}^{2}\right)[/latex]

[latex]\left(-8{u}^{6}\right)\left(-9u\right)[/latex]

72u⁷

[latex]\left(-6{c}^{4}\right)\left(-12c\right)[/latex]

[latex]\left(\Large\frac{1}{5}\normalsize{r}^{8}\right)\left(20{r}^{3}\right)[/latex]

4r¹¹

[latex]\left(\Large\frac{1}{4}\normalsize{a}^{5}\right)\left(36{a}^{2}\right)[/latex]

[latex]\left(4{a}^{3}b\right)\left(9{a}^{2}{b}^{6}\right)[/latex]

36a⁵b⁷

[latex]\left(6{m}^{4}{n}^{3}\right)\left(7m{n}^{5}\right)[/latex]

[latex]\left(\Large\frac{4}{7}\normalsize x{y}^{2}\right)\left(14x{y}^{3}\right)[/latex]

8x²y⁵

[latex]\left(\Large\frac{5}{8}\normalsize{u}^{3}v\right)\left(24{u}^{5}v\right)[/latex]

[latex]\left(\Large\frac{2}{3}\normalsize{x}^{2}y\right)\left(\Large\frac{3}{4}\normalsize x{y}^{2}\right)[/latex]

[latex]\Large\frac{1}{2}\normalsize{x}^{3}{y}^{3}[/latex]

[latex]\left(\Large\frac{3}{5}\normalsize{m}^{3}{n}^{2}\right)\left(\Large\frac{5}{9}\normalsize{m}^{2}{n}^{3}\right)[/latex]

Everyday Math

Email Janet emails a joke to six of her friends and tells them to forward it to six of their friends, who forward it to six of their friends, and so on. The number of people who receive the email on the second round is [latex]{6}^{2}[/latex], on the third round is [latex]{6}^{3}[/latex], as shown in the table. How many people will receive the email on the eighth round? Simplify the expression to show the number of people who receive the email.

Round	Number of people
[latex]1[/latex]	[latex]6[/latex]
[latex]2[/latex]	[latex]{6}^{2}[/latex]
[latex]3[/latex]	[latex]{6}^{3}[/latex]
[latex]\dots [/latex]	[latex]\dots [/latex]
[latex]8[/latex]	[latex]?[/latex]

1,679,616

Salary Raul’s boss gives him a [latex]\text{5%}[/latex] raise every year on his birthday. This means that each year, Raul’s salary is [latex]1.05[/latex] times his last year’s salary. If his original salary was [latex]{$40,000}[/latex] , his salary after [latex]1[/latex] year was [latex]{$40,000}\left(1.05\right)[/latex], after [latex]2[/latex] years was [latex]{$40,000}{\left(1.05\right)}^{2}[/latex], after [latex]3[/latex] years was [latex]{$40,000}{\left(1.05\right)}^{3}[/latex], as shown in the table below. What will Raul’s salary be after [latex]10[/latex] years? Simplify the expression, to show Raul’s salary in dollars.

Year	Salary
[latex]1[/latex]	[latex]{$40,000}\left(1.05\right)[/latex]
[latex]2[/latex]	[latex]{$40,000}{\left(1.05\right)}^{2}[/latex]
[latex]3[/latex]	[latex]{$40,000}{\left(1.05\right)}^{3}[/latex]
[latex]\dots [/latex]	[latex]\dots [/latex]
[latex]10[/latex]	[latex]?[/latex]

Writing Exercises

Use the Product Property for Exponents to explain why [latex]x\cdot x={x}^{2}[/latex].

Answers will vary.

Explain why [latex]{-5}^{3}={\left(-5\right)}^{3}[/latex] but [latex]{-5}^{4}\ne {\left(-5\right)}^{4}[/latex].

Jorge thinks [latex]{\left(\Large\frac{1}{2}\normalsize\right)}^{2}[/latex] is [latex]1[/latex]. What is wrong with his reasoning?

Answers will vary.

Explain why [latex]{x}^{3}\cdot {x}^{5}[/latex] is [latex]{x}^{8}[/latex], and not [latex]{x}^{15}[/latex].

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

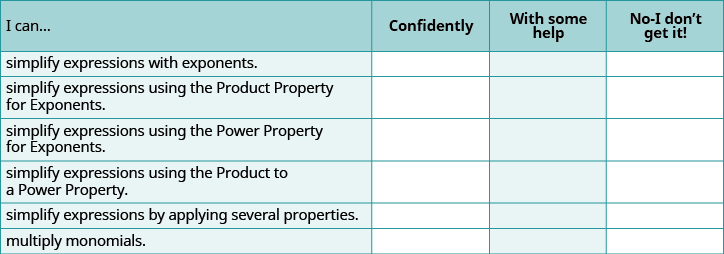
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

 

Practice Makes Perfect

Multiply a Polynomial by a Monomial
In the following exercises, multiply.

[latex]4\left(x+10\right)[/latex]

4x + 40

[latex]6\left(y+8\right)[/latex]

[latex]15\left(r - 24\right)[/latex]

15r − 360

[latex]12\left(v - 30\right)[/latex]

[latex]-3\left(m+11\right)[/latex]

−3m − 33

[latex]-4\left(p+15\right)[/latex]

[latex]-8\left(z - 5\right)[/latex]

−8z + 40

[latex]-3\left(x - 9\right)[/latex]

[latex]u\left(u+5\right)[/latex]

u² + 5u

[latex]q\left(q+7\right)[/latex]

[latex]n\left({n}^{2}-3n\right)[/latex]

n³ − 3n²

[latex]s\left({s}^{2}-6s\right)[/latex]

[latex]12x\left(x - 10\right)[/latex]

12x² − 120x

[latex]9m\left(m - 11\right)[/latex]

[latex]-9a\left(3a+5\right)[/latex]

−27a² − 45a

[latex]-4p\left(2p+7\right)[/latex]

[latex]6x\left(4x+y\right)[/latex]

24x² + 6xy

[latex]5a\left(9a+b\right)[/latex]

[latex]5p\left(11p - 5q\right)[/latex]

55p² − 25pq

[latex]12u\left(3u - 4v\right)[/latex]

[latex]3\left({v}^{2}+10v+25\right)[/latex]

3v² + 30v + 75

[latex]6\left({x}^{2}+8x+16\right)[/latex]

[latex]2n\left(4{n}^{2}-4n+1\right)[/latex]

8n³ − 8n² + 2n

[latex]3r\left(2{r}^{2}-6r+2\right)[/latex]

[latex]-8y\left({y}^{2}+2y - 15\right)[/latex]

−8y³ − 16y² + 120y

[latex]-5m\left({m}^{2}+3m - 18\right)[/latex]

[latex]5{q}^{3}\left({q}^{2}-2q+6\right)[/latex]

5q⁵ − 10q⁴ + 30q³

[latex]9{r}^{3}\left({r}^{2}-3r+5\right)[/latex]

[latex]-4{z}^{2}\left(3{z}^{2}+12z - 1\right)[/latex]

−12z⁴ − 48z³ + 4z²

[latex]-3{x}^{2}\left(7{x}^{2}+10x - 1\right)[/latex]

[latex]\left(2y - 9\right)y[/latex]

2y² − 9y

[latex]\left(8b - 1\right)b[/latex]

[latex]\left(w - 6\right)\cdot 8[/latex]

8w − 48

[latex]\left(k - 4\right)\cdot 5[/latex]

Multiply a Binomial by a Binomial
In the following exercises, multiply the following binomials using: ⓐ the Distributive Property ⓑ the FOIL method ⓒ the Vertical method

[latex]\left(x+4\right)\left(x+6\right)[/latex]

x² + 10x + 24

[latex]\left(u+8\right)\left(u+2\right)[/latex]

[latex]\left(n+12\right)\left(n - 3\right)[/latex]

n² + 9n − 36

[latex]\left(y+3\right)\left(y - 9\right)[/latex]

In the following exercises, multiply the following binomials. Use any method.

[latex]\left(y+8\right)\left(y+3\right)[/latex]

y² + 11y + 24

[latex]\left(x+5\right)\left(x+9\right)[/latex]

[latex]\left(a+6\right)\left(a+16\right)[/latex]

a² + 22a + 96

[latex]\left(q+8\right)\left(q+12\right)[/latex]

[latex]\left(u - 5\right)\left(u - 9\right)[/latex]

u² − 14u + 45

[latex]\left(r - 6\right)\left(r - 2\right)[/latex]

[latex]\left(z - 10\right)\left(z - 22\right)[/latex]

z² − 32z + 220

[latex]\left(b - 5\right)\left(b - 24\right)[/latex]

[latex]\left(x - 4\right)\left(x+7\right)[/latex]

x² + 3x − 28

[latex]\left(s - 3\right)\left(s+8\right)[/latex]

[latex]\left(v+12\right)\left(v - 5\right)[/latex]

v² + 7v − 60

[latex]\left(d+15\right)\left(d - 4\right)[/latex]

[latex]\left(6n+5\right)\left(n+1\right)[/latex]

6n² + 11n + 5

[latex]\left(7y+1\right)\left(y+3\right)[/latex]

[latex]\left(2m - 9\right)\left(10m+1\right)[/latex]

20m² − 88m − 9

[latex]\left(5r - 4\right)\left(12r+1\right)[/latex]

[latex]\left(4c - 1\right)\left(4c+1\right)[/latex]

16c² − 1

[latex]\left(8n - 1\right)\left(8n+1\right)[/latex]

[latex]\left(3u - 8\right)\left(5u - 14\right)[/latex]

15u² − 82u + 112

[latex]\left(2q - 5\right)\left(7q - 11\right)[/latex]

[latex]\left(a+b\right)\left(2a+3b\right)[/latex]

2a² + 5ab + 3b²

[latex]\left(r+s\right)\left(3r+2s\right)[/latex]

[latex]\left(5x-y\right)\left(x - 4\right)[/latex]

5x² − 20x − xy + 4y

[latex]\left(4z-y\right)\left(z - 6\right)[/latex]

Multiply a Trinomial by a Binomial
In the following exercises, multiply using ⓐ the Distributive Property and ⓑ the Vertical Method.

[latex]\left(u+4\right)\left({u}^{2}+3u+2\right)[/latex]

u³ + 7u² + 14u + 8

[latex]\left(x+5\right)\left({x}^{2}+8x+3\right)[/latex]

[latex]\left(a+10\right)\left(3{a}^{2}+a - 5\right)[/latex]

3a³ + 31a² + 5a − 50

[latex]\left(n+8\right)\left(4{n}^{2}+n - 7\right)[/latex]

In the following exercises, multiply. Use either method.

[latex]\left(y - 6\right)\left({y}^{2}-10y+9\right)[/latex]

y³ − 16y² + 69y − 54

[latex]\left(k - 3\right)\left({k}^{2}-8k+7\right)[/latex]

[latex]\left(2x+1\right)\left({x}^{2}-5x - 6\right)[/latex]

2x³ − 9x² − 17x − 6

[latex]\left(5v+1\right)\left({v}^{2}-6v - 10\right)[/latex]

Everyday Math

Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply [latex]13[/latex] times [latex]15[/latex]. Think of [latex]13[/latex] as [latex]10+3[/latex] and [latex]15[/latex] as [latex]10+5[/latex].

1. ⓐ Multiply [latex]\left(10+3\right)\left(10+5\right)[/latex] by the FOIL method.
2. ⓑ Multiply [latex]13\cdot 15[/latex] without using a calculator.
3. ⓒ Which way is easier for you? Why?

1. ⓐ 195
2. ⓑ 195
3. ⓐ Answers will vary.

Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply [latex]18[/latex] times [latex]17[/latex]. Think of [latex]18[/latex] as [latex]20 - 2[/latex] and [latex]17[/latex] as [latex]20 - 3[/latex].

1. ⓐ Multiply [latex]\left(20 - 2\right)\left(20 - 3\right)[/latex] by the FOIL method.
2. ⓑ Multiply [latex]18\cdot 17[/latex] without using a calculator.
3. ⓒ Which way is easier for you? Why?

Writing Exercises

Which method do you prefer to use when multiplying two binomials—the Distributive Property, the FOIL method, or the Vertical Method? Why?

Answers will vary.

Which method do you prefer to use when multiplying a trinomial by a binomial—the Distributive Property or the Vertical Method? Why?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Practice Makes Perfect

Simplify Expressions Using the Quotient Property of Exponents
In the following exercises, simplify.

[latex]\Large\frac{{4}^{8}}{{4}^{2}}[/latex]

4⁶

[latex]\Large\frac{{3}^{12}}{{3}^{4}}[/latex]

[latex]\Large\frac{{x}^{12}}{{x}^{3}}[/latex]

x⁹

[latex]\Large\frac{{u}^{9}}{{u}^{3}}[/latex]

[latex]\Large\frac{{r}^{5}}{r}[/latex]

r⁴

[latex]\Large\frac{{y}^{4}}{y}[/latex]

[latex]\Large\frac{{y}^{4}}{{y}^{20}}[/latex]

[latex]\Large\frac{1}{{y}^{16}}[/latex]

[latex]\Large\frac{{x}^{10}}{{x}^{30}}[/latex]

[latex]\Large\frac{{10}^{3}}{{10}^{15}}[/latex]

[latex]\Large\frac{1}{{10}^{12}}[/latex]

[latex]\Large\frac{{r}^{2}}{{r}^{8}}[/latex]

[latex]\Large\frac{a}{{a}^{9}}[/latex]

[latex]\Large\frac{1}{{a}^{8}}[/latex]

[latex]\Large\frac{2}{{2}^{5}}[/latex]

Simplify Expressions with Zero Exponents
In the following exercises, simplify.

[latex]{5}^{0}[/latex]

1

[latex]{10}^{0}[/latex]

[latex]{a}^{0}[/latex]

1

[latex]{x}^{0}[/latex]

[latex]-{7}^{0}[/latex]

−1

[latex]-{4}^{0}[/latex]

ⓐ [latex]{\left(10p\right)}^{0}[/latex]
ⓑ [latex]10{p}^{0}[/latex]

ⓐ 1
ⓑ 10

ⓐ [latex]{\left(3a\right)}^{0}[/latex]
ⓑ [latex]3{a}^{0}[/latex]

ⓐ [latex]{\left(-27{x}^{5}y\right)}^{0}[/latex]
ⓑ [latex]-27{x}^{5}{y}^{0}[/latex]

ⓐ 1
ⓑ −27x⁵

ⓐ [latex]{\left(-92{y}^{8}z\right)}^{0}[/latex]
ⓑ [latex]-92{y}^{8}{z}^{0}[/latex]

ⓐ [latex]{15}^{0}[/latex]
ⓑ [latex]{15}^{1}[/latex]

ⓐ 1
ⓑ 15

ⓐ [latex]-{6}^{0}[/latex]
ⓑ [latex]-{6}^{1}[/latex]

[latex]2\cdot {x}^{0}+5\cdot {y}^{0}[/latex]

7

[latex]8\cdot {m}^{0}-4\cdot {n}^{0}[/latex]

Simplify Expressions Using the Quotient to a Power Property
In the following exercises, simplify.

[latex]{\left(\Large\frac{3}{2}\normalsize\right)}^{5}[/latex]

[latex]\Large\frac{243}{32}[/latex]

[latex]{\left(\Large\frac{4}{5}\normalsize\right)}^{3}[/latex]

[latex]{\left(\Large\frac{m}{6}\normalsize\right)}^{3}[/latex]

[latex]\Large\frac{{m}^{3}}{216}[/latex]

[latex]{\left(\Large\frac{p}{2}\normalsize\right)}^{5}[/latex]

[latex]{\left(\Large\frac{x}{y}\normalsize\right)}^{10}[/latex]

[latex]\Large\frac{{x}^{10}}{{y}^{10}}[/latex]

[latex]{\left(\Large\frac{a}{b}\normalsize\right)}^{8}[/latex]

[latex]{\left(\Large\frac{a}{3b}\normalsize\right)}^{2}[/latex]

[latex]\Large\frac{{a}^{2}}{9{b}^{2}}[/latex]

[latex]{\left(\Large\frac{2x}{y}\normalsize\right)}^{4}[/latex]

Simplify Expressions by Applying Several Properties
In the following exercises, simplify.

[latex]\Large\frac{{\left({x}^{2}\right)}^{4}}{{x}^{5}}[/latex]

x³

[latex]\Large\frac{{\left({y}^{4}\right)}^{3}}{{y}^{7}}[/latex]

[latex]\Large\frac{{\left({u}^{3}\right)}^{4}}{{u}^{10}}[/latex]

u²

[latex]\Large\frac{{\left({y}^{2}\right)}^{5}}{{y}^{6}}[/latex]

[latex]\Large\frac{{y}^{8}}{{\left({y}^{5}\right)}^{2}}[/latex]

[latex]\Large\frac{1}{{y}^{2}}[/latex]

[latex]\Large\frac{{p}^{11}}{{\left({p}^{5}\right)}^{3}}[/latex]

[latex]\Large\frac{{r}^{5}}{{r}^{4}\cdot r}[/latex]

1

[latex]\Large\frac{{a}^{3}\cdot {a}^{4}}{{a}^{7}}[/latex]

[latex]{\left(\Large\frac{{x}^{2}}{{x}^{8}}\normalsize\right)}^{3}[/latex]

[latex]\Large\frac{1}{{x}^{18}}[/latex]

[latex]{\left(\Large\frac{u}{{u}^{10}}\normalsize\right)}^{2}[/latex]

[latex]{\left(\Large\frac{{a}^{4}\cdot {a}^{6}}{{a}^{3}}\normalsize\right)}^{2}[/latex]

a¹⁴

[latex]{\left(\Large\frac{{x}^{3}\cdot {x}^{8}}{{x}^{4}}\normalsize\right)}^{3}[/latex]

[latex]\Large\frac{{\left({y}^{3}\right)}^{5}}{{\left({y}^{4}\right)}^{3}}[/latex]

y³

[latex]\Large\frac{{\left({z}^{6}\right)}^{2}}{{\left({z}^{2}\right)}^{4}}[/latex]

[latex]\Large\frac{{\left({x}^{3}\right)}^{6}}{{\left({x}^{4}\right)}^{7}}[/latex]

[latex]\Large\frac{1}{{x}^{10}}[/latex]

[latex]\Large\frac{{\left({x}^{4}\right)}^{8}}{{\left({x}^{5}\right)}^{7}}[/latex]

[latex]{\left(\Large\frac{2{r}^{3}}{5s}\normalsize\right)}^{4}[/latex]

[latex]\Large\frac{16{r}^{12}}{625{s}^{4}}[/latex]

[latex]{\left(\Large\frac{3{m}^{2}}{4n}\normalsize\right)}^{3}[/latex]

[latex]{\left(\Large\frac{3{y}^{2}\cdot {y}^{5}}{{y}^{15}\cdot {y}^{8}}\normalsize\right)}^{0}[/latex]

1

[latex]{\left(\Large\frac{15{z}^{4}\cdot {z}^{9}}{0.3{z}^{2}}\normalsize\right)}^{0}[/latex]

[latex]\Large\frac{{\left({r}^{2}\right)}^{5}{\left({r}^{4}\right)}^{2}}{{\left({r}^{3}\right)}^{7}}[/latex]

[latex]\Large\frac{1}{{r}^{3}}[/latex]

[latex]\Large\frac{{\left({p}^{4}\right)}^{2}{\left({p}^{3}\right)}^{5}}{{\left({p}^{2}\right)}^{9}}[/latex]

[latex]\Large\frac{{\left(3{x}^{4}\right)}^{3}{\left(2{x}^{3}\right)}^{2}}{{\left(6{x}^{5}\right)}^{2}}[/latex]

3x⁸

[latex]\Large\frac{{\left(-2{y}^{3}\right)}^{4}{\left(3{y}^{4}\right)}^{2}}{{\left(-6{y}^{3}\right)}^{2}}[/latex]

Divide Monomials
In the following exercises, divide the monomials.

[latex]48{b}^{8}\div 6{b}^{2}[/latex]

8b⁶

[latex]42{a}^{14}\div 6{a}^{2}[/latex]

[latex]36{x}^{3}\div \left(-2{x}^{9}\right)[/latex]

[latex]\Large\frac{-18}{{x}^{6}}[/latex]

[latex]20{u}^{8}\div \left(-4{u}^{6}\right)[/latex]

[latex]\Large\frac{18{x}^{3}}{9{x}^{2}}[/latex]

2x

[latex]\Large\frac{36{y}^{9}}{4{y}^{7}}[/latex]

[latex]\Large\frac{-35{x}^{7}}{-42{x}^{13}}[/latex]

[latex]\Large\frac{5}{6{x}^{6}}[/latex]

[latex]\Large\frac{18{x}^{5}}{-27{x}^{9}}[/latex]

[latex]\Large\frac{18{r}^{5}s}{3{r}^{3}{s}^{9}}[/latex]

[latex]\Large\frac{6{r}^{2}}{{s}^{8}}[/latex]

[latex]\Large\frac{24{p}^{7}q}{6{p}^{2}{q}^{5}}[/latex]

[latex]\Large\frac{8m{n}^{10}}{64m{n}^{4}}[/latex]

[latex]\Large\frac{{n}^{6}}{8}[/latex]

[latex]\Large\frac{10{a}^{4}b}{50{a}^{2}{b}^{6}}[/latex]

[latex]\Large\frac{-12{x}^{4}{y}^{9}}{15{x}^{6}{y}^{3}}[/latex]

[latex]-\Large\frac{4{y}^{6}}{5{x}^{2}}[/latex]

[latex]\Large\frac{48{x}^{11}{y}^{9}{z}^{3}}{36{x}^{6}{y}^{8}{z}^{5}}[/latex]

[latex]\Large\frac{64{x}^{5}{y}^{9}{z}^{7}}{48{x}^{7}{y}^{12}{z}^{6}}[/latex]

[latex]\Large\frac{4z}{3{x}^{2}{y}^{3}}[/latex]

[latex]\Large\frac{\left(10{u}^{2}v\right)\left(4{u}^{3}{v}^{6}\right)}{5{u}^{9}{v}^{2}}[/latex]

[latex]\Large\frac{\left(6{m}^{2}n\right)\left(5{m}^{4}{n}^{3}\right)}{3{m}^{10}{n}^{2}}[/latex]

[latex]\Large\frac{10{n}^{2}}{{m}^{4}}[/latex]

[latex]\Large\frac{\left(6{a}^{4}{b}^{3}\right)\left(4a{b}^{5}\right)}{\left(12{a}^{8}b\right)\left({a}^{3}b\right)}[/latex]

[latex]\Large\frac{\left(4{u}^{5}{v}^{4}\right)\left(15{u}^{8}v\right)}{\left(12{u}^{3}v\right)\left({u}^{6}v\right)}[/latex]

5u⁴v³

Mixed Practice

ⓐ [latex]24{a}^{5}+2{a}^{5}[/latex]
ⓑ [latex]24{a}^{5}-2{a}^{5}[/latex]
ⓒ [latex]24{a}^{5}\cdot 2{a}^{5}[/latex]
ⓓ [latex]24{a}^{5}\div 2{a}^{5}[/latex]

ⓐ [latex]15{n}^{10}+3{n}^{10}[/latex]
ⓑ [latex]15{n}^{10}-3{n}^{10}[/latex]
ⓒ [latex]15{n}^{10}\cdot 3{n}^{10}[/latex]
ⓓ [latex]15{n}^{10}\div 3{n}^{10}[/latex]

ⓐ [latex]18{n}^{10}[/latex]
ⓑ [latex]12{n}^{10}[/latex]
ⓒ [latex]45{n}^{20}[/latex]
ⓓ [latex]5[/latex]

ⓐ [latex]{p}^{4}\cdot {p}^{6}[/latex]
ⓑ [latex]{\left({p}^{4}\right)}^{6}[/latex]

ⓐ [latex]{q}^{5}\cdot {q}^{3}[/latex]
ⓑ [latex]{\left({q}^{5}\right)}^{3}[/latex]

ⓐ [latex]{q}^{8}[/latex]
ⓑ [latex]{q}^{15}[/latex]

ⓐ [latex]\Large\frac{{y}^{3}}{y}[/latex]
ⓑ [latex]\Large\frac{y}{{y}^{3}}[/latex]

ⓐ [latex]\Large\frac{{z}^{6}}{{z}^{5}}[/latex]
ⓑ [latex]\Large\frac{{z}^{5}}{{z}^{6}}[/latex]

ⓐ [latex]z[/latex]
ⓑ [latex]\Large\frac{1}{z}[/latex]

[latex]\left(8{x}^{5}\right)\left(9x\right)\div 6{x}^{3}[/latex]

[latex]\left(4{y}^{5}\right)\left(12{y}^{7}\right)\div 8{y}^{2}[/latex]

[latex]6{y}^{6}[/latex]

[latex]\Large\frac{27{a}^{7}}{3{a}^{3}}\normalsize +\Large\frac{54{a}^{9}}{9{a}^{5}}[/latex]

[latex]\Large\frac{32{c}^{11}}{4{c}^{5}}\normalsize +\Large\frac{42{c}^{9}}{6{c}^{3}}[/latex]

[latex]15{c}^{6}[/latex]

[latex]\Large\frac{32{y}^{5}}{8{y}^{2}}\normalsize -\Large\frac{60{y}^{10}}{5{y}^{7}}[/latex]

[latex]\Large\frac{48{x}^{6}}{6{x}^{4}}\normalsize -\Large\frac{35{x}^{9}}{7{x}^{7}}[/latex]

[latex]3{x}^{2}[/latex]

[latex]\Large\frac{63{r}^{6}{s}^{3}}{9{r}^{4}{s}^{2}}\normalsize -\Large\frac{72{r}^{2}{s}^{2}}{6s}[/latex]

[latex]\Large\frac{56{y}^{4}{z}^{5}}{7{y}^{3}{z}^{3}}\normalsize -\Large\frac{45{y}^{2}{z}^{2}}{5y}[/latex]

[latex]y{z}^{2}[/latex]

Everyday Math

Memory One megabyte is approximately [latex]{10}^{6}[/latex] bytes. One gigabyte is approximately [latex]{10}^{9}[/latex] bytes. How many megabytes are in one gigabyte?

Memory One megabyte is approximately [latex]{10}^{6}[/latex] bytes. One terabyte is approximately [latex]{10}^{12}[/latex] bytes. How many megabytes are in one terabyte?

1,000,000

Writing Exercises

Vic thinks the quotient [latex]\Large\frac{{x}^{20}}{{x}^{4}}[/latex] simplifies to [latex]{x}^{5}[/latex]. What is wrong with his reasoning?

Mai simplifies the quotient [latex]\Large\frac{{y}^{3}}{y}[/latex] by writing [latex]\Large\frac{{\overline{)y}}^{3}}{\overline{)y}}=3[/latex]. What is wrong with her reasoning?

Answers will vary.

When Dimple simplified [latex]-{3}^{0}[/latex] and [latex]{\left(-3\right)}^{0}[/latex] she got the same answer. Explain how using the Order of Operations correctly gives different answers.

Roxie thinks [latex]{n}^{0}[/latex] simplifies to [latex]0[/latex]. What would you say to convince Roxie she is wrong?

Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Practice Makes Perfect

Use the Definition of a Negative Exponent
In the following exercises, simplify.

[latex]{5}^{-3}[/latex]

[latex]{8}^{-2}[/latex]

[latex]\Large\frac{1}{64}[/latex]

[latex]{3}^{-4}[/latex]

[latex]{2}^{-5}[/latex]

[latex]\Large\frac{1}{32}[/latex]

[latex]{7}^{-1}[/latex]

[latex]{10}^{-1}[/latex]

[latex]\Large\frac{1}{10}[/latex]

[latex]{2}^{-3}+{2}^{-2}[/latex]

[latex]{3}^{-2}+{3}^{-1}[/latex]

[latex]\Large\frac{4}{9}[/latex]

[latex]{3}^{-1}+{4}^{-1}[/latex]

[latex]{10}^{-1}+{2}^{-1}[/latex]

[latex]\Large\frac{3}{5}[/latex]

[latex]{10}^{0}-{10}^{-1}+{10}^{-2}[/latex]

[latex]{2}^{0}-{2}^{-1}+{2}^{-2}[/latex]

[latex]\Large\frac{3}{4}[/latex]

ⓐ [latex]{\left(-6\right)}^{-2}[/latex]
ⓑ [latex]-{6}^{-2}[/latex]

ⓐ [latex]{\left(-8\right)}^{-2}[/latex]
ⓑ [latex]-{8}^{-2}[/latex]

ⓐ [latex]\Large\frac{1}{64}[/latex]
ⓑ [latex]-\Large\frac{1}{64}[/latex]

ⓐ [latex]{\left(-10\right)}^{-4}[/latex]
ⓑ [latex]-{10}^{-4}[/latex]

ⓐ [latex]{\left(-4\right)}^{-6}[/latex]
ⓑ [latex]-{4}^{-6}[/latex]

ⓐ [latex]\Large\frac{1}{4096}[/latex]
ⓑ [latex]-\Large\frac{1}{4096}[/latex]

ⓐ [latex]5\cdot {2}^{-1}[/latex]
ⓑ [latex]{\left(5\cdot 2\right)}^{-1}[/latex]

ⓐ [latex]10\cdot {3}^{-1}[/latex]
ⓑ [latex]{\left(10\cdot 3\right)}^{-1}[/latex]

ⓐ [latex]\Large\frac{10}{3}[/latex]
ⓑ [latex]\Large\frac{1}{30}[/latex]

ⓐ [latex]4\cdot {10}^{-3}[/latex]
ⓑ [latex]{\left(4\cdot 10\right)}^{-3}[/latex]

ⓐ [latex]3\cdot {5}^{-2}[/latex]
ⓑ [latex]{\left(3\cdot 5\right)}^{-2}[/latex]

ⓐ [latex]\Large\frac{3}{25}[/latex]
ⓑ [latex]\Large\frac{1}{225}[/latex]

[latex]{n}^{-4}[/latex]

[latex]{p}^{-3}[/latex]

[latex]\Large\frac{1}{{p}^{3}}[/latex]

[latex]{c}^{-10}[/latex]

[latex]{m}^{-5}[/latex]

[latex]\Large\frac{1}{{m}^{5}}[/latex]

ⓐ [latex]4{x}^{-1}[/latex]
ⓑ [latex]{\left(4x\right)}^{-1}[/latex]
ⓒ [latex]{\left(-4x\right)}^{-1}[/latex]

ⓐ [latex]3{q}^{-1}[/latex]
ⓑ [latex]{\left(3q\right)}^{-1}[/latex]
ⓒ [latex]{\left(-3q\right)}^{-1}[/latex]

ⓐ [latex]\Large\frac{3}{q}[/latex]
ⓑ [latex]\Large\frac{1}{3q}[/latex]
ⓒ [latex]-\Large\frac{1}{3q}[/latex]

ⓐ [latex]6{m}^{-1}[/latex]
ⓑ [latex]{\left(6m\right)}^{-1}[/latex]
ⓒ [latex]{\left(-6m\right)}^{-1}[/latex]

ⓐ [latex]10{k}^{-1}[/latex]
ⓑ [latex]{\left(10k\right)}^{-1}[/latex]
ⓒ [latex]{\left(-10k\right)}^{-1}[/latex]

ⓐ [latex]\Large\frac{10}{k}[/latex]
ⓑ [latex]\Large\frac{1}{10k}[/latex]
ⓒ [latex]-\Large\frac{1}{10k}[/latex]

Simplify Expressions with Integer Exponents
In the following exercises, simplify.

[latex]{p}^{-4}\cdot {p}^{8}[/latex]

[latex]{r}^{-2}\cdot {r}^{5}[/latex]

r³

[latex]{n}^{-10}\cdot {n}^{2}[/latex]

[latex]{q}^{-8}\cdot {q}^{3}[/latex]

[latex]\Large\frac{1}{{q}^{5}}[/latex]

[latex]{k}^{-3}\cdot {k}^{-2}[/latex]

[latex]{z}^{-6}\cdot {z}^{-2}[/latex]

[latex]\Large\frac{1}{{z}^{8}}[/latex]

[latex]a\cdot {a}^{-4}[/latex]

[latex]m\cdot {m}^{-2}[/latex]

[latex]\Large\frac{1}{m}[/latex]

[latex]{p}^{5}\cdot {p}^{-2}\cdot {p}^{-4}[/latex]

[latex]{x}^{4}\cdot {x}^{-2}\cdot {x}^{-3}[/latex]

[latex]\Large\frac{1}{x}[/latex]

[latex]{a}^{3}{b}^{-3}[/latex]

[latex]{u}^{2}{v}^{-2}[/latex]

[latex]\Large\frac{{u}^{2}}{{v}^{2}}[/latex]

[latex]\left({x}^{5}{y}^{-1}\right)\left({x}^{-10}{y}^{-3}\right)[/latex]

[latex]\left({a}^{3}{b}^{-3}\right)\left({a}^{-5}{b}^{-1}\right)[/latex]

[latex]\Large\frac{1}{{a}^{2}{b}^{4}}[/latex]

[latex]\left(u{v}^{-2}\right)\left({u}^{-5}{v}^{-4}\right)[/latex]

[latex]\left(p{q}^{-4}\right)\left({p}^{-6}{q}^{-3}\right)[/latex]

[latex]\Large\frac{1}{{p}^{5}{q}^{7}}[/latex]

[latex]\left(-2{r}^{-3}{s}^{9}\right)\left(6{r}^{4}{s}^{-5}\right)[/latex]

[latex]\left(-3{p}^{-5}{q}^{8}\right)\left(7{p}^{2}{q}^{-3}\right)[/latex]

[latex]-\Large\frac{21{q}^{5}}{{p}^{3}}[/latex]

[latex]\left(-6{m}^{-8}{n}^{-5}\right)\left(-9{m}^{4}{n}^{2}\right)[/latex]

[latex]\left(-8{a}^{-5}{b}^{-4}\right)\left(-4{a}^{2}{b}^{3}\right)[/latex]

[latex]\Large\frac{32}{{a}^{3}b}[/latex]

[latex]{\left({a}^{3}\right)}^{-3}[/latex]

[latex]{\left({q}^{10}\right)}^{-10}[/latex]

[latex]\Large\frac{1}{{q}^{100}}[/latex]

[latex]{\left({n}^{2}\right)}^{-1}[/latex]

[latex]{\left({x}^{4}\right)}^{-1}[/latex]

[latex]\Large\frac{1}{{x}^{4}}[/latex]

[latex]{\left({y}^{-5}\right)}^{4}[/latex]

[latex]{\left({p}^{-3}\right)}^{2}[/latex]

[latex]\Large\frac{1}{{y}^{6}}[/latex]

[latex]{\left({q}^{-5}\right)}^{-2}[/latex]

[latex]{\left({m}^{-2}\right)}^{-3}[/latex]

m⁶

[latex]{\left(4{y}^{-3}\right)}^{2}[/latex]

[latex]{\left(3{q}^{-5}\right)}^{2}[/latex]

[latex]\Large\frac{9}{{q}^{10}}[/latex]

[latex]{\left(10{p}^{-2}\right)}^{-5}[/latex]

[latex]{\left(2{n}^{-3}\right)}^{-6}[/latex]

[latex]\Large\frac{{n}^{18}}{64}[/latex]

[latex]\Large\frac{{u}^{9}}{{u}^{-2}}[/latex]

[latex]\Large\frac{{b}^{5}}{{b}^{-3}}[/latex]

b⁸

[latex]\Large\frac{{x}^{-6}}{{x}^{4}}[/latex]

[latex]\Large\frac{{m}^{5}}{{m}^{-2}}[/latex]

m⁷

[latex]\Large\frac{{q}^{3}}{{q}^{12}}[/latex]

[latex]\Large\frac{{r}^{6}}{{r}^{9}}[/latex]

[latex]\Large\frac{1}{{r}^{3}}[/latex]

[latex]\Large\frac{{n}^{-4}}{{n}^{-10}}[/latex]

[latex]\Large\frac{{p}^{-3}}{{p}^{-6}}[/latex]

p³

Convert from Decimal Notation to Scientific Notation
In the following exercises, write each number in scientific notation.

45,000

280,000

2.8 × 10⁵

8,750,000

1,290,000

1.29 × 10⁶

0.036

0.041

4.1 × 10⁻²

0.00000924

0.0000103

1.03 × 10⁻⁵

The population of the United States on July 4, 2010 was almost [latex]310,000,000[/latex].

The population of the world on July 4, 2010 was more than [latex]6,850,000,000[/latex].

6.85 × 10⁹

The average width of a human hair is [latex]0.0018[/latex] centimeters.

The probability of winning the [latex]2010[/latex] Megamillions lottery is about [latex]0.0000000057[/latex].

5.7 × 10⁻⁹

Convert Scientific Notation to Decimal Form
In the following exercises, convert each number to decimal form.

[latex]4.1\times {10}^{2}[/latex]

[latex]8.3\times {10}^{2}[/latex]

830

[latex]5.5\times {10}^{8}[/latex]

[latex]1.6\times {10}^{10}[/latex]

16,000,000,000

[latex]3.5\times {10}^{-2}[/latex]

[latex]2.8\times {10}^{-2}[/latex]

0.028

[latex]1.93\times {10}^{-5}[/latex]

[latex]6.15\times {10}^{-8}[/latex]

0.0000000615

In 2010, the number of Facebook users each day who changed their status to ‘engaged’ was [latex]2\times {10}^{4}[/latex].

At the start of 2012, the US federal budget had a deficit of more than [latex]{$1.5}\times {10}^{13}[/latex].

$15,000,000,000,000

The concentration of carbon dioxide in the atmosphere is [latex]3.9\times {10}^{-4}[/latex].

The width of a proton is [latex]1\times {10}^{-5}[/latex] of the width of an atom.

0.00001

Multiply and Divide Using Scientific Notation
In the following exercises, multiply or divide and write your answer in decimal form.

[latex]\left(2\times {10}^{5}\right)\left(2\times {10}^{-9}\right)[/latex]

[latex]\left(3\times {10}^{2}\right)\left(1\times {10}^{-5}\right)[/latex]

0.003

[latex]\left(1.6\times {10}^{-2}\right)\left(5.2\times {10}^{-6}\right)[/latex]

[latex]\left(2.1\times {10}^{-4}\right)\left(3.5\times {10}^{-2}\right)[/latex]

0.00000735

[latex]\Large\frac{6\times {10}^{4}}{3\times {10}^{-2}}[/latex]

[latex]\Large\frac{8\times {10}^{6}}{4\times {10}^{-1}}[/latex]

200,000

[latex]\Large\frac{7\times {10}^{-2}}{1\times {10}^{-8}}[/latex]

[latex]\Large\frac{5\times {10}^{-3}}{1\times {10}^{-10}}[/latex]

50,000,000

Everyday Math

Calories In May 2010 the Food and Beverage Manufacturers pledged to reduce their products by [latex]1.5[/latex] trillion calories by the end of 2015.

1. ⓐ Write [latex]1.5[/latex] trillion in decimal notation.
2. ⓑ Write [latex]1.5[/latex] trillion in scientific notation.

Length of a year The difference between the calendar year and the astronomical year is [latex]0.000125[/latex] day.

1. ⓐ Write this number in scientific notation.
2. ⓑ How many years does it take for the difference to become 1 day?

1. ⓐ 1.25 × 10⁻⁴
2. ⓐ 8,000

Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the probability of getting a particular 5-card hand from a deck of cards, Mario divided [latex]1[/latex] by [latex]2,598,960[/latex] and saw the answer [latex]3.848\times {10}^{-7}[/latex]. Write the number in decimal notation.

Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the number of ways Barbara could make a collage with [latex]6[/latex] of her [latex]50[/latex] favorite photographs, she multiplied [latex]50\cdot 49\cdot 48\cdot 47\cdot 46\cdot 45[/latex]. Her calculator gave the answer [latex]1.1441304\times {10}^{10}[/latex]. Write the number in decimal notation.

11,441,304,000

Writing Exercises

1. ⓐ Explain the meaning of the exponent in the expression [latex]{2}^{3}[/latex].
2. ⓑ Explain the meaning of the exponent in the expression [latex]{2}^{-3}[/latex]

When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?

Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well prepared for the next section? Why or why not?

Practice Makes Perfect

Find the Greatest Common Factor of Two or More Expressions
In the following exercises, find the greatest common factor.

[latex]40,56[/latex]

[latex]45,75[/latex]

15

[latex]72,162[/latex]

[latex]150,275[/latex]

25

[latex]3x,12[/latex]

[latex]4y,28[/latex]

4

[latex]10a,50[/latex]

[latex]5b,30[/latex]

5

[latex]16y,24{y}^{2}[/latex]

[latex]9x,15{x}^{2}[/latex]

3x

[latex]18{m}^{3},36{m}^{2}[/latex]

[latex]12{p}^{4},48{p}^{3}[/latex]

12p³

[latex]10x,25{x}^{2},15{x}^{3}[/latex]

[latex]18a,6{a}^{2},22{a}^{3}[/latex]

2a

[latex]24u,6{u}^{2},30{u}^{3}[/latex]

[latex]40y,10{y}^{2},90{y}^{3}[/latex]

10y

[latex]15{a}^{4},9{a}^{5},21{a}^{6}[/latex]

[latex]35{x}^{3},10{x}^{4},5{x}^{5}[/latex]

5x³

[latex]27{y}^{2},45{y}^{3},9{y}^{4}[/latex]

[latex]14{b}^{2},35{b}^{3},63{b}^{4}[/latex]

7b²

Factor the Greatest Common Factor from a Polynomial
In the following exercises, factor the greatest common factor from each polynomial.

[latex]2x+8[/latex]

[latex]5y+15[/latex]

5(y + 3)

[latex]3a - 24[/latex]

[latex]4b - 20[/latex]

4(b − 5)

[latex]9y - 9[/latex]

[latex]7x - 7[/latex]

7(x − 1)

[latex]5{m}^{2}+20m+35[/latex]

[latex]3{n}^{2}+21n+12[/latex]

3(n² + 7n + 4)

[latex]8{p}^{2}+32p+48[/latex]

[latex]6{q}^{2}+30q+42[/latex]

6(q² + 5q + 7)

[latex]8{q}^{2}+15q[/latex]

[latex]9{c}^{2}+22c[/latex]

c(9c + 22)

[latex]13{k}^{2}+5k[/latex]

[latex]17{x}^{2}+7x[/latex]

x(17x + 7)

[latex]5{c}^{2}+9c[/latex]

[latex]4{q}^{2}+7q[/latex]

q(4q + 7)

[latex]5{p}^{2}+25p[/latex]

[latex]3{r}^{2}+27r[/latex]

3r(r + 9)

[latex]24{q}^{2}-12q[/latex]

[latex]30{u}^{2}-10u[/latex]

10u(3u − 1)

[latex]yz+4z[/latex]

[latex]ab+8b[/latex]

b(a + 8)

[latex]60x - 6{x}^{3}[/latex]

[latex]55y - 11{y}^{4}[/latex]

11y(5 − y³)

[latex]48{r}^{4}-12{r}^{3}[/latex]

[latex]45{c}^{3}-15{c}^{2}[/latex]

15c²(3c − 1)

[latex]4{a}^{3}-4a{b}^{2}[/latex]

[latex]6{c}^{3}-6c{d}^{2}[/latex]

6c(c² − d²)

[latex]30{u}^{3}+80{u}^{2}[/latex]

[latex]48{x}^{3}+72{x}^{2}[/latex]

24x²(2x + 3)

[latex]120{y}^{6}+48{y}^{4}[/latex]

[latex]144{a}^{6}+90{a}^{3}[/latex]

18a³(8a³ + 5)

[latex]4{q}^{2}+24q+28[/latex]

[latex]10{y}^{2}+50y+40[/latex]

10(y² + 5y + 4)

[latex]15{z}^{2}-30z - 90[/latex]

[latex]12{u}^{2}-36u - 108[/latex]

12(u² − 3u − 9)

[latex]3{a}^{4}-24{a}^{3}+18{a}^{2}[/latex]

[latex]5{p}^{4}-20{p}^{3}-15{p}^{2}[/latex]

5p²(p² − 4p − 3)

[latex]11{x}^{6}+44{x}^{5}-121{x}^{4}[/latex]

[latex]8{c}^{5}+40{c}^{4}-56{c}^{3}[/latex]

8c³(c² + 5c − 7)

[latex]-3n - 24[/latex]

[latex]-7p - 84[/latex]

−7(p + 12)

[latex]-15{a}^{2}-40a[/latex]

[latex]-18{b}^{2}-66b[/latex]

−6b(3b + 11)

[latex]-10{y}^{3}+60{y}^{2}[/latex]

[latex]-8{a}^{3}+32{a}^{2}[/latex]

−8a²(a − 4)

[latex]-4{u}^{5}+56{u}^{3}[/latex]

[latex]-9{b}^{5}+63{b}^{3}[/latex]

−9b³(b² − 7)

Everyday Math

Revenue A manufacturer of microwave ovens has found that the revenue received from selling microwaves a cost of [latex]p[/latex] dollars each is given by the polynomial [latex]-5{p}^{2}+150p[/latex]. Factor the greatest common factor from this polynomial.

Height of a baseball The height of a baseball hit with velocity [latex]80[/latex] feet/second at [latex]4[/latex] feet above ground level is [latex]-16{t}^{2}+80t+4[/latex], with [latex]t=[/latex] the number of seconds since it was hit. Factor the greatest common factor from this polynomial.

−4(4t² − 20t − 1)

Writing Exercises

The greatest common factor of [latex]36[/latex] and [latex]60[/latex] is [latex]12[/latex]. Explain what this means.

What is the GCF of [latex]{y}^{4}[/latex] , [latex]{y}^{5}[/latex] , and [latex]{y}^{10}[/latex] ? Write a general rule that tells how to find the GCF of [latex]{y}^{\text{a}}[/latex] , [latex]{y}^{\text{b}}[/latex] , and [latex]{y}^{\text{c}}[/latex] .

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

Chapter Review Exercises

Add and Subtract Polynomials

Identify Polynomials, Monomials, Binomials and Trinomials
In the following exercises, determine if each of the following polynomials is a monomial, binomial, trinomial, or other polynomial.

[latex]{y}^{2}+8y - 20[/latex]

trinomial

[latex]-6{a}^{4}[/latex]

[latex]9{x}^{3}-1[/latex]

binomial

[latex]{n}^{3}-3{n}^{2}+3n - 1[/latex]

Determine the Degree of Polynomials
In the following exercises, determine the degree of each polynomial.

[latex]16{x}^{2}-40x - 25[/latex]

2

[latex]5m+9[/latex]

[latex]-15[/latex]

0

[latex]{y}^{2}+6{y}^{3}+9{y}^{4}[/latex]

Add and Subtract Monomials
In the following exercises, add or subtract the monomials.

[latex]4p+11p[/latex]

15p

[latex]-8{y}^{3}-5{y}^{3}[/latex]

Add [latex]4{n}^{5},\text{-}{n}^{5},-6{n}^{5}[/latex]

−3n⁵

Subtract [latex]10{x}^{2}[/latex] from [latex]3{x}^{2}[/latex]

Add and Subtract Polynomials
In the following exercises, add or subtract the polynomials.

[latex]\left(4{a}^{2}+9a - 11\right)+\left(6{a}^{2}-5a+10\right)[/latex]

10a² + 4a − 1

[latex]\left(8{m}^{2}+12m - 5\right)-\left(2{m}^{2}-7m - 1\right)[/latex]

[latex]\left({y}^{2}-3y+12\right)+\left(5{y}^{2}-9\right)[/latex]

6y² − 3y + 3

[latex]\left(5{u}^{2}+8u\right)-\left(4u - 7\right)[/latex]

Find the sum of [latex]8{q}^{3}-27[/latex] and [latex]{q}^{2}+6q - 2[/latex]

8q³ + q² + 6q − 29

Find the difference of [latex]{x}^{2}+6x+8[/latex] and [latex]{x}^{2}-8x+15[/latex]

Evaluate a Polynomial for a Given Value of the Variable
In the following exercises, evaluate each polynomial for the given value.

[latex]200x-\Large\frac{1}{5}\normalsize{x}^{2}[/latex] when [latex]x=5[/latex]

995

[latex]200x-\Large\frac{1}{5}\normalsize{x}^{2}[/latex] when [latex]x=0[/latex]

[latex]200x-\Large\frac{1}{5}\normalsize{x}^{2}[/latex] when [latex]x=15[/latex]

2,955

[latex]5+40x-\Large\frac{1}{2}\normalsize{x}^{2}[/latex] when [latex]x=10[/latex]

[latex]5+40x-\Large\frac{1}{2}\normalsize{x}^{2}[/latex] when [latex]x=-4[/latex]

−163

[latex]5+40x-\Large\frac{1}{2}\normalsize{x}^{2}[/latex] when [latex]x=0[/latex]

A pair of glasses is dropped off a bridge [latex]640[/latex] feet above a river. The polynomial [latex]-16{t}^{2}+640[/latex] gives the height of the glasses [latex]t[/latex] seconds after they were dropped. Find the height of the glasses when [latex]t=6[/latex].

64 feet

The fuel efficiency (in miles per gallon) of a bus going at a speed of [latex]x[/latex] miles per hour is given by the polynomial [latex]-\Large\frac{1}{160}\normalsize{x}^{2}+\Large\frac{1}{2}\normalsize x[/latex]. Find the fuel efficiency when [latex]x=20[/latex] mph.

Use Multiplication Properties of Exponents

Simplify Expressions with Exponents
In the following exercises, simplify.

[latex]{6}^{3}[/latex]

216

[latex]{\left(\Large\frac{1}{2}\normalsize\right)}^{4}[/latex]

[latex]{\left(-0.5\right)}^{2}[/latex]

0.25

[latex]-{3}^{2}[/latex]

Simplify Expressions Using the Product Property of Exponents
In the following exercises, simplify each expression.

[latex]{p}^{3}\cdot {p}^{10}[/latex]

p¹³

[latex]2\cdot {2}^{6}[/latex]

[latex]a\cdot {a}^{2}\cdot {a}^{3}[/latex]

a⁶

[latex]x\cdot {x}^{8}[/latex]

Simplify Expressions Using the Power Property of Exponents
In the following exercises, simplify each expression.

[latex]{\left({y}^{4}\right)}^{3}[/latex]

y¹²

[latex]{\left({r}^{3}\right)}^{2}[/latex]

[latex]{\left({3}^{2}\right)}^{5}[/latex]

3¹⁰

[latex]{\left({a}^{10}\right)}^{y}[/latex]

Simplify Expressions Using the Product to a Power Property
In the following exercises, simplify each expression.

[latex]{\left(8n\right)}^{2}[/latex]

64n²

[latex]{\left(-5x\right)}^{3}[/latex]

[latex]{\left(2ab\right)}^{8}[/latex]

256a⁸b⁸

[latex]{\left(-10mnp\right)}^{4}[/latex]

Simplify Expressions by Applying Several Properties
In the following exercises, simplify each expression.

[latex]{\left(3{a}^{5}\right)}^{3}[/latex]

27a¹⁵

[latex]{\left(4y\right)}^{2}\left(8y\right)[/latex]

[latex]{\left({x}^{3}\right)}^{5}{\left({x}^{2}\right)}^{3}[/latex]

x²¹

[latex]{\left(5s{t}^{2}\right)}^{3}{\left(2{s}^{3}{t}^{4}\right)}^{2}[/latex]

Multiply Monomials
In the following exercises, multiply the monomials.

[latex]\left(-6{p}^{4}\right)\left(9p\right)[/latex]

−54p⁵

[latex]\left(\Large\frac{1}{3}\normalsize{c}^{2}\right)\left(30{c}^{8}\right)[/latex]

[latex]\left(8{x}^{2}{y}^{5}\right)\left(7x{y}^{6}\right)[/latex]

56x³y¹¹

[latex]\left(\Large\frac{2}{3}\normalsize{m}^{3}{n}^{6}\right)\left(\Large\frac{1}{6}\normalsize{m}^{4}{n}^{4}\right)[/latex]

Multiply Polynomials

Multiply a Polynomial by a Monomial
In the following exercises, multiply.

[latex]7\left(10-x\right)[/latex]

70 − 7x

[latex]{a}^{2}\left({a}^{2}-9a - 36\right)[/latex]

[latex]-5y\left(125{y}^{3}-1\right)[/latex]

−625y⁴ + 5y

[latex]\left(4n - 5\right)\left(2{n}^{3}\right)[/latex]

Multiply a Binomial by a Binomial
In the following exercises, multiply the binomials using various methods.

[latex]\left(a+5\right)\left(a+2\right)[/latex]

a² + 7a + 10

[latex]\left(y - 4\right)\left(y+12\right)[/latex]

[latex]\left(3x+1\right)\left(2x - 7\right)[/latex]

6x² − 19x − 7

[latex]\left(6p - 11\right)\left(3p - 10\right)[/latex]

[latex]\left(n+8\right)\left(n+1\right)[/latex]

n² + 9n + 8

[latex]\left(k+6\right)\left(k - 9\right)[/latex]

[latex]\left(5u - 3\right)\left(u+8\right)[/latex]

5u² + 37u − 24

[latex]\left(2y - 9\right)\left(5y - 7\right)[/latex]

[latex]\left(p+4\right)\left(p+7\right)[/latex]

p² + 11p + 28

[latex]\left(x - 8\right)\left(x+9\right)[/latex]

[latex]\left(3c+1\right)\left(9c - 4\right)[/latex]

27c² − 3c − 4

[latex]\left(10a - 1\right)\left(3a - 3\right)[/latex]

Multiply a Trinomial by a Binomial
In the following exercises, multiply using any method.

[latex]\left(x+1\right)\left({x}^{2}-3x - 21\right)[/latex]

x³ − 2x² − 24x − 21

[latex]\left(5b - 2\right)\left(3{b}^{2}+b - 9\right)[/latex]

[latex]\left(m+6\right)\left({m}^{2}-7m - 30\right)[/latex]

m³ − m² − 72m − 180

[latex]\left(4y - 1\right)\left(6{y}^{2}-12y+5\right)[/latex]

Divide Monomials

Simplify Expressions Using the Quotient Property of Exponents
In the following exercises, simplify.

[latex]\Large\frac{{2}^{8}}{{2}^{2}}[/latex]

2⁶or 64

[latex]\Large\frac{{a}^{6}}{a}[/latex]

[latex]\Large\frac{{n}^{3}}{{n}^{12}}[/latex]

[latex]\Large\frac{1}{{n}^{9}}[/latex]

[latex]\Large\frac{x}{{x}^{5}}[/latex]

Simplify Expressions with Zero Exponents
In the following exercises, simplify.

[latex]{3}^{0}[/latex]

1

[latex]{y}^{0}[/latex]

[latex]{\left(14t\right)}^{0}[/latex]

1

[latex]12{a}^{0}-15{b}^{0}[/latex]

Simplify Expressions Using the Quotient to a Power Property
In the following exercises, simplify.

[latex]{\left(\Large\frac{3}{5}\normalsize\right)}^{2}[/latex]

[latex]\Large\frac{9}{25}[/latex]

[latex]{\left(\Large\frac{x}{2}\normalsize\right)}^{5}[/latex]

[latex]{\left(\Large\frac{5m}{n}\normalsize\right)}^{3}[/latex]

[latex]\Large\frac{125{m}^{3}}{{n}^{3}}[/latex]

[latex]{\left(\Large\frac{s}{10t}\normalsize\right)}^{2}[/latex]

Simplify Expressions by Applying Several Properties
In the following exercises, simplify.

[latex]\Large\frac{{\left({a}^{3}\right)}^{2}}{{a}^{4}}[/latex]

a²

[latex]\Large\frac{{u}^{3}}{{u}^{2}\normalsize\cdot {u}^{4}}[/latex]

[latex]{\left(\Large\frac{x}{{x}^{9}}\normalsize\right)}^{5}[/latex]

[latex]\Large\frac{1}{{x}^{40}}[/latex]

[latex]{\left(\Large\frac{{p}^{4}\cdot {p}^{5}}{{p}^{3}}\normalsize\right)}^{2}[/latex]

[latex]\Large\frac{{\left({n}^{5}\right)}^{3}}{{\left({n}^{2}\right)}^{8}}[/latex]

[latex]\Large\frac{1}{n}[/latex]

[latex]{\left(\Large\frac{5{s}^{2}}{4t}\normalsize\right)}^{3}[/latex]

Divide Monomials
In the following exercises, divide the monomials.

[latex]72{p}^{12}\div 8{p}^{3}[/latex]

9p⁹

[latex]-26{a}^{8}\div \left(2{a}^{2}\right)[/latex]

[latex]\Large\frac{45{y}^{6}}{-15{y}^{10}}[/latex]

[latex]-\Large\frac{3}{{y}^{4}}[/latex]

[latex]\Large\frac{-30{x}^{8}}{-36{x}^{9}}[/latex]

[latex]\Large\frac{28{a}^{9}b}{7{a}^{4}{b}^{3}}[/latex]

[latex]\Large\frac{4{a}^{5}}{{b}^{2}}[/latex]

[latex]\Large\frac{11{u}^{6}{v}^{3}}{55{u}^{2}{v}^{8}}[/latex]

[latex]\Large\frac{\left(5{m}^{9}{n}^{3}\right)\left(8{m}^{3}{n}^{2}\right)}{\left(10m{n}^{4}\right)\left({m}^{2}{n}^{5}\right)}[/latex]

[latex]\Large\frac{4{m}^{9}}{{n}^{4}}[/latex]

[latex]\Large\frac{42{r}^{2}{s}^{4}}{6r{s}^{3}}\normalsize -\Large\frac{54r{s}^{2}}{9s}[/latex]

Integer Exponents and Scientific Notation

Use the Definition of a Negative Exponent
In the following exercises, simplify.

[latex]{6}^{-2}[/latex]

[latex]\Large\frac{1}{36}[/latex]

[latex]{\left(-10\right)}^{-3}[/latex]

[latex]5\cdot {2}^{-4}[/latex]

[latex]\Large\frac{5}{16}[/latex]

[latex]{\left(8n\right)}^{-1}[/latex]

Simplify Expressions with Integer Exponents
In the following exercises, simplify.

[latex]{x}^{-3}\cdot {x}^{9}[/latex]

x⁶

[latex]{r}^{-5}\cdot {r}^{-4}[/latex]

[latex]\left(u{v}^{-3}\right)\left({u}^{-4}{v}^{-2}\right)[/latex]

[latex]\Large\frac{1}{{u}^{3}{v}^{5}}[/latex]

[latex]{\left({m}^{5}\right)}^{-1}[/latex]

[latex]{\left({k}^{-2}\right)}^{-3}[/latex]

k⁶

[latex]\Large\frac{{q}^{4}}{{q}^{20}}[/latex]

[latex]\Large\frac{{b}^{8}}{{b}^{-2}}[/latex]

b¹⁰

[latex]\Large\frac{{n}^{-3}}{{n}^{-5}}[/latex]

Convert from Decimal Notation to Scientific Notation
In the following exercises, write each number in scientific notation.

[latex]5,300,000[/latex]

5.3 × 10⁶

[latex]0.00814[/latex]

The thickness of a piece of paper is about [latex]0.097[/latex] millimeter.

9.7 × 10⁻²

According to www.cleanair.com, U.S. businesses use about [latex]21,000,000[/latex] tons of paper per year.

Convert Scientific Notation to Decimal Form
In the following exercises, convert each number to decimal form.

[latex]2.9\times {10}^{4}[/latex]

29,000

[latex]1.5\times {10}^{8}[/latex]

[latex]3.75\times {10}^{-1}[/latex]

375

[latex]9.413\times {10}^{-5}[/latex]

Multiply and Divide Using Scientific Notation
In the following exercises, multiply and write your answer in decimal form.

[latex]\left(3\times {10}^{7}\right)\left(2\times {10}^{-4}\right)[/latex]

6,000

[latex]\left(1.5\times {10}^{-3}\right)\left(4.8\times {10}^{-1}\right)[/latex]

[latex]\Large\frac{6\times {10}^{9}}{2\times {10}^{-1}}[/latex]

30,000,000,000

[latex]\Large\frac{9\times {10}^{-3}}{1\times {10}^{-6}}[/latex]

Introduction to Factoring Polynomials

Find the Greatest Common Factor of Two or More Expressions
In the following exercises, find the greatest common factor.

[latex]5n,45[/latex]

5

[latex]8a,72[/latex]

[latex]12{x}^{2},20{x}^{3},36{x}^{4}[/latex]

4x²

[latex]9{y}^{4},21{y}^{5},15{y}^{6}[/latex]

Factor the Greatest Common Factor from a Polynomial
In the following exercises, factor the greatest common factor from each polynomial.

[latex]16u - 24[/latex]

8(2u − 3)

[latex]15r+35[/latex]

[latex]6{p}^{2}+6p[/latex]

6p(p + 1)

[latex]10{c}^{2}-10c[/latex]

[latex]-9{a}^{5}-9{a}^{3}[/latex]

−9a³(a² + 1)

[latex]-7{x}^{8}-28{x}^{3}[/latex]

[latex]5{y}^{2}-55y+45[/latex]

5(y² − 11y + 9)

[latex]2{q}^{5}-16{q}^{3}+30{q}^{2}[/latex]

Chapter Practice Test

For the polynomial [latex]8{y}^{4}-3{y}^{2}+1[/latex]

1. ⓐ Is it a monomial, binomial, or trinomial?
2. ⓑ What is its degree?

1. ⓐ trinomial
2. ⓑ 4

In the following exercises, simplify each expression.

[latex]\left(5{a}^{2}+2a - 12\right)+\left(9{a}^{2}+8a - 4\right)[/latex]

[latex]\left(10{x}^{2}-3x+5\right)-\left(4{x}^{2}-6\right)[/latex]

6x² − 3x + 11

[latex]{\left(-\Large\frac{3}{4}\normalsize\right)}^{3}[/latex]

[latex]n\cdot {n}^{4}[/latex]

n⁵

[latex]{\left(10{p}^{3}{q}^{5}\right)}^{2}[/latex]

[latex]\left(8x{y}^{3}\right)\left(-6{x}^{4}{y}^{6}\right)[/latex]

−48x⁵y⁹

[latex]4u\left({u}^{2}-9u+1\right)[/latex]

[latex]\left(s+8\right)\left(s+9\right)[/latex]

s² + 17s + 72

[latex]\left(m+3\right)\left(7m - 2\right)[/latex]

[latex]\left(11a - 6\right)\left(5a - 1\right)[/latex]

55a² − 41a + 6

[latex]\left(n - 8\right)\left({n}^{2}-4n+11\right)[/latex]

[latex]\left(4a+9b\right)\left(6a - 5b\right)[/latex]

24a² + 34ab − 45b²

[latex]\Large\frac{{5}^{6}}{{5}^{8}}[/latex]

[latex]{\left(\Large\frac{{x}^{3}\cdot {x}^{9}}{{x}^{5}}\normalsize\right)}^{2}[/latex]

x¹⁴

[latex]{\left(47{a}^{18}{b}^{23}{c}^{5}\right)}^{0}[/latex]

[latex]\Large\frac{24{r}^{3}s}{6{r}^{2}{s}^{7}}[/latex]

[latex]\Large\frac{4r}{{s}^{6}}[/latex]

[latex]\Large\frac{8{y}^{2}-16y+20}{4y}[/latex]

[latex]\left(15x{y}^{3}-35{x}^{2}y\right)\div 5xy[/latex]

3y² − 7x

[latex]{4}^{-1}[/latex]

[latex]{\left(2y\right)}^{-3}[/latex]

[latex]\Large\frac{1}{2y}[/latex]

[latex]{p}^{-3}\cdot {p}^{-8}[/latex]

[latex]\Large\frac{{x}^{4}}{{x}^{-5}}[/latex]

x⁹

[latex]\left(2.4\times {10}^{8}\right)\left(2\times {10}^{-5}\right)[/latex]

In the following exercises, factor the greatest common factor from each polynomial.

[latex]80{a}^{3}+120{a}^{2}+40a[/latex]

[latex]-6{x}^{2}-30x[/latex]

−6x(x + 5)

Convert [latex]5.25\times {10}^{-4}[/latex] to decimal form.

0.000525

In the following exercises, simplify, and write your answer in decimal form.

[latex]\Large\frac{9\times {10}^{4}}{3\times {10}^{-1}}[/latex]

3 × 10⁵

A hiker drops a pebble from a bridge [latex]240[/latex] feet above a canyon. The polynomial [latex]-16{t}^{2}+240[/latex] gives the height of the pebble [latex]t[/latex] seconds a after it was dropped. Find the height when [latex]t=3[/latex].

According to www.cleanair.org, the amount of trash generated in the US in one year averages out to [latex]112,000[/latex] pounds of trash per person. Write this number in scientific notation.