Classes of Real Numbers
Rational Numbers
In the following exercises, write as the ratio of two integers.
- ⓐ [latex]5[/latex]
- ⓑ [latex]3.19[/latex]
- ⓐ [latex]\Large\frac{5}{1}[/latex]
- ⓑ [latex]\Large\frac{319}{100}[/latex]
- ⓐ [latex]8[/latex]
- ⓑ [latex]-1.61[/latex]
- ⓐ [latex]-12[/latex]
- ⓑ [latex]9.279[/latex]
- ⓐ [latex]\Large\frac{-12}{1}[/latex]
- ⓑ [latex]\Large\frac{9279}{1000}[/latex]
- ⓐ [latex]-16[/latex]
- ⓑ [latex]4.399[/latex]
In the following exercises, determine which of the given numbers are rational and which are irrational.
[latex]0.75[/latex] , [latex]0.22\stackrel{\text{-}}{\text{3}}[/latex] , [latex]\text{1.39174... }[/latex]
Rational: [latex]0.75,0.22\stackrel{\text{-}}{\text{3}}[/latex] . Irrational: [latex]\text{1.39174... }[/latex]
[latex]0.36[/latex] , [latex]\text{0.94729\ldots }[/latex] , [latex]2.52\stackrel{\text{-}}{\text{8}}[/latex]
[latex]0.\stackrel{\text{-}}{45}[/latex] , [latex]\text{1.919293... }[/latex] , [latex]3.59[/latex]
Rational: [latex]0.\stackrel{\text{-}}{45}[/latex] , [latex]3.59[/latex] . Irrational: [latex]\text{1.919293... }[/latex]
[latex]0.1\stackrel{\text{-}}{\text{3}},\text{0.42982... }[/latex] , [latex]1.875[/latex]
In the following exercises, identify whether each number is rational or irrational.
- ⓐ [latex]\sqrt{25}[/latex]
- ⓑ [latex]\sqrt{30}[/latex]
- ⓐ rational
- ⓑ irrational
- ⓐ [latex]\sqrt{44}[/latex]
- ⓑ [latex]\sqrt{49}[/latex]
- ⓐ [latex]\sqrt{164}[/latex]
- ⓑ [latex]\sqrt{169}[/latex]
- ⓐ irrational
- ⓑ rational
- ⓐ [latex]\sqrt{225}[/latex]
- ⓑ [latex]\sqrt{216}[/latex]
Classifying Real Numbers
In the following exercises, determine whether each number is whole, integer, rational, irrational, and real.
[latex]-8[/latex] , [latex]0,\text{1.95286....}[/latex] , [latex]\Large\frac{12}{5}[/latex] , [latex]\sqrt{36}[/latex] , [latex]9[/latex]

[latex]-9[/latex] , [latex]-3\Large\frac{4}{9}[/latex] , [latex]-\sqrt{9}[/latex] , [latex]0.4\stackrel{\text{-}}{09}[/latex] , [latex]\Large\frac{11}{6}[/latex] , [latex]7[/latex]
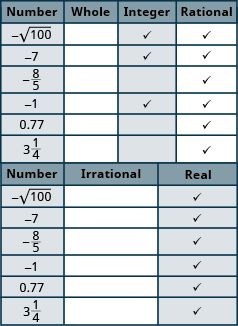
[latex]-\sqrt{100}[/latex] , [latex]-7[/latex] , [latex]-\Large\frac{8}{3}[/latex] , [latex]-1[/latex] , [latex]0.77[/latex] , [latex]3\Large\frac{1}{4}[/latex]
EVERYDAY MATH
Field trip
All the [latex]5\text{th}[/latex] graders at Lincoln Elementary School will go on a field trip to the science museum. Counting all the children, teachers, and chaperones, there will be [latex]147[/latex] people. Each bus holds [latex]44[/latex] people.
ⓐ How many buses will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn’t you round the answer the usual way?
Child care
Serena wants to open a licensed child care center. Her state requires that there be no more than [latex]12[/latex] children for each teacher. She would like her child care center to serve [latex]40[/latex] children.
ⓐ How many teachers will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn’t you round the answer the usual way?
ⓐ 4
ⓑ Teachers cannot be divided
ⓒ It would result in a lower number.
WRITING EXERCISES
In your own words, explain the difference between a rational number and an irrational number.
Explain how the sets of numbers (counting, whole, integer, rational, irrationals, reals) are related to each other.
Answers will vary.
Using the Commutative and Associative Properties
In the following exercises, use the commutative properties to rewrite the given expression.
[latex]\text{8+9=___}[/latex]
[latex]\text{7+6=___}[/latex]
7 + 6 = 6 + 7
[latex]\text{8}\left(-12\right)\text{=___}[/latex]
[latex]\text{7}\left(-13\right)\text{=___}[/latex]
7(−13) = (−13)7
[latex]\text{(-19)(-14)=___}[/latex]
[latex]\left(-12\right)\left(-18\right)\text{=___}[/latex]
(−12)(−18) = (−18)(−12)
[latex]\text{-11+8=___}[/latex]
[latex]\text{-15+7=___}[/latex]
−15 + 7 = 7 + (−15)
[latex]\text{x+4=___}[/latex]
[latex]\text{y+1=___}[/latex]
y + 1 = 1 + y
[latex]\text{-2a=___}[/latex]
[latex]\text{-3m=___}[/latex]
−3m = m(−3)
In the following exercises, use the associative properties to rewrite the given expression.
[latex]\left(11+9\right)\text{+14=___}[/latex]
[latex]\left(21+14\right)\text{+9=___}[/latex]
(21 + 14) + 9 = 21 + (14 + 9)
[latex]\left(12\cdot 5\right)\cdot \text{7=___}[/latex]
[latex]\left(14\cdot 6\right)\cdot \text{9=___}[/latex]
(14 · 6) · 9 = 14(6 · 9)
[latex]\left(-7+9\right)\text{+8=___}[/latex]
[latex]\left(-2+6\right)\text{+7=___}[/latex]
(−2 + 6) + 7 = −2 + (6 + 7)
[latex]\left(16\cdot\Large\frac{4}{5}\normalsize\right)\cdot \text{15=___}[/latex]
[latex]\left(13\cdot\Large\frac{2}{3}\normalsize\right)\cdot \text{18=___}[/latex]
[latex]\left(13\cdot\Large\frac{2}{3}\normalsize\right)\cdot 18=13\left(\Large\frac{2}{3}\normalsize\cdot 18\right)[/latex]
[latex]3\left(4x\right)\text{=___}[/latex]
[latex]4\left(7x\right)\text{=___}[/latex]
4(7x) = (4 · 7)x
[latex]\left(12+x\right)\text{+28=___}[/latex]
[latex]\left(17+y\right)\text{+33=___}[/latex]
(17 + y) + 33 = 17 + (y + 33)
Evaluate Expressions using the Commutative and Associative Properties
In the following exercises, evaluate each expression for the given value.
If [latex]y=\Large\frac{5}{8}[/latex], evaluate:
ⓐ [latex]y+0.49+\left(-y\right)[/latex]
ⓑ [latex]y+\left(-y\right)+0.49[/latex]
If [latex]z=\Large\frac{7}{8}[/latex], evaluate:
ⓐ [latex]z+0.97+\left(-z\right)[/latex]
ⓑ [latex]z+\left(-z\right)+0.97[/latex]
- ⓐ 0.97
- ⓑ 0.97
If [latex]c=-\Large\frac{11}{4}[/latex], evaluate:
ⓐ [latex]c+3.125+\left(-c\right)[/latex]
ⓑ [latex]c+\left(-c\right)+3.125[/latex]
If [latex]d=-\Large\frac{9}{4}[/latex], evaluate:
ⓐ [latex]d+2.375+\left(-d\right)[/latex]
ⓑ [latex]d+\left(-d\right)+2.375[/latex]
ⓐ 2.375
ⓑ 2.375
If [latex]j=11[/latex], evaluate:
ⓐ [latex]\Large\frac{5}{6}\left(\frac{6}{5}\normalsize j\Large\right)[/latex]
ⓑ [latex]\Large\left(\frac{5}{6}\normalsize\cdot\Large\frac{6}{5}\right)\normalsize j[/latex]
If [latex]k=21[/latex], evaluate:
ⓐ [latex]\Large\frac{4}{13}\left(\frac{13}{4}\normalsize k\Large\right)[/latex]
ⓑ [latex]\Large\left(\frac{4}{13}\normalsize\cdot\Large\frac{13}{4}\right)\normalsize k[/latex]
ⓐ 21
ⓑ 21
If [latex]m=-25[/latex], evaluate:
ⓐ [latex]-\Large\frac{3}{7}\left(\frac{7}{3}\normalsize m\Large\right)[/latex]
ⓑ [latex]\Large\left(-\frac{3}{7}\normalsize\cdot\Large\frac{7}{3}\right)\normalsize m[/latex]
If [latex]n=-8[/latex], evaluate:
ⓐ [latex]-\Large\frac{5}{21}\left(\frac{21}{5}\normalsize n\Large\right)[/latex]
ⓑ [latex]\Large\left(-\frac{5}{21}\normalsize\cdot\Large\frac{21}{5}\right)\normalsize n[/latex]
ⓐ −8
ⓑ −8
Simplify Expressions Using the Commutative and Associative Properties
In the following exercises, simplify.
[latex]-45a+15+45a[/latex]
[latex]9y+23+\left(-9y\right)[/latex]
23
[latex]\Large\frac{1}{2}\normalsize +\Large\frac{7}{8}\normalsize +\Large\left(-\frac{1}{2}\right)[/latex]
[latex]\Large\frac{2}{5}\normalsize +\Large\frac{5}{12}\normalsize+\Large\left(-\frac{2}{5}\right)[/latex]
[latex]\Large\frac{5}{12}[/latex]
[latex]\Large\frac{3}{20}\normalsize\cdot\Large\frac{49}{11}\normalsize\cdot\Large\frac{20}{3}[/latex]
[latex]\Large\frac{13}{18}\normalsize\cdot\Large\frac{25}{7}\normalsize\cdot\Large\frac{18}{13}[/latex]
[latex]\Large\frac{25}{7}[/latex]
[latex]\Large\frac{7}{12}\normalsize\cdot\Large\frac{9}{17}\normalsize\cdot\Large\frac{24}{7}[/latex]
[latex]\Large\frac{3}{10}\normalsize\cdot\Large\frac{13}{23}\normalsize\cdot\Large\frac{50}{3}[/latex]
[latex]\Large\frac{65}{23}[/latex]
[latex]-24\cdot 7\cdot\Large\frac{3}{8}[/latex]
[latex]-36\cdot 11\cdot\Large\frac{4}{9}[/latex]
−176
[latex]\Large\left(\frac{5}{6}\normalsize +\Large\frac{8}{15}\right)\normalsize +\Large\frac{7}{15}[/latex]
[latex]\Large\left(\frac{1}{12}\normalsize +\Large\frac{4}{9}\right)\normalsize +\Large\frac{5}{9}[/latex]
[latex]\Large\frac{13}{12}[/latex]
[latex]\Large\frac{5}{13}\normalsize +\Large\frac{3}{4}\normalsize +\Large\frac{1}{4}[/latex]
[latex]\Large\frac{8}{15}\normalsize +\Large\frac{5}{7}\normalsize +\Large\frac{2}{7}[/latex]
[latex]\Large\frac{23}{15}[/latex]
[latex]\left(4.33p+1.09p\right)+3.91p[/latex]
[latex]\left(5.89d+2.75d\right)+1.25d[/latex]
9.89d
[latex]17\left(0.25\right)\left(4\right)[/latex]
[latex]36\left(0.2\right)\left(5\right)[/latex]
36
[latex]\left[2.48\left(12\right)\right]\left(0.5\right)[/latex]
[latex]\left[9.731\left(4\right)\right]\left(0.75\right)[/latex]
29.193
[latex]7\left(4a\right)[/latex]
[latex]9\left(8w\right)[/latex]
72w
[latex]-15\left(5m\right)[/latex]
[latex]-23\left(2n\right)[/latex]
−46n
[latex]12\left(\Large\frac{5}{6}\normalsize p\right)[/latex]
[latex]20\left(\Large\frac{3}{5}\normalsize q\right)[/latex]
12q
[latex]14x+19y+25x+3y[/latex]
[latex]15u+11v+27u+19v[/latex]
42u + 30v
[latex]43m+\left(-12n\right)+\text{ }\left(-16m\right)+\left(-9n\right)[/latex]
[latex]-22p+17q+\left(-35p\right)+\left(-27q\right)[/latex]
−57p + (−10q)
[latex]\Large\frac{3}{8}\normalsize g+\Large\frac{1}{12}\normalsize h+\Large\frac{7}{8}\normalsize g+\Large\frac{5}{12}\normalsize h[/latex]
[latex]\Large\frac{5}{6}\normalsize a+\Large\frac{3}{10}\normalsize b+\Large\frac{1}{6}\normalsize a+\Large\frac{9}{10}\normalsize b[/latex]
[latex]a+\Large\frac{6}{5}\normalsize b[/latex]
[latex]6.8p+9.14q+\left(-4.37p\right)+\left(-0.88q\right)[/latex]
[latex]9.6m+7.22n+\left(-2.19m\right)+\left(-0.65n\right)[/latex]
7.41m + 6.57n
EVERYDAY MATH
Stamps
Allie and Loren need to buy stamps. Allie needs four [latex]{$0.49}[/latex] stamps and nine [latex]{$0.02}[/latex] stamps. Loren needs eight [latex]{$0.49}[/latex] stamps and three [latex]{$0.02}[/latex] stamps.
ⓐ How much will Allie’s stamps cost?
ⓑ How much will Loren’s stamps cost?
ⓒ What is the total cost of the girls’ stamps?
ⓓ How many [latex]{$0.49}[/latex] stamps do the girls need altogether? How much will they cost?
ⓔ How many [latex]{$0.02}[/latex] stamps do the girls need altogether? How much will they cost?
Counting Cash
Grant is totaling up the cash from a fundraising dinner. In one envelope, he has twenty-three [latex]{$5}[/latex] bills, eighteen [latex]{$10}[/latex] bills, and thirty-four [latex]{$20}[/latex] bills. In another envelope, he has fourteen [latex]{$5}[/latex] bills, nine [latex]{$10}[/latex] bills, and twenty-seven [latex]{$20}[/latex] bills.
ⓐ How much money is in the first envelope?
ⓑ How much money is in the second envelope?
ⓒ What is the total value of all the cash?
ⓓ What is the value of all the [latex]{$5}[/latex] bills?
ⓔ What is the value of all [latex]{$10}[/latex] bills?
ⓕ What is the value of all [latex]{$20}[/latex] bills?
- ⓐ $975
- ⓑ $700
- ⓒ $1675
- ⓓ $185
- ⓔ $270
- ⓕ $1220
WRITING EXERCISES
In your own words, state the Commutative Property of Addition and explain why it is useful.
In your own words, state the Associative Property of Multiplication and explain why it is useful.
Answers will vary.
Using the Distributive Property
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the distributive property.
[latex]4\left(x+8\right)[/latex]
[latex]3\left(a+9\right)[/latex]
3a + 27
[latex]8\left(4y+9\right)[/latex]
[latex]9\left(3w+7\right)[/latex]
27w + 63
[latex]6\left(c - 13\right)[/latex]
[latex]7\left(y - 13\right)[/latex]
7y − 91
[latex]7\left(3p - 8\right)[/latex]
[latex]5\left(7u - 4\right)[/latex]
35u − 20
[latex]\Large\frac{1}{2}\normalsize\left(n+8\right)[/latex]
[latex]\Large\frac{1}{3}\normalsize\left(u+9\right)[/latex]
[latex]\Large\frac{1}{3}\normalsize u+3[/latex]
[latex]\Large\frac{1}{4}\normalsize\left(3q+12\right)[/latex]
[latex]\Large\frac{1}{5}\normalsize\left(4m+20\right)[/latex]
[latex]\Large\frac{4}{5}\normalsize m+4[/latex]
[latex]9\left(\Large\frac{5}{9}\normalsize y-\Large\frac{1}{3}\normalsize\right)[/latex]
[latex]10\left(\Large\frac{3}{10}\normalsize x-\Large\frac{2}{5}\normalsize\right)[/latex]
3x − 4
[latex]12\left(\Large\frac{1}{4}\normalsize+\Large\frac{2}{3}\normalsize r\right)[/latex]
[latex]12\left(\Large\frac{1}{6}\normalsize +\Large\frac{3}{4}\normalsize s\right)[/latex]
2 + 9s
[latex]r\left(s - 18\right)[/latex]
[latex]u\left(v - 10\right)[/latex]
uv − 10u
[latex]\left(y+4\right)p[/latex]
[latex]\left(a+7\right)x[/latex]
ax + 7x
[latex]-2\left(y+13\right)[/latex]
[latex]-3\left(a+11\right)[/latex]
−3a − 33
[latex]-7\left(4p+1\right)[/latex]
[latex]-9\left(9a+4\right)[/latex]
−81a − 36
[latex]-3\left(x - 6\right)[/latex]
[latex]-4\left(q - 7\right)[/latex]
−4q + 28
[latex]-9\left(3a - 7\right)[/latex]
[latex]-6\left(7x - 8\right)[/latex]
−42x + 48
[latex]-\left(r+7\right)[/latex]
[latex]-\left(q+11\right)[/latex]
−q − 11
[latex]-\left(3x - 7\right)[/latex]
[latex]-\left(5p - 4\right)[/latex]
−5p + 4
[latex]5+9\left(n - 6\right)[/latex]
[latex]12+8\left(u - 1\right)[/latex]
8u + 4
[latex]16 - 3\left(y+8\right)[/latex]
[latex]18 - 4\left(x+2\right)[/latex]
−4x + 10
[latex]4 - 11\left(3c - 2\right)[/latex]
[latex]9 - 6\left(7n - 5\right)[/latex]
−42n + 39
[latex]22-\left(a+3\right)[/latex]
[latex]8-\left(r - 7\right)[/latex]
−r + 15
[latex]-12-\left(u+10\right)[/latex]
[latex]-4-\left(c - 10\right)[/latex]
−c + 6
[latex]\left(5m - 3\right)-\left(m+7\right)[/latex]
[latex]\left(4y - 1\right)-\left(y - 2\right)[/latex]
3y + 1
[latex]5\left(2n+9\right)+12\left(n - 3\right)[/latex]
[latex]9\left(5u+8\right)+2\left(u - 6\right)[/latex]
47u + 60
[latex]9\left(8x - 3\right)-\left(-2\right)[/latex]
[latex]4\left(6x - 1\right)-\left(-8\right)[/latex]
24x + 4
[latex]14\left(c - 1\right)-8\left(c - 6\right)[/latex]
[latex]11\left(n - 7\right)-5\left(n - 1\right)[/latex]
6n − 72
[latex]6\left(7y+8\right)-\left(30y - 15\right)[/latex]
[latex]7\left(3n+9\right)-\left(4n - 13\right)[/latex]
17n + 76
Evaluate Expressions Using the Distributive Property
In the following exercises, evaluate both expressions for the given value.
If [latex]v=-2[/latex], evaluate
ⓐ [latex]6\left(4v+7\right)[/latex]
ⓑ [latex]6\cdot 4v+6\cdot 7[/latex]
If [latex]u=-1[/latex], evaluate
ⓐ [latex]8\left(5u+12\right)[/latex]
ⓑ [latex]8\cdot 5u+8\cdot 12[/latex]
ⓐ 56
ⓑ 56
If [latex]n=\Large\frac{2}{3}[/latex], evaluate
ⓐ [latex]3\left(n+\Large\frac{5}{6}\normalsize\right)[/latex]
ⓑ [latex]3\cdot n+3\cdot\Large\frac{5}{6}[/latex]
If [latex]y=\Large\frac{3}{4}[/latex], evaluate
ⓐ [latex]4\left(y+\Large\frac{3}{8}\normalsize\right)[/latex]
ⓑ [latex]4\cdot y+4\cdot\Large\frac{3}{8}[/latex]
ⓐ [latex]\Large\frac{9}{2}[/latex]
ⓑ [latex]\Large\frac{9}{2}[/latex]
If [latex]y=\Large\frac{7}{12}[/latex], evaluate
ⓐ [latex]-3\left(4y+15\right)[/latex]
ⓑ [latex]3\cdot 4y+\left(-3\right)\cdot 15[/latex]
If [latex]p=\Large\frac{23}{30}[/latex], evaluate
ⓐ [latex]-6\left(5p+11\right)[/latex]
ⓑ [latex]-6\cdot 5p+\left(-6\right)\cdot 11[/latex]
ⓐ −89
ⓑ −89
If [latex]m=0.4[/latex], evaluate
ⓐ [latex]-10\left(3m - 0.9\right)[/latex]
ⓑ [latex]-10\cdot 3m-\left(-10\right)\left(0.9\right)[/latex]
If [latex]n=0.75[/latex], evaluate
ⓐ [latex]-100\left(5n+1.5\right)[/latex]
ⓑ [latex]-100\cdot 5n+\left(-100\right)\left(1.5\right)[/latex]
ⓐ −525
ⓑ −525
If [latex]y=-25[/latex], evaluate
ⓐ [latex]-\left(y - 25\right)[/latex]
ⓑ [latex]-y+25[/latex]
If [latex]w=-80[/latex], evaluate
ⓐ [latex]-\left(w - 80\right)[/latex]
ⓑ [latex]-w+80[/latex]
ⓐ 160
ⓑ 160
If [latex]p=0.19[/latex], evaluate
ⓐ [latex]-\left(p+0.72\right)[/latex]
ⓑ [latex]-p - 0.72[/latex]
If [latex]q=0.55[/latex], evaluate
ⓐ [latex]-\left(q+0.48\right)[/latex]
ⓑ [latex]-q - 0.48[/latex]
ⓐ −1.03
ⓑ −1.03
EVERYDAY MATH
Buying by the case
Joe can buy his favorite ice tea at a convenience store for [latex]{$1.99}[/latex] per bottle. At the grocery store, he can buy a case of [latex]12[/latex] bottles for [latex]{$23.88}[/latex].
ⓐ Use the distributive property to find the cost of [latex]12[/latex] bottles bought individually at the convenience store. (Hint: notice that [latex]{$1.99}[/latex] is [latex]{$2}-{$0.01}[/latex]. )
ⓑ Is it a bargain to buy the iced tea at the grocery store by the case?
Multi-pack purchase
Adele’s shampoo sells for [latex]{$3.97}[/latex] per bottle at the drug store. At the warehouse store, the same shampoo is sold as a [latex]{3-pack}[/latex] for [latex]{$10.49}[/latex].
ⓐ Show how you can use the distributive property to find the cost of [latex]3[/latex] bottles bought individually at the drug store.
ⓑ How much would Adele save by buying the [latex]{3-pack}[/latex] at the warehouse store?
ⓐ 3(4 − 0.03) = 11.91
ⓑ $1.42
WRITING EXERCISES
Simplify [latex]8\left(x-\Large\frac{1}{4}\normalsize\right)[/latex] using the distributive property and explain each step.
Explain how you can multiply [latex]4\left({$5.97}\right)[/latex] without paper or a calculator by thinking of [latex]{$5.97}[/latex] as [latex]6 - 0.03[/latex] and then using the distributive property.
Properties of Identity, Inverses, and Zero
In the following exercises, identify whether each example is using the identity property of addition or multiplication.
[latex]101+0=101[/latex]
[latex]\Large\frac{3}{5}\normalsize\left(1\right)=\Large\frac{3}{5}[/latex]
identity property of multiplication
[latex]-9\cdot 1=-9[/latex]
[latex]0+64=64[/latex]
identity property of addition
Use the Inverse Properties of Addition and Multiplication
In the following exercises, find the multiplicative inverse.
[latex]8[/latex]
[latex]14[/latex]
[latex]\Large\frac{1}{14}[/latex]
[latex]-17[/latex]
[latex]-19[/latex]
[latex]-\Large\frac{1}{19}[/latex]
[latex]\Large\frac{7}{12}[/latex]
[latex]\Large\frac{8}{13}[/latex]
[latex]\Large\frac{13}{8}[/latex]
[latex]-\Large\frac{3}{10}[/latex]
[latex]-\Large\frac{5}{12}[/latex]
[latex]-\Large\frac{12}{5}[/latex]
[latex]0.8[/latex]
[latex]0.4[/latex]
[latex]\Large\frac{5}{2}[/latex]
[latex]-0.2[/latex]
[latex]-0.5[/latex]
−2
Use the Properties of Zero
In the following exercises, simplify using the properties of zero.
[latex]48\cdot 0[/latex]
[latex]\Large\frac{0}{6}[/latex]
0
[latex]\Large\frac{3}{0}[/latex]
[latex]22\cdot 0[/latex]
0
[latex]0\div\Large\frac{11}{12}[/latex]
[latex]\Large\frac{6}{0}[/latex]
undefined
[latex]\Large\frac{0}{3}[/latex]
[latex]0\div\Large\frac{7}{15}[/latex]
0
[latex]0\cdot\Large\frac{8}{15}[/latex]
[latex]\left(-3.14\right)\left(0\right)[/latex]
0
[latex]5.72\div 0[/latex]
[latex]\Large\frac{\frac{1}{10}}{0}[/latex]
undefined
Simplify Expressions using the Properties of Identities, Inverses, and Zero
In the following exercises, simplify using the properties of identities, inverses, and zero.
[latex]19a+44 - 19a[/latex]
[latex]27c+16 - 27c[/latex]
16
[latex]38+11r - 38[/latex]
[latex]92+31s - 92[/latex]
31s
[latex]10\left(0.1d\right)[/latex]
[latex]100\left(0.01p\right)[/latex]
p
[latex]5\left(0.6q\right)[/latex]
[latex]40\left(0.05n\right)[/latex]
2n
[latex]\Large\frac{0}{r+20}[/latex] , where [latex]r\ne -20[/latex]
[latex]\Large\frac{0}{s+13}[/latex] , where [latex]s\ne -13[/latex]
0
[latex]\Large\frac{0}{u - 4.99}[/latex] , where [latex]u\ne 4.99[/latex]
[latex]\Large\frac{0}{v - 65.1}[/latex] , where [latex]v\ne 65.1[/latex]
0
[latex]0\div \left(x-\Large\frac{1}{2}\normalsize\right)[/latex] , where [latex]x\ne\Large\frac{1}{2}[/latex]
[latex]0\div \left(y-\Large\frac{1}{6}\normalsize\right)[/latex] , where [latex]y\ne\Large\frac{1}{6}[/latex]
0
[latex]\Large\frac{32 - 5a}{0}[/latex] , where [latex]32 - 5a\ne 0[/latex]
[latex]\Large\frac{28 - 9b}{0}[/latex] , where [latex]28 - 9b\ne 0[/latex]
undefined
[latex]\Large\frac{2.1+0.4c}{0}[/latex] , where [latex]2.1+0.4c\ne 0[/latex]
[latex]\Large\frac{1.75+9f}{0}[/latex] , where [latex]1.75+9f\ne 0[/latex]
undefined
[latex]\left(\Large\frac{3}{4}\normalsize +\Large\frac{9}{10}\normalsize m\right)\div 0[/latex] , where [latex]\Large\frac{3}{4}\normalsize +\Large\frac{9}{10}\normalsize m\ne 0[/latex]
[latex]\left(\Large\frac{5}{16}\normalsize n-\Large\frac{3}{7}\normalsize\right)\div 0[/latex] , where [latex]\Large\frac{5}{16}\normalsize n-\Large\frac{3}{7}\normalsize \ne 0[/latex]
undefined
[latex]\Large\frac{9}{10}\normalsize\cdot\Large\frac{10}{9}\normalsize\left(18p - 21\right)[/latex]
[latex]\Large\frac{5}{7}\normalsize\cdot\Large\frac{7}{5}\normalsize\left(20q - 35\right)[/latex]
20q − 35
[latex]15\cdot\Large\frac{3}{5}\normalsize\left(4d+10\right)[/latex]
[latex]18\cdot\Large\frac{5}{6}\normalsize\left(15h+24\right)[/latex]
225h + 360
EVERYDAY MATH
Insurance copayment
Carrie had to have [latex]5[/latex] fillings done. Each filling cost [latex]{$80}[/latex]. Her dental insurance required her to pay [latex]20%[/latex] of the cost. Calculate Carrie’s cost
ⓐ by finding her copay for each filling, then finding her total cost for [latex]5[/latex] fillings, and
ⓑ by multiplying [latex]5\left(0.20\right)\left(80\right)[/latex].
ⓒ Which of the Properties of Real Numbers did you use for part (b)?
Cooking time
Helen bought a [latex]\text{24-pound}[/latex] turkey for her family’s Thanksgiving dinner and wants to know what time to put the turkey in the oven. She wants to allow [latex]20[/latex] minutes per pound cooking time.
ⓐ Calculate the length of time needed to roast the turkey by multiplying [latex]24\cdot 20[/latex] to find the number of minutes and then multiplying the product by [latex]\Large\frac{1}{60}[/latex] to convert minutes into hours.
ⓑ Multiply [latex]24\left(20\cdot\Large\frac{1}{60}\normalsize\right)[/latex].
ⓒ Which of the Properties of Real Numbers allows you to multiply [latex]24\left(20\cdot\Large\frac{1}{60}\right)[/latex] instead of [latex]\left(24\cdot 20\right)\Large\frac{1}{60}[/latex]?
ⓐ 8 hours
ⓑ 8
ⓒ associative property of multiplication
WRITING EXERCISES
In your own words, describe the difference between the additive inverse and the multiplicative inverse of a number.
How can the use of the properties of real numbers make it easier to simplify expressions?
Answers will vary.
Determine Whether a Number is a Solution of an Equation
In the following exercises, determine whether each number is a solution of the given equation.
[latex]4x - 2=6[/latex]
ⓐ [latex]x=-2[/latex]
ⓑ [latex]x=-1[/latex]
ⓒ [latex]x=2[/latex]
- ⓐ no
- ⓑ yes
- ⓒ no
[latex]4y - 10=-14[/latex]
ⓐ [latex]y=-6[/latex]
ⓑ [latex]y=-1[/latex]
ⓒ [latex]y=1[/latex]
[latex]9a+27=-63[/latex]
ⓐ [latex]a=6[/latex]
ⓑ [latex]a=-6[/latex]
ⓒ [latex]a=-10[/latex]
- ⓐ no
- ⓑ no
- ⓒ yes
[latex]7c+42=-56[/latex]
ⓐ [latex]c=2[/latex]
ⓑ [latex]c=-2[/latex]
ⓒ [latex]c=-14[/latex]
Solve Equations Using the Addition and Subtraction Properties of Equality
In the following exercises, solve for the unknown.
[latex]n+12=5[/latex]
−7
[latex]m+16=2[/latex]
[latex]p+9=-8[/latex]
−17
[latex]q+5=-6[/latex]
[latex]u - 3=-7[/latex]
−4
[latex]v - 7=-8[/latex]
[latex]h - 10=-4[/latex]
6
[latex]k - 9=-5[/latex]
[latex]x+\left(-2\right)=-18[/latex]
−16
[latex]y+\left(-3\right)=-10[/latex]
[latex]r-\left(-5\right)=-9[/latex]
−14
[latex]s-\left(-2\right)=-11[/latex]
Model the Division Property of Equality
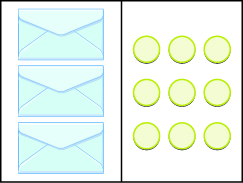
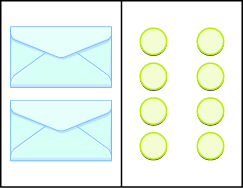
In the following exercises, write the equation modeled by the envelopes and counters and then solve it.
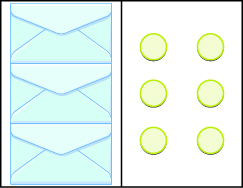
3x = 6; x = 2
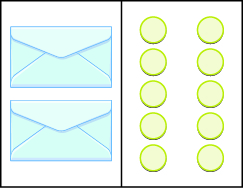
2x = 8; x = 4
Solve Equations Using the Division Property of Equality
In the following exercises, solve each equation using the division property of equality and check the solution.
[latex]5x=45[/latex]
9
[latex]4p=64[/latex]
[latex]-7c=56[/latex]
−8
[latex]-9x=54[/latex]
[latex]-14p=-42[/latex]
3
[latex]-8m=-40[/latex]
[latex]-120=10q[/latex]
−12
[latex]-75=15y[/latex]
[latex]24x=480[/latex]
20
[latex]18n=540[/latex]
[latex]-3z=0[/latex]
0
[latex]4u=0[/latex]
Translate to an Equation and Solve
In the following exercises, translate and solve.
Four more than [latex]n[/latex] is equal to 1.
n + 4 = 1; n = −3
Nine more than [latex]m[/latex] is equal to 5.
The sum of eight and [latex]p[/latex] is [latex]-3[/latex] .
8 + p = −3; p = −11
The sum of two and [latex]q[/latex] is [latex]-7[/latex] .
The difference of [latex]a[/latex] and three is [latex]-14[/latex] .
a − 3 = −14; a = −11
The difference of [latex]b[/latex] and [latex]5[/latex] is [latex]-2[/latex] .
The number −42 is the product of −7 and [latex]x[/latex] .
−42 = −7x; x = 6
The number −54 is the product of −9 and [latex]y[/latex] .
The product of [latex]f[/latex] and −15 is 75.
f(−15) = 75; f = 5
The product of [latex]g[/latex] and −18 is 36.
−6 plus [latex]c[/latex] is equal to 4.
−6 + c = 4; c = 10
−2 plus [latex]d[/latex] is equal to 1.
Nine less than [latex]n[/latex] is −4.
m − 9 = −4; m = 5
Thirteen less than [latex]n[/latex] is [latex]-10[/latex] .
Mixed Practice
In the following exercises, solve.
- ⓐ [latex]x+2=10[/latex]
- ⓑ [latex]2x=10[/latex]
- ⓐ 8
- ⓑ 5
- ⓐ [latex]y+6=12[/latex]
- ⓑ [latex]6y=12[/latex]
- ⓐ [latex]-3p=27[/latex]
- ⓑ [latex]p - 3=27[/latex]
- ⓐ −9
- ⓑ 30
- ⓐ [latex]-2q=34[/latex]
- ⓑ [latex]q - 2=34[/latex]
[latex]a - 4=16[/latex]
20
[latex]b - 1=11[/latex]
[latex]-8m=-56[/latex]
7
[latex]-6n=-48[/latex]
[latex]-39=u+13[/latex]
−52
[latex]-100=v+25[/latex]
[latex]11r=-99[/latex]
−9
[latex]15s=-300[/latex]
[latex]100=20d[/latex]
5
[latex]250=25n[/latex]
[latex]-49=x - 7[/latex]
−42
[latex]64=y - 4[/latex]
EVERYDAY MATH
Cookie packaging
A package of [latex]\text{51 cookies}[/latex] has [latex]3[/latex] equal rows of cookies. Find the number of cookies in each row, [latex]c[/latex], by solving the equation [latex]3c=51[/latex].
17 cookies
Kindergarten class
Connie’s kindergarten class has [latex]\text{24 children.}[/latex] She wants them to get into [latex]4[/latex] equal groups. Find the number of children in each group, [latex]g[/latex], by solving the equation [latex]4g=24[/latex].
WRITING EXERCISES
Is modeling the Division Property of Equality with envelopes and counters helpful to understanding how to solve the equation [latex]3x=15?[/latex] Explain why or why not.
Sample answer: It is helpful because it shows how the counters can be divided among the envelopes.
Suppose you are using envelopes and counters to model solving the equations [latex]x+4=12[/latex] and [latex]4x=12[/latex]. Explain how you would solve each equation.
Frida started to solve the equation [latex]-3x=36[/latex] by adding [latex]3[/latex] to both sides. Explain why Frida’s method will not solve the equation.
Sample answer: The operation used in the equation is multiplication. The inverse of multiplication is division, not addition.
Raoul started to solve the equation [latex]4y=40[/latex] by subtracting [latex]4[/latex] from both sides. Explain why Raoul’s method will not solve the equation.
Chapter Review Exercises
Introduction to integers
Locate Positive and Negative Numbers on the Number Line
In the following exercises, locate and label the integer on the number line.
[latex]5[/latex]

[latex]-5[/latex]
[latex]-3[/latex]

[latex]3[/latex]
[latex]-8[/latex]

[latex]-7[/latex]
Order Positive and Negative Numbers
In the following exercises, order each of the following pairs of numbers, using [latex]<[/latex]; or [latex]\text{>.}[/latex]
[latex]4\text{__}8[/latex]
<
[latex]-6\text{__}3[/latex]
[latex]-5\text{__}-10[/latex]
>
[latex]-9\text{__}-4[/latex]
[latex]2\text{__}-7[/latex]
>
[latex]-3\text{__}1[/latex]
Find Opposites
In the following exercises, find the opposite of each number.
[latex]6[/latex]
−6
[latex]-2[/latex]
[latex]-4[/latex]
4
[latex]3[/latex]
In the following exercises, simplify.
- ⓐ [latex]-\left(8\right)[/latex]
- ⓑ [latex]-\left(-8\right)[/latex]
- ⓐ −8
- ⓑ 8
- ⓐ [latex]-\left(9\right)[/latex]
- ⓑ [latex]-\left(-9\right)[/latex]
In the following exercises, evaluate.
[latex]-x,\text{when}[/latex]
ⓐ [latex]x=32[/latex]
ⓑ [latex]x=-32[/latex]
- ⓐ −32
- ⓑ 32
[latex]-n,\text{when}[/latex]
ⓐ [latex]n=20[/latex]
ⓐ [latex]n=-20[/latex]
ABSOLUTE VALUES
Simplify Absolute Values
In the following exercises, simplify.
[latex]|-21|[/latex]
21
[latex]|-42|[/latex]
[latex]|36|[/latex]
36
[latex]-|15|[/latex]
[latex]|0|[/latex]
0
[latex]-|-75|[/latex]
In the following exercises, evaluate.
[latex]|x|\text{when}x=-14[/latex]
14
[latex]-|r|\text{when}r=27[/latex]
[latex]-|-y|\text{when}y=33[/latex]
−33
[latex]|{\text{-n}}|\text{when}n=-4[/latex]
In the following exercises, fill in [latex]\text{<},\text{>},\text{or}=[/latex] for each of the following pairs of numbers.
[latex]-|-4|\text{__}4[/latex]
<
[latex]-2\text{__}|-2|[/latex]
[latex]-|-6|\text{__}-6[/latex]
=
[latex]-|-9|\text{__}|-9|[/latex]
In the following exercises, simplify.
[latex]-\left(-55\right)\text{and}-|-55|[/latex]
−55; −55
[latex]-\left(-48\right)\text{and}-|-48|[/latex]
[latex]|12 - 5|[/latex]
7
[latex]|9+7|[/latex]
[latex]6|-9|[/latex]
54
[latex]|14 - 8|-|-2|[/latex]
[latex]|9 - 3|-|5 - 12|[/latex]
−1
[latex]5+4|15 - 3|[/latex]
Translate Phrases to Expressions with Integers
In the following exercises, translate each of the following phrases into expressions with positive or negative numbers.
the opposite of [latex]16[/latex]
−16
the opposite of [latex]-8[/latex]
negative [latex]3[/latex]
−3
[latex]19[/latex] minus negative [latex]12[/latex]
a temperature of [latex]10[/latex] below zero
−10°
an elevation of [latex]\text{85 feet}[/latex] below sea level
Add Integers
Model Addition of Integers
In the following exercises, model the following to find the sum.
[latex]3+7[/latex]
10
[latex]-2+6[/latex]
[latex]5+\left(-4\right)[/latex]
1
[latex]-3+\left(-6\right)[/latex]
Simplify Expressions with Integers
In the following exercises, simplify each expression.
[latex]14+82[/latex]
96
[latex]-33+\left(-67\right)[/latex]
[latex]-75+25[/latex]
−50
[latex]54+\left(-28\right)[/latex]
[latex]11+\left(-15\right)+3[/latex]
−1
[latex]-19+\left(-42\right)+12[/latex]
[latex]-3+6\left(-1+5\right)[/latex]
21
[latex]10+4\left(-3+7\right)[/latex]
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
[latex]n+4\text{when}[/latex]
ⓐ [latex]n=-1[/latex]
ⓑ [latex]n=-20[/latex]
- ⓐ 3
- ⓑ −16
[latex]x+\left(-9\right)\text{when}[/latex]
ⓐ [latex]x=3[/latex]
ⓑ [latex]x=-3[/latex]
[latex]{\left(x+y\right)}^{3}\text{when}x=-4,y=1[/latex]
−27
[latex]{\left(u+v\right)}^{2}\text{when}u=-4,v=11[/latex]
TRANSLATE WORD PHRASES TO ALGEBRAIC EXPRESSIONS
In the following exercises, translate each phrase into an algebraic expression and then simplify.
[latex]\text{the sum of -8 and 2}[/latex]
−8 + 2 = −6
[latex]\text{4 more than -12}[/latex]
[latex]\text{10 more than the sum of -5 and -6}[/latex]
10 + [−5 + (−6)] = −1
[latex]\text{the sum of}3\text{and}-5,\text{increased by 18}[/latex]
Add Integers in Applications
In the following exercises, solve.
Temperature
On Monday, the high temperature in Denver was [latex]\text{-4 degrees.}[/latex] Tuesday’s high temperature was [latex]\text{20 degrees}[/latex] more. What was the high temperature on Tuesday?
16 degrees
Credit
Frida owed [latex]{$75}[/latex] on her credit card. Then she charged [latex]{$21}[/latex] more. What was her new balance?
Subtract Integers
Model Subtraction of Integers
In the following exercises, model the following.
[latex]6 - 1[/latex]

5
[latex]-4-\left(-3\right)[/latex]
[latex]2-\left(-5\right)[/latex]
7
[latex]-1 - 4[/latex]
Simplify Expressions with Integers
In the following exercises, simplify each expression.
[latex]24 - 16[/latex]
8
[latex]19-\left(-9\right)[/latex]
[latex]-31 - 7[/latex]
−38
[latex]-40-\left(-11\right)[/latex]
[latex]-52-\left(-17\right)-23[/latex]
−58
[latex]25-\left(-3 - 9\right)[/latex]
[latex]\left(1 - 7\right)-\left(3 - 8\right)[/latex]
−1
[latex]{3}^{2}-{7}^{2}[/latex]
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
[latex]x - 7\text{when}[/latex]
ⓐ [latex]x=5[/latex]
ⓑ [latex]x=-4[/latex]
- ⓐ −2
- ⓑ −11
[latex]10-y\text{when}[/latex]
ⓐ [latex]y=15[/latex]
ⓑ [latex]y=-16[/latex]
[latex]2{n}^{2}-n+5\text{when}n=-4[/latex]
41
[latex]-15 - 3{u}^{2}\text{when}u=-5[/latex]
Translate Phrases to Algebraic Expressions
In the following exercises, translate each phrase into an algebraic expression and then simplify.
the difference of [latex]-12\text{and}5[/latex]
−12 − 5 = −17
subtract [latex]23[/latex] from [latex]-50[/latex]
Subtract Integers in Applications
In the following exercises, solve the given applications.
Temperature
One morning the temperature in Bangor, Maine was [latex]\text{18 degrees.}[/latex] By afternoon, it had dropped [latex]\text{20 degrees.}[/latex] What was the afternoon temperature?
−2 degrees
Temperature
On January 4, the high temperature in Laredo, Texas was [latex]\text{78 degrees,}[/latex] and the high in Houlton, Maine was [latex]-28\text{degrees}[/latex]. What was the difference in temperature of Laredo and Houlton?
Multiply and Divide Integers
Multiply Integers
In the following exercises, multiply.
[latex]-9\cdot 4[/latex]
−36
[latex]5\left(-7\right)[/latex]
[latex]\left(-11\right)\left(-11\right)[/latex]
121
[latex]-1\cdot 6[/latex]
Divide Integers
In the following exercises, divide.
[latex]56\div \left(-8\right)[/latex]
−7
[latex]-120\div \left(-6\right)[/latex]
[latex]-96\div 12[/latex]
−8
[latex]96\div \left(-16\right)[/latex]
[latex]45\div \left(-1\right)[/latex]
−45
[latex]-162\div \left(-1\right)[/latex]
Simplify Expressions with Integers
In the following exercises, simplify each expression.
[latex]5\left(-9\right)-3\left(-12\right)[/latex]
−9
[latex]{\left(-2\right)}^{5}[/latex]
[latex]-{3}^{4}[/latex]
−81
[latex]\left(-3\right)\left(4\right)\left(-5\right)\left(-6\right)[/latex]
[latex]42 - 4\left(6 - 9\right)[/latex]
54
[latex]\left(8 - 15\right)\left(9 - 3\right)[/latex]
[latex]-2\left(-18\right)\div 9[/latex]
4
[latex]45\div \left(-3\right)-12[/latex]
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
[latex]7x - 3\text{when}x=-9[/latex]
−66
[latex]16 - 2n\text{when}n=-8[/latex]
[latex]5a+8b\text{when}a=-2,b=-6[/latex]
−58
[latex]{x}^{2}+5x+4\text{when}x=-3[/latex]
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate to an algebraic expression and simplify if possible.
the product of [latex]-12[/latex] and [latex]6[/latex]
−12(6) = −72
the quotient of [latex]3[/latex] and the sum of [latex]-7[/latex] and [latex]s[/latex]
Solve Equations using Integers; The Division Property of Equality
Determine Whether a Number is a Solution of an Equation
In the following exercises, determine whether each number is a solution of the given equation.
[latex]5x - 10=-35[/latex]
ⓐ [latex]x=-9[/latex]
ⓑ [latex]x=-5[/latex]
ⓒ [latex]x=5[/latex]
- ⓐ no
- ⓑ yes
- ⓒ no
[latex]8u+24=-32[/latex]
ⓐ [latex]u=-7[/latex]
ⓑ [latex]u=-1[/latex]
ⓒ [latex]u=7[/latex]
Using the Addition and Subtraction Properties of Equality
In the following exercises, solve.
[latex]a+14=2[/latex]
−12
[latex]b - 9=-15[/latex]
−6
[latex]c+\left(-10\right)=-17[/latex]
−7
[latex]d-\left(-6\right)=-26[/latex]
−32
Model the Division Property of Equality
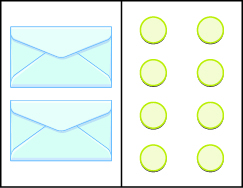
In the following exercises, write the equation modeled by the envelopes and counters. Then solve it.
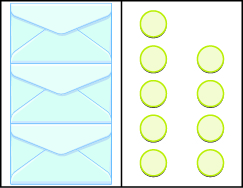
3x = 9; x = 3>
Solve Equations Using the Division Property of Equality
In the following exercises, solve each equation using the division property of equality and check the solution.
[latex]8p=72[/latex]
9
[latex]-12q=48[/latex]
[latex]-16r=-64[/latex]
4
[latex]-5s=-100[/latex]
Translate to an Equation and Solve.
In the following exercises, translate and solve.
[latex]\text{The product of -6 and}y\text{is}-42[/latex]
−6y = −42; y = 7
[latex]\text{The difference of}z\text{and -13 is -18.}[/latex]
Four more than [latex]m[/latex] is [latex]-48[/latex].
m + 4 = −48; m = −52
[latex]\text{The product of -21 and}n\text{is 63.}[/latex]
Everyday Math
Describe how you have used two topics from this chapter in your life outside of your math class during the past month.
Chapter Practice Test
Locate and label [latex]0,2,-4[/latex], and [latex]-1[/latex] on a number line.
In the following exercises, compare the numbers, using [latex]<\text{or}>\text{or}\text{=.}[/latex]
- ⓐ [latex]-6\text{__}3[/latex]
- ⓑ [latex]-1\text{__}-4[/latex]
- ⓐ <
- ⓑ >
- ⓐ [latex]-5\text{__}|-5|[/latex]
- ⓑ [latex]-|-2|\text{__}-2[/latex]
In the following exercises, find the opposite of each number.
- ⓐ [latex]-7[/latex]
- ⓑ [latex]8[/latex]
- ⓐ 7
- ⓑ −8
In the following exercises, simplify.
[latex]-\left(-22\right)[/latex]
[latex]|4 - 9|[/latex]
5
[latex]-8+6[/latex]
[latex]-15+\left(-12\right)[/latex]
−27
[latex]-7-\left(-3\right)[/latex]
[latex]10-\left(5 - 6\right)[/latex]
11
[latex]-3\cdot 8[/latex]
[latex]-6\left(-9\right)[/latex]
54
[latex]70\div \left(-7\right)[/latex]
[latex]{\left(-2\right)}^{3}[/latex]
−8
[latex]-{4}^{2}[/latex]
[latex]16 - 3\left(5 - 7\right)[/latex]
22
[latex]|21 - 6|-|-8|[/latex]
In the following exercises, evaluate.
[latex]35-a\text{when}a=-4[/latex]
39
[latex]{\left(-2r\right)}^{2}\text{when}r=3[/latex]
[latex]3m - 2n\text{when}m=6,n=-8[/latex]
34
[latex]-|-y|\text{when}y=17[/latex]
In the following exercises, translate each phrase into an algebraic expression and then simplify, if possible.
the difference of −7 and −4
−7 − (−4) = −3
the quotient of [latex]25[/latex] and the sum of [latex]m[/latex] and [latex]n[/latex].
In the following exercises, solve.
Early one morning, the temperature in Syracuse was [latex]-8\text{^\circ F.}[/latex] By noon, it had risen [latex]\text{12^\circ .}[/latex] What was the temperature at noon?
4°F
Collette owed [latex]{$128}[/latex] on her credit card. Then she charged [latex]{$65.}[/latex] What was her new balance?
In the following exercises, solve.
[latex]n+6=5[/latex]
n = −1
[latex]p - 11=-4[/latex]
[latex]-9r=-54[/latex]
r = 6
In the following exercises, translate and solve.
[latex]\text{The product of 15 and}x\text{is 75.}[/latex]
[latex]\text{Eight less than}y\text{is -32.}[/latex]
y − 8 = −32; y = −24
Candela Citations
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757
