Subtracting Fractions With Common Denominators

Learning Outcomes

  • Use fraction circles to find the difference between two fractions with like denominators
  • Subtract fractions with a like denominator without fraction circles
  • Subtract fractions with like denominators that contain variables

Model Fraction Subtraction

Subtracting two fractions with common denominators is much like adding fractions. Think of a pizza that was cut into [latex]12[/latex] slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or [latex]{\Large\frac{7}{12}}[/latex] of the pizza) left in the box. If Leonardo eats [latex]2[/latex] of these remaining pieces (or [latex]{\Large\frac{2}{12}}[/latex] of the pizza), how much is left? There would be [latex]5[/latex] pieces left (or [latex]{\Large\frac{5}{12}}[/latex] of the pizza).

[latex]{\Large\frac{7}{12}}-{\Large\frac{2}{12}}={\Large\frac{5}{12}}[/latex]

Let’s use fraction circles to model the same example, [latex]{\Large\frac{7}{12}}-{\Large\frac{2}{12}}[/latex].

Start with seven [latex]{\Large\frac{1}{12}}[/latex] pieces. Take away two [latex]{\Large\frac{1}{12}}[/latex] pieces. How many twelfths are left?

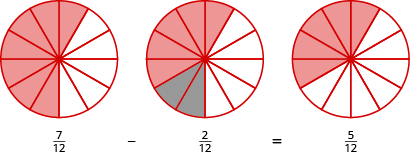
The bottom reads 7 twelfths minus 2 twelfths equals 5 twelfths. Above 7 twelfths, there is a circle divided into 12 equal pieces, with 7 pieces shaded in orange. Above 2 twelfths, the same circle is shown, but 2 of the 7 pieces are shaded in grey. Above 5 twelfths, the 2 grey pieces are no longer shaded, so there is a circle divided into 12 pieces with 5 of the pieces shaded in orange.
Again, we have five twelfths, [latex]{\Large\frac{5}{12}}[/latex].

Example

Use fraction circles to find the difference: [latex]{\Large\frac{4}{5}}-{\Large\frac{1}{5}}[/latex]

Solution:
Start with four [latex]{\Large\frac{1}{5}}[/latex] pieces. Take away one [latex]{\Large\frac{1}{5}}[/latex] piece. Count how many fifths are left. There are three [latex]{\Large\frac{1}{5}}[/latex] pieces left.

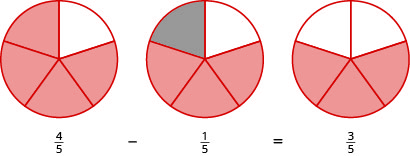
The bottom reads 4 fifths minus 1 fifth equals 3 fifths. Above 4 fifths, there is a circle divided into 5 equal pieces, with 4 pieces shaded in orange. Above 1 fifth, the same circle is shown, but 1 of the 4 shaded pieces is shaded in grey. Above 3 fifths, the 1 grey piece is no longer shaded, so there is a circle divided into 5 pieces with 3 of the pieces shaded in orange.

Try It

Subtract Fractions with a Common Denominator

We subtract fractions with a common denominator in much the same way as we add fractions with a common denominator.

Fraction Subtraction

If [latex]a,b,\text{ and }c[/latex] are numbers where [latex]c\ne 0[/latex], then

[latex]{\Large\frac{a}{c}}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}[/latex]

To subtract fractions with a common denominators, we subtract the numerators and place the difference over the common denominator.

Example

Find the difference: [latex]{\Large\frac{23}{24}}-{\Large\frac{14}{24}}[/latex]

Try It

Watch the following video for more examples of subtracting fractions with like denominators.

Example

Find the difference: [latex]{\Large\frac{y}{6}}-{\Large\frac{1}{6}}[/latex]

Try it

Example

Find the difference: [latex]{\Large-\frac{10}{x}-\frac{4}{x}}[/latex]

Try It

Now lets do an example that involves both addition and subtraction.

Example

Simplify: [latex]{\Large\frac{3}{8}}+\left(-{\Large\frac{5}{8}}\right)-{\Large\frac{1}{8}}[/latex]

Try It

In the next video we show more examples of subtracting fractions with a common denominator.  Make note of the second example, it addresses a common mistake made by students when simplifying fractions with variables.