Learning Outcomes
- Find the circumference and area of a circular object given it’s radius
- Find the circumference and area of a circular object given it’s diameter
- Calculate the diameter of a circular object given it’s circumference
Do you remember the properties of circles from Decimals and Fractions Together? We’ll show them here again to refer to as we use them to solve applications.
Properties of Circles
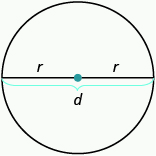
- [latex]r[/latex] is the length of the radius
- [latex]d[/latex] is the length of the diameter
- [latex]d=2r[/latex]
- Circumference is the perimeter of a circle. The formula for circumference is[latex]C=2\pi r[/latex]
- The formula for area of a circle is[latex]A=\pi {r}^{2}[/latex]
Remember, that we approximate [latex]\pi[/latex] with [latex]3.14[/latex] or [latex]\Large\frac{22}{7}[/latex] depending on whether the radius of the circle is given as a decimal or a fraction. If you use the [latex]\pi[/latex] key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the [latex]\pi[/latex] key uses more than two decimal places.
example
A circular sandbox has a radius of [latex]2.5[/latex] feet. Find the 1. circumference and 2. area of the sandbox.
Solution
| 1.
Step 1. Read the problem. Draw the figure and label it with the given information. |
 |
| Step 2. Identify what you are looking for. | the circumference of the circle |
| Step 3. Name. Choose a variable to represent it. | Let c = circumference of the circle |
| Step 4. Translate.
Write the appropriate formula Substitute |
[latex]C=2\pi r[/latex]
[latex]C=2\pi \left(2.5\right)[/latex] |
| Step 5. Solve the equation. | [latex]C\approx 2\left(3.14\right)\left(2.5\right)[/latex]
[latex]C\approx 15\text{ft}[/latex] |
| Step 6. Check. Does this answer make sense?
Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft (twice the radius), so its perimeter would be [latex]20[/latex] ft. This is slightly more than the circle’s circumference, [latex]15.7[/latex] ft.
|
|
| Step 7. Answer the question. | The circumference of the sandbox is [latex]15.7[/latex] feet. |
| 2.
Step 1. Read the problem. Draw the figure and label it with the given information. |
 |
| Step 2. Identify what you are looking for. | the area of the circle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area of the circle |
| Step 4. Translate.
Write the appropriate formula Substitute |
[latex]A=\pi {r}^{2}[/latex]
[latex]A=\pi{\left(2.5\right)}^{2}[/latex] |
| Step 5. Solve the equation. | [latex]A\approx \left(3.14\right){\left(2.5\right)}^{2}[/latex]
[latex]A\approx 19.625\text{sq. ft}[/latex] |
| Step 6. Check.
Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft, as shown in part ⓐ. So the area of the square would be [latex]25[/latex] sq. ft. This is slightly more than the circle’s area, [latex]19.625[/latex] sq. ft. |
|
| Step 7. Answer the question. | The area of the circle is [latex]19.625[/latex] square feet. |
try it
in the following video we show another example of how to find the area of a circle.
We usually see the formula for circumference in terms of the radius [latex]r[/latex] of the circle:
[latex]C=2\pi r[/latex]
But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms [latex]\text{of }d[/latex].
[latex]\begin{array}{cccc}& & & C=2\pi r\hfill \\ \text{Using the commutative property, we get}\hfill & & & C=\pi \cdot 2r\hfill \\ \text{Then substituting}d=2r\hfill & & & C=\pi \cdot d\hfill \\ \text{So}\hfill & & & C=\pi d\hfill \end{array}[/latex]
We will use this form of the circumference when we’re given the length of the diameter instead of the radius.
example
A circular table has a diameter of four feet. What is the circumference of the table?
try it
In the next video we show two more examples of how to find the circumference of a circle given it’s diameter, or it’s radius.
example
Find the diameter of a circle with a circumference of [latex]47.1[/latex] centimeters.
try it
Candela Citations
- Question ID 146787, 146786, 146785. Authored by: Lumen Learning. License: CC BY: Attribution
- Examples: Determine the Circumference of a Circle. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/sHtsnC2Mgnk. License: CC BY: Attribution
- Example: Determine the Area of a Circle. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/SIKkWLqt2mQ. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757




