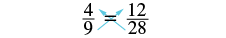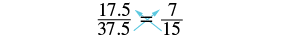Learning Outcomes
- Given a statement, write a proportion
- Given an equation, determine whether it is a proportion
In the section on Ratios and Rates we saw some ways they are used in our daily lives. When two ratios or rates are equal, the equation relating them is called a proportion.
Proportion
A proportion is an equation of the form [latex]{\Large\frac{a}{b}}={\Large\frac{c}{d}}[/latex], where [latex]b\ne 0,d\ne 0[/latex].
The proportion states two ratios or rates are equal. The proportion is read [latex]\text{"}a[/latex] is to [latex]b[/latex], as [latex]c[/latex] is to [latex]d\text{".}[/latex]
The equation [latex]{\Large\frac{1}{2}}={\Large\frac{4}{8}}[/latex] is a proportion because the two fractions are equal. The proportion [latex]{\Large\frac{1}{2}}={\Large\frac{4}{8}}[/latex] is read “[latex]1[/latex] is to [latex]2[/latex] as [latex]4[/latex] is to [latex]8[/latex]“.
If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion [latex]{\Large\frac{\text{20 students}}{\text{1 teacher}}}={\Large\frac{\text{60 students}}{\text{3 teachers}}}[/latex] we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.
example
Write each sentence as a proportion:
1. [latex]3[/latex] is to [latex]7[/latex] as [latex]15[/latex] is to [latex]35[/latex].
2. [latex]5[/latex] hits in [latex]8[/latex] at bats is the same as [latex]30[/latex] hits in [latex]48[/latex] at-bats.
3. [latex]\text{\$1.50}[/latex] for [latex]6[/latex] ounces is equivalent to [latex]\text{\$2.25}[/latex] for [latex]9[/latex] ounces.
Solution
| 1. | |
| [latex]3[/latex] is to [latex]7[/latex] as [latex]15[/latex] is to [latex]35[/latex]. | |
| Write as a proportion. | [latex]{\Large\frac{3}{7}}={\Large\frac{15}{35}}[/latex] |
| 2. | |
| [latex]5[/latex] hits in [latex]8[/latex] at-bats is the same as [latex]30[/latex] hits in [latex]48[/latex] at-bats. | |
| Write each fraction to compare hits to at-bats. | [latex]{\Large\frac{\text{hits}}{\text{at-bats}}}={\Large\frac{\text{hits}}{\text{at-bats}}}[/latex] |
| Write as a proportion. | [latex]{\Large\frac{5}{8}}={\Large\frac{30}{48}}[/latex] |
| 3. | |
| [latex]\text{\$1.50}[/latex] for [latex]6[/latex] ounces is equivalent to [latex]\text{\$2.25}[/latex] for [latex]9[/latex] ounces. | |
| Write each fraction to compare dollars to ounces. | [latex]{\Large\frac{$}{\text{ounces}}}={\Large\frac{$}{\text{ounces}}}[/latex] |
| Write as a proportion. | [latex]{\Large\frac{1.50}{6}}={\Large\frac{2.25}{9}}[/latex] |
try it
Look at the proportions [latex]{\Large\frac{1}{2}}={\Large\frac{4}{8}}[/latex] and [latex]{\Large\frac{2}{3}}={\Large\frac{6}{9}}[/latex]. From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?
To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross products because of the cross formed. The cross products of a proportion are equal.

Cross Products of a Proportion
For any proportion of the form [latex]{\Large\frac{a}{b}}={\Large\frac{c}{d}}[/latex], where [latex]b\ne 0,d\ne 0[/latex], its cross products are equal.

Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are the equal, we have a proportion.
example
Determine whether each equation is a proportion:
1. [latex]{\Large\frac{4}{9}}={\Large\frac{12}{28}}[/latex]
2. [latex]{\Large\frac{17.5}{37.5}}={\Large\frac{7}{15}}[/latex]
try it
Candela Citations
- Question ID 146809, 146808, 146807. Authored by: Lumen Learning. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757