Exponential Growth and Decay

In real-world applications, we need to model the behavior of a function. In mathematical modeling, we choose a familiar general function with properties that suggest that it will model the real-world phenomenon we wish to analyze. In the case of rapid growth, we may choose the exponential growth function:

[latex]y={A}_{0}{e}^{kt}[/latex]

where [latex]{A}_{0}[/latex] is equal to the value at time zero, e is Euler’s constant, and k is a positive constant that determines the rate (percentage) of growth. We may use the exponential growth function in applications involving doubling time, the time it takes for a quantity to double. Such phenomena as wildlife populations, financial investments, biological samples, and natural resources may exhibit growth based on a doubling time. In some applications, however, as we will see when we discuss the logistic equation, the logistic model sometimes fits the data better than the exponential model.

On the other hand, if a quantity is falling rapidly toward zero, without ever reaching zero, then we should probably choose the exponential decay model. Again, we have the form [latex]y={A}_{0}{e}^{-kt}[/latex] where [latex]{A}_{0}[/latex] is the starting value, and e is Euler’s constant. Now k is a negative constant that determines the rate of decay. We may use the exponential decay model when we are calculating half-life, or the time it takes for a substance to exponentially decay to half of its original quantity. We use half-life in applications involving radioactive isotopes.

In our choice of a function to serve as a mathematical model, we often use data points gathered by careful observation and measurement to construct points on a graph and hope we can recognize the shape of the graph. Exponential growth and decay graphs have a distinctive shape, as we can see in the graphs below. It is important to remember that, although parts of each of the two graphs seem to lie on the x-axis, they are really a tiny distance above the x-axis.

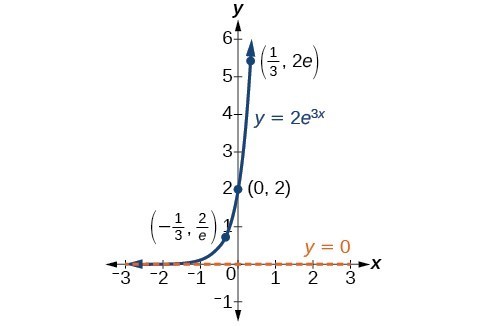
A graph showing exponential growth. The equation is [latex]y=2{e}^{3x}[/latex].

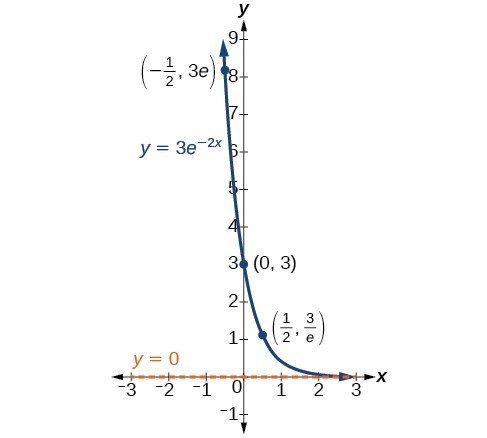
A graph showing exponential decay. The equation is [latex]y=3{e}^{-2x}[/latex].

Exponential growth and decay often involve very large or very small numbers. To describe these numbers, we often use orders of magnitude. The order of magnitude is the power of ten when the number is expressed in scientific notation with one digit to the left of the decimal. For example, the distance to the nearest star, Proxima Centauri, measured in kilometers, is 40,113,497,200,000 kilometers. Expressed in scientific notation, this is [latex]4.01134972\times {10}^{13}[/latex]. We could describe this number as having order of magnitude [latex]{10}^{13}[/latex].

Try It

The graphs below include important characteristics of an exponential function that can illustrate whether the function represents growth or decay and the speed at which the function grows or decays.

Your task is to add the key features from the graphs above to graph made using an online graphing calculator and adjusting the [latex]a[/latex] and [latex]k[/latex] values. The function [latex]f(x) = a\cdot{e}^{kx}[/latex] will be what you use as your starting point.

Include the following key features:

• The horizontal asymptote
• y-intercept
• The key points labeled in the still graphs above

Show Solution

Below is what the graph would look like in Desmos, but you can use any online graphing tool.

Example: Graphing Exponential Growth

A population of bacteria doubles every hour. If the culture started with 10 bacteria, graph the population as a function of time.

Show Solution

When an amount grows at a fixed percent per unit time, the growth is exponential. To find [latex]{A}_{0}[/latex] we use the fact that [latex]{A}_{0}[/latex] is the amount at time zero, so [latex]{A}_{0}=10[/latex]. To find k, use the fact that after one hour [latex]\left(t=1\right)[/latex] the population doubles from 10 to 20. The formula is derived as follows:

[latex]\begin{array}{l}\text{ }20=10{e}^{k\cdot 1}\hfill & \hfill \\ \text{ }2={e}^{k}\hfill & \text{Divide both sides by 10}\hfill \\ \mathrm{ln}2=k\hfill & \text{Take the natural logarithm of both sides}\hfill \end{array}[/latex]

so [latex]k=\mathrm{ln}\left(2\right)[/latex]. Thus the equation we want to graph is [latex]y=10{e}^{\left(\mathrm{ln}2\right)t}=10{\left({e}^{\mathrm{ln}2}\right)}^{t}=10\cdot {2}^{t}[/latex]. The graph is shown below.

The graph of [latex]y=10{e}^{\left(\mathrm{ln}2\right)t}[/latex].

Analysis of the Solution

The population of bacteria after ten hours is 10,240. We could describe this amount as being of the order of magnitude [latex]{10}^{4}[/latex]. The population of bacteria after twenty hours is 10,485,760 which is of the order of magnitude [latex]{10}^{7}[/latex], so we could say that the population has increased by three orders of magnitude in ten hours.

Calculating Doubling Time

For growing quantities, we might want to find out how long it takes for a quantity to double. As we mentioned above, the time it takes for a quantity to double is called the doubling time.

Given the basic exponential growth equation [latex]A={A}_{0}{e}^{kt}[/latex], doubling time can be found by solving for when the original quantity has doubled, that is, by solving [latex]2{A}_{0}={A}_{0}{e}^{kt}[/latex].

The formula is derived as follows:

[latex]\begin{array}{l}2{A}_{0}={A}_{0}{e}^{kt}\hfill & \hfill \\ 2={e}^{kt}\hfill & \text{Divide both sides by }{A}_{0}.\hfill \\ \mathrm{ln}2=kt\hfill & \text{Take the natural logarithm of both sides}.\hfill \\ t=\frac{\mathrm{ln}2}{k}\hfill & \text{Divide by the coefficient of }t.\hfill \end{array}[/latex]

Thus the doubling time is

[latex]t=\frac{\mathrm{ln}2}{k}[/latex]

Half-Life

We now turn to exponential decay. One of the common terms associated with exponential decay, as stated above, is half-life, the length of time it takes an exponentially decaying quantity to decrease to half its original amount. Every radioactive isotope has a half-life, and the process describing the exponential decay of an isotope is called radioactive decay.

To find the half-life of a function describing exponential decay, solve the following equation:

[latex]\frac{1}{2}{A}_{0}={A}_{o}{e}^{kt}[/latex]

We find that the half-life depends only on the constant k and not on the starting quantity [latex]{A}_{0}[/latex].

The formula is derived as follows

[latex]\begin{array}{l}\frac{1}{2}{A}_{0}={A}_{o}{e}^{kt}\hfill & \hfill \\ \frac{1}{2}={e}^{kt}\hfill & \text{Divide both sides by }{A}_{0}.\hfill \\ \mathrm{ln}\left(\frac{1}{2}\right)=kt\hfill & \text{Take the natural log of both sides}.\hfill \\ -\mathrm{ln}\left(2\right)=kt\hfill & \text{Apply properties of logarithms}.\hfill \\ -\frac{\mathrm{ln}\left(2\right)}{k}=t\hfill & \text{Divide by }k.\hfill \end{array}[/latex]

Since t, the time, is positive, k must, as expected, be negative. This gives us the half-life formula

[latex]t=-\frac{\mathrm{ln}\left(2\right)}{k}[/latex]

In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.

One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life. The table below lists the half-life for several of the more common radioactive substances.

We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:

[latex]\begin{array}{l}A\left(t\right)={A}_{0}{e}^{\frac{\mathrm{ln}\left(0.5\right)}{T}t}\hfill \\ A\left(t\right)={A}_{0}{e}^{\mathrm{ln}\left(0.5\right)\frac{t}{T}}\hfill \\ A\left(t\right)={A}_{0}{\left({e}^{\mathrm{ln}\left(0.5\right)}\right)}^{\frac{t}{T}}\hfill \\ A\left(t\right)={A}_{0}{\left(\frac{1}{2}\right)}^{\frac{t}{T}}\hfill \end{array}[/latex]

where

• [latex]{A}_{0}[/latex] is the amount initially present
• [latex]T[/latex] is the half-life of the substance
• [latex]t[/latex] is the time period over which the substance is studied
• [latex]A[/latex], or [latex]A(t)[/latex], is the amount of the substance present after time [latex]t[/latex]

Radiocarbon Dating

The formula for radioactive decay is important in radiocarbon dating which is used to calculate the approximate date a plant or animal died. Radiocarbon dating was discovered in 1949 by Willard Libby who won a Nobel Prize for his discovery. It compares the difference between the ratio of two isotopes of carbon in an organic artifact or fossil to the ratio of those two isotopes in the air. It is believed to be accurate to within about 1% error for plants or animals that died within the last 60,000 years.

Carbon-14 is a radioactive isotope of carbon that has a half-life of 5,730 years. It occurs in small quantities in the carbon dioxide in the air we breathe. Most of the carbon on Earth is carbon-12 which has an atomic weight of 12 and is not radioactive. Scientists have determined the ratio of carbon-14 to carbon-12 in the air for the last 60,000 years using tree rings and other organic samples of known dates—although the ratio has changed slightly over the centuries.

As long as a plant or animal is alive, the ratio of the two isotopes of carbon in its body is close to the ratio in the atmosphere. When it dies, the carbon-14 in its body decays and is not replaced. By comparing the ratio of carbon-14 to carbon-12 in a decaying sample to the known ratio in the atmosphere, the date the plant or animal died can be approximated.

Since the half-life of carbon-14 is 5,730 years, the formula for the amount of carbon-14 remaining after t years is

[latex]A\approx {A}_{0}{e}^{\left(\frac{\mathrm{ln}\left(0.5\right)}{5730}\right)t}[/latex]

where

• [latex]A[/latex] is the amount of carbon-14 remaining
• [latex]{A}_{0}[/latex] is the amount of carbon-14 when the plant or animal began decaying.

This formula is derived as follows:

[latex]\begin{array}{l}\text{ }A={A}_{0}{e}^{kt}\hfill & \text{The continuous growth formula}.\hfill \\ \text{ }0.5{A}_{0}={A}_{0}{e}^{k\cdot 5730}\hfill & \text{Substitute the half-life for }t\text{ and }0.5{A}_{0}\text{ for }f\left(t\right).\hfill \\ \text{ }0.5={e}^{5730k}\hfill & \text{Divide both sides by }{A}_{0}.\hfill \\ \mathrm{ln}\left(0.5\right)=5730k\hfill & \text{Take the natural log of both sides}.\hfill \\ \text{ }k=\frac{\mathrm{ln}\left(0.5\right)}{5730}\hfill & \text{Divide both sides by the coefficient of }k.\hfill \\ \text{ }A={A}_{0}{e}^{\left(\frac{\mathrm{ln}\left(0.5\right)}{5730}\right)t}\hfill & \text{Substitute for }r\text{ in the continuous growth formula}.\hfill \end{array}[/latex]

To find the age of an object we solve this equation for t:

[latex]t=\frac{\mathrm{ln}\left(\frac{A}{{A}_{0}}\right)}{-0.000121}[/latex]

Out of necessity, we neglect here the many details that a scientist takes into consideration when doing carbon-14 dating, and we only look at the basic formula. The ratio of carbon-14 to carbon-12 in the atmosphere is approximately 0.0000000001%. Let r be the ratio of carbon-14 to carbon-12 in the organic artifact or fossil to be dated determined by a method called liquid scintillation. From the equation [latex]A\approx {A}_{0}{e}^{-0.000121t}[/latex] we know the ratio of the percentage of carbon-14 in the object we are dating to the percentage of carbon-14 in the atmosphere is [latex]r=\frac{A}{{A}_{0}}\approx {e}^{-0.000121t}[/latex]. We solve this equation for t, to get

[latex]t=\frac{\mathrm{ln}\left(r\right)}{-0.000121}[/latex]