Union, Intersection, and Complement

Learning Outcomes

  • Perform the operations of union, intersection, complement, and difference on sets using proper notation.
  • Be able to draw and interpret Venn diagrams of set relations and operations.

Commonly, sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.

Math vocabulary and notation

It takes repetition and practice to obtain new vocabulary in a language that is new to you. Math is no different in many respects than learning a new language, with all its vocabulary, syntax, and spelling conventions. The symbols in this section may be completely unfamiliar to you. If so, you’ll need to spend time with them, employing flashcards and writing them out by hand in context.

Give yourself time to learn and appreciate the language of mathematics!

Union, Intersection, and Complement

The union of two sets contains all the elements contained in either set (or both sets). The union is notated A ⋃ B. More formally, x ∊ A ⋃ B if x ∈ A or x ∈ B (or both)

The intersection of two sets contains only the elements that are in both sets. The intersection is notated A ⋂ B. More formally, x ∈ A ⋂ B if x ∈ A and x ∈ B.

The complement of a set A contains everything that is not in the set A. The complement is notated A’, or Ac, or sometimes ~A.

A universal set is a set that contains all the elements we are interested in. This would have to be defined by the context.

A complement is relative to the universal set, so Ac contains all the elements in the universal set that are not in A.

a new use for a superscript

Notice in the descriptions of the notation introduced above that the complement of a set is denoted [latex]A^{c}[/latex]. This superscript is not an exponent. It is a decoration that denotes the complement of a set.

 

Example

  1. If we were discussing searching for books, the universal set might be all the books in the library.
  2. If we were grouping your Facebook friends, the universal set would be all your Facebook friends.
  3. If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers

Example

Suppose the universal set is U = all whole numbers from 1 to 9. If A = {1, 2, 4}, then Ac = {3, 5, 6, 7, 8, 9}.

Try It

intersection and union symbols

The intersection [latex]\cup[/latex] and union [latex]\cap[/latex] symbols look a little like letters in the alphabet. In fact, that’s a trick for remembering them.

The union symbol looks like a capital U, for union.

The intersection symbol looks a little like a big lower-case n, for in-tersect

 

Example

Consider the sets:

A = {red, green, blue}
B = {red, yellow, orange}
C = {red, orange, yellow, green, blue, purple}

Find the following:

  1. Find A ⋃ B
  2. Find A ⋂ B
  3. Find Ac⋂ C

Try It

Notice that in the example above, it would be hard to just ask for Ac, since everything from the color fuchsia to puppies and peanut butter are included in the complement of the set. For this reason, complements are usually only used with intersections, or when we have a universal set in place.

As we saw earlier with the expression Ac ⋂ C, set operations can be grouped together. Grouping symbols can be used like they are with arithmetic – to force an order of operations.

 

Example

Suppose H = {cat, dog, rabbit, mouse}, F = {dog, cow, duck, pig, rabbit}, and W = {duck, rabbit, deer, frog, mouse}

  1. Find (H ⋂ F) ⋃ W
  2. Find H ⋂ (F ⋃ W)
  3. Find (H ⋂ F)c ⋂ W

Venn Diagrams

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18th century. These illustrations now called Venn Diagrams.

Venn Diagram

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets.

Basic Venn diagrams can illustrate the interaction of two or three sets.

Example

Create Venn diagrams to illustrate A ⋃ B, A ⋂ B, and Ac ⋂ B

A ⋃ B contains all elements in either set.

Example

Use a Venn diagram to illustrate (H ⋂ F)c ⋂ W

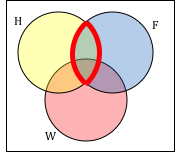
Example

Create an expression to represent the outlined part of the Venn diagram shown.

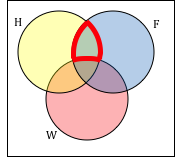
A venn diagram representing three sets (H, F, W) with overlapping sections. The portion outlined in red represents H intersect F intersect W complement.

Try It

Create an expression to represent the outlined portion of the Venn diagram shown.

A venn diagram with three overlapping sets (A, B, and C). The region representing A union B intersect C complement is outlined in red.