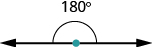
Are you familiar with the phrase ‘do a [latex]180[/latex]?’ It means to make a full turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is [latex]180[/latex] degrees. See the image below.

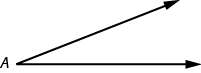
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex. An angle is named by its vertex. In the image below, [latex]\angle A[/latex] is the angle with vertex at point [latex]A[/latex]. The measure of [latex]\angle A[/latex] is written [latex]m\angle A[/latex].

We measure angles in degrees, and use the symbol [latex]^ \circ[/latex] to represent degrees. We use the abbreviation [latex]m[/latex] to for the measure of an angle. So if [latex]\angle A[/latex] is [latex]\text{27}^ \circ[/latex], we would write [latex]m\angle A=27^ \circ[/latex].

We classify angles based on their measures.  The four types of angles are acute, right, obtuse, and straight.  An acute angle is an angle that measures between [latex]\text{0}^ \circ[/latex] and [latex]\text{90}^ \circ[/latex].  A right angle measures exactly [latex]\text{90}^ \circ[/latex]. An obtuse angle measures between [latex]\text{90}^ \circ[/latex] and [latex]\text{180}^ \circ[/latex].  A straight angle measures exactly [latex]\text{180}^ \circ[/latex].

Supplementary and Complementary Angles

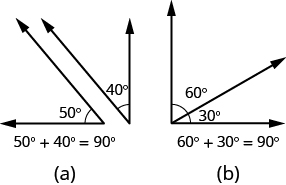
If the sum of the measures of two angles is [latex]\text{180}^ \circ[/latex], then they are called supplementary angles. In the images below, each pair of angles is supplementary because their measures add to [latex]\text{180}^ \circ[/latex]. Each angle is the supplement of the other.

The sum of the measures of supplementary angles is [latex]\text{180}^ \circ[/latex].

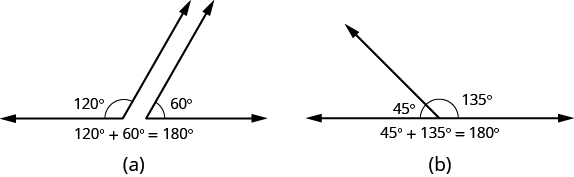
If the sum of the measures of two angles is [latex]\text{90}^ \circ[/latex], then the angles are complementary angles. In the images below, each pair of angles is complementary, because their measures add to [latex]\text{90}^ \circ[/latex]. Each angle is the complement of the other.

The sum of the measures of complementary angles is [latex]\text{90}^ \circ[/latex].

In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.

In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.

The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.

example

An angle measures [latex]\text{40}^ \circ[/latex].

1. Find its supplement

2. Find its complement

Solution

1.
Step 1. Read the problem. Draw the figure and label it with the given information.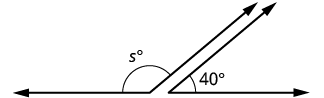
Step 2. Identify what you are looking for.	The supplement of a [latex]40°[/latex]angle.
Step 3. Name. Choose a variable to represent it.	Let [latex]s=[/latex]the measure of the supplement.
Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information.	[latex]m\angle A+m\angle B=180°[/latex] [latex]s+40°=180°[/latex]
Step 5. Solve the equation.	[latex]s=140°[/latex]
Step 6. Check: [latex]140°+40°\stackrel{?}{=}180°[/latex] [latex]180°=180°\checkmark[/latex]
Step 7. Answer the question.	The supplement of the [latex]40°[/latex]angle is [latex]140°[/latex].

2.
Step 1. Read the problem. Draw the figure and label it with the given information.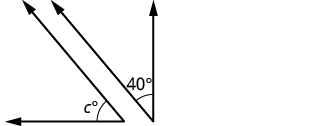
Step 2. Identify what you are looking for.	The complement of a [latex]40°[/latex]angle.
Step 3. Name. Choose a variable to represent it.	Let [latex]c=[/latex]the measure of the complement.
Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information.	[latex]m\angle A+m\angle B=90°[/latex]
Step 5. Solve the equation.	[latex]c+40°=90°[/latex] [latex]c=50°[/latex]
Step 6. Check: [latex]50°+40°\stackrel{?}{=}90°[/latex] [latex]90°=90°\quad\checkmark[/latex]
Step 7. Answer the question.	The complement of the [latex]40°[/latex]angle is [latex]50°[/latex].

In the following video we show more examples of how to find the supplement and complement of an angle.

Did you notice that the words complementary and supplementary are in alphabetical order just like [latex]90[/latex] and [latex]180[/latex] are in numerical order?

Exercises

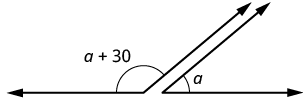
Two angles are supplementary. The larger angle is [latex]\text{30}^ \circ[/latex] more than the smaller angle. Find the measure of both angles.

Show Solution

Solution:

Step 1. Read the problem. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.	The measures of both angles.
Step 3. Name. Choose a variable to represent it. The larger angle is 30° more than the smaller angle.	Let [latex]a=[/latex] measure of smaller angle [latex]a+30=[/latex] measure of larger angle
Step 4. Translate. Write the appropriate formula and substitute.	[latex]m\angle A+m\angle B=180[/latex]
Step 5. Solve the equation.	[latex](a+30)+a=180[/latex] [latex]2a+30=180[/latex] [latex]2a=150[/latex] [latex]a=75=[/latex] measure of smaller angle. [latex]a+30=[/latex] measure of larger angle. [latex]75+30[/latex] [latex]105[/latex]
Step 6. Check: [latex]m\angle A+m\angle B=180°[/latex] [latex]75°+105°\stackrel{?}{=}180°[/latex] [latex]180°=180°\quad\checkmark[/latex]
Step 7. Answer the question.	The measures of the angle are [latex]75°[/latex]and [latex]105°[/latex].