Write the equation for a linear function from the graph of a line

Recall that in Linear Functions, we wrote the equation for a linear function from a graph. Now we can extend what we know about graphing linear functions to analyze graphs a little more closely. Begin by taking a look at Figure 8. We can see right away that the graph crosses the y-axis at the point (0, 4) so this is the y-intercept.

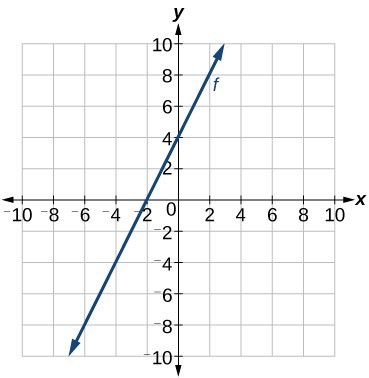
Figure 8

Then we can calculate the slope by finding the rise and run. We can choose any two points, but let’s look at the point (–2, 0). To get from this point to the y-intercept, we must move up 4 units (rise) and to the right 2 units (run). So the slope must be

[latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{2}=2[/latex]

Substituting the slope and y-intercept into the slope-intercept form of a line gives

[latex]y=2x+4[/latex]

How To: Given a graph of linear function, find the equation to describe the function.

  1. Identify the y-intercept of an equation.
  2. Choose two points to determine the slope.
  3. Substitute the y-intercept and slope into the slope-intercept form of a line.

Example 4: Matching Linear Functions to Their Graphs

Match each equation of the linear functions with one of the lines in Figure 9.

  1. [latex]f\left(x\right)=2x+3[/latex]
  2. [latex]g\left(x\right)=2x - 3[/latex]
  3. [latex]h\left(x\right)=-2x+3[/latex]
  4. [latex]j\left(x\right)=\frac{1}{2}x+3[/latex]
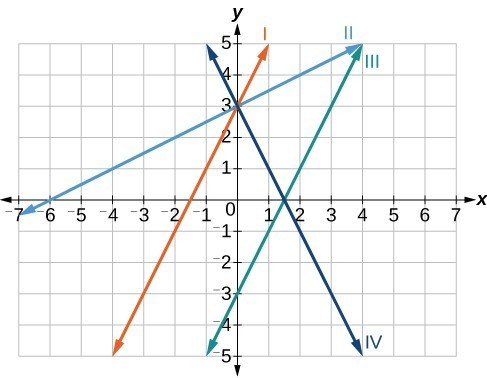
Graph of three lines, line 1) passes through (0,3) and (-2, -1), line 2) passes through (0,3) and (-6,0), line 3) passes through (0,-3) and (2,1)

Figure 9

Solution

Analyze the information for each function.

  1. This function has a slope of 2 and a y-intercept of 3. It must pass through the point (0, 3) and slant upward from left to right. We can use two points to find the slope, or we can compare it with the other functions listed. Function g has the same slope, but a different y-intercept. Lines I and III have the same slant because they have the same slope. Line III does not pass through (0, 3) so f must be represented by line I.
  2. This function also has a slope of 2, but a y-intercept of –3. It must pass through the point (0, –3) and slant upward from left to right. It must be represented by line III.
  3. This function has a slope of –2 and a y-intercept of 3. This is the only function listed with a negative slope, so it must be represented by line IV because it slants downward from left to right.
  4. This function has a slope of [latex]\frac{1}{2}[/latex] and a y-intercept of 3. It must pass through the point (0, 3) and slant upward from left to right. Lines I and II pass through (0, 3), but the slope of j is less than the slope of f so the line for j must be flatter. This function is represented by Line II.

Now we can re-label the lines as in Figure 10.

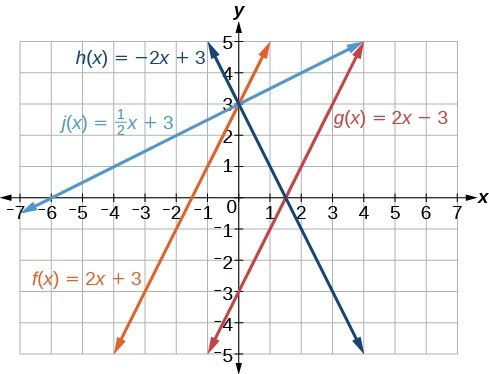
Figure 10

Finding the x-intercept of a Line

So far, we have been finding the y-intercepts of a function: the point at which the graph of the function crosses the y-axis. A function may also have an x-intercept, which is the x-coordinate of the point where the graph of the function crosses the x-axis. In other words, it is the input value when the output value is zero.

To find the x-intercept, set a function f(x) equal to zero and solve for the value of x. For example, consider the function shown.

[latex]f\left(x\right)=3x - 6[/latex]

Set the function equal to 0 and solve for x.

[latex]\begin{cases}0=3x - 6\hfill \\ 6=3x\hfill \\ 2=x\hfill \\ x=2\hfill \end{cases}[/latex]

The graph of the function crosses the x-axis at the point (2, 0).

Q & A

Do all linear functions have x-intercepts?

No. However, linear functions of the form y = c, where c is a nonzero real number are the only examples of linear functions with no x-intercept. For example, y = 5 is a horizontal line 5 units above the x-axis. This function has no x-intercepts.


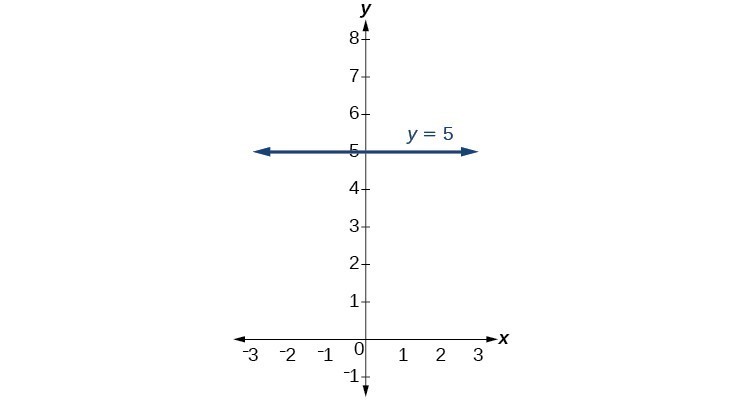
Graph of y = 5.

Figure 11

A General Note: x-intercept

The x-intercept of the function is value of x when f(x) = 0. It can be solved by the equation 0 = mx + b.

Example 5: Finding an x-intercept

Find the x-intercept of [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex].

Solution

Set the function equal to zero to solve for x.

[latex]\begin{cases}0=\frac{1}{2}x - 3\\ 3=\frac{1}{2}x\\ 6=x\\ x=6\end{cases}[/latex]

The graph crosses the x-axis at the point (6, 0).

Analysis of the Solution

A graph of the function is shown in Figure 12. We can see that the x-intercept is (6, 0) as we expected.

Figure 12. The graph of the linear function [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex].

Try It 4

Find the x-intercept of [latex]f\left(x\right)=\frac{1}{4}x - 4[/latex].

Solution

Describing Horizontal and Vertical Lines

There are two special cases of lines on a graph—horizontal and vertical lines. A horizontal line indicates a constant output, or y-value. In Figure 13, we see that the output has a value of 2 for every input value. The change in outputs between any two points, therefore, is 0. In the slope formula, the numerator is 0, so the slope is 0. If we use m = 0 in the equation [latex]f\left(x\right)=mx+b[/latex], the equation simplifies to [latex]f\left(x\right)=b[/latex]. In other words, the value of the function is a constant. This graph represents the function [latex]f\left(x\right)=2[/latex].

Figure 13. A horizontal line representing the function [latex]f\left(x\right)=2[/latex].

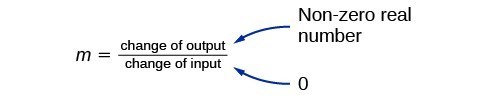
M equals change of output divided by change of input. The numerator is a non-zero real number, and the change of input is zero.

Figure 14

A vertical line indicates a constant input, or x-value. We can see that the input value for every point on the line is 2, but the output value varies. Because this input value is mapped to more than one output value, a vertical line does not represent a function. Notice that between any two points, the change in the input values is zero. In the slope formula, the denominator will be zero, so the slope of a vertical line is undefined.

Notice that a vertical line, such as the one in Figure 15, has an x-intercept, but no y-intercept unless it’s the line x = 0. This graph represents the line x = 2.

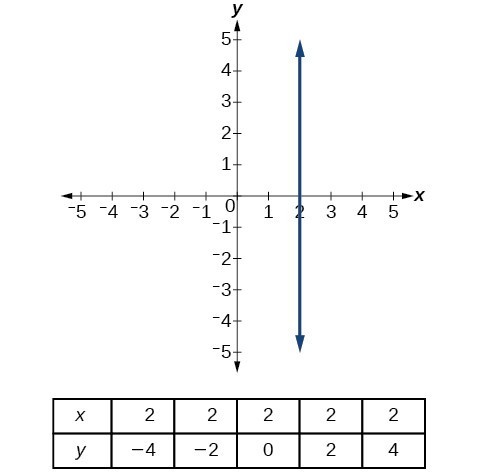
Figure 15. The vertical line, x = 2, which does not represent a function.

A General Note: Horizontal and Vertical Lines

Lines can be horizontal or vertical.

A horizontal line is a line defined by an equation in the form [latex]f\left(x\right)=b[/latex].

A vertical line is a line defined by an equation in the form [latex]x=a[/latex].

Example 6: Writing the Equation of a Horizontal Line

Write the equation of the line graphed in Figure 16.

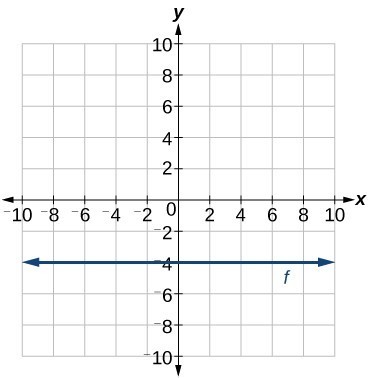
Graph of x = 7.

Figure 16

Solution

For any x-value, the y-value is –4, so the equation is y = –4.

Example 7: Writing the Equation of a Vertical Line

Write the equation of the line graphed in Figure 17.

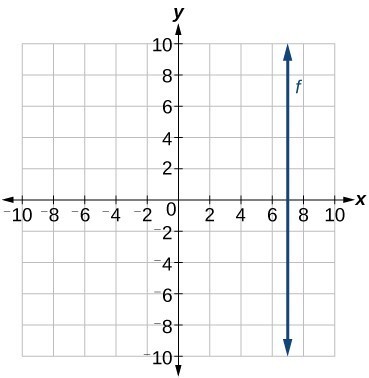
Graph of two functions where the baby blue line is y = -2/3x + 7, and the blue line is y = -x + 1.

Figure 17

Solution

The constant x-value is 7, so the equation is x = 7.