An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation [latex]2x+1=7[/latex] has the unique solution [latex]x=3[/latex] because when we substitute 3 for [latex]x[/latex] in the equation, we obtain the true statement [latex]2\left(3\right)+1=7[/latex].
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area [latex]A[/latex] of a circle in terms of the radius [latex]r[/latex] of the circle: [latex]A=\pi {r}^{2}[/latex]. For any value of [latex]r[/latex], the area [latex]A[/latex] can be found by evaluating the expression [latex]\pi {r}^{2}[/latex].
Example 11: Using a Formula
A right circular cylinder with radius [latex]r[/latex] and height [latex]h[/latex] has the surface area [latex]S[/latex] (in square units) given by the formula [latex]S=2\pi r\left(r+h\right)[/latex]. Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of [latex]\pi[/latex].
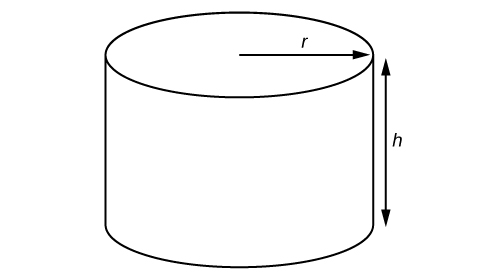
Figure 3. Right circular cylinder
Solution
Evaluate the expression [latex]2\pi r\left(r+h\right)[/latex] for [latex]r=6[/latex] and [latex]h=9[/latex].
The surface area is [latex]180\pi[/latex] square inches.
Try It 11
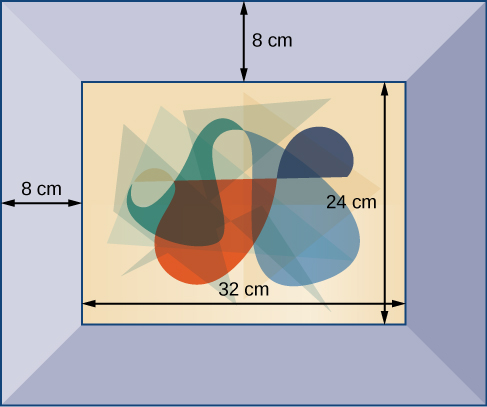
Figure 4
A photograph with length L and width W is placed in a matte of width 8 centimeters (cm). The area of the matte (in square centimeters, or cm2) is found to be [latex]A=\left(L+16\right)\left(W+16\right)-L\cdot W[/latex]. Find the area of a matte for a photograph with length 32 cm and width 24 cm.
Candela Citations
- College Algebra. Authored by: OpenStax College Algebra. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution