Draw and interpret scatter plots

A scatter plot is a graph of plotted points that may show a relationship between two sets of data. If the relationship is from a linear model, or a model that is nearly linear, the professor can draw conclusions using his knowledge of linear functions. Below is a sample scatter plot.

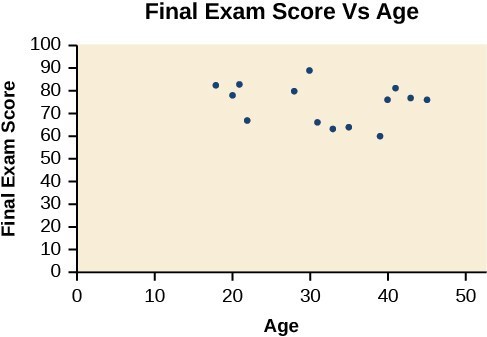
Scatter plot, titled 'Final Exam Score VS Age'. The x-axis is the age, and the y-axis is the final exam score. The range of ages are between 20s - 50s, and the range for scores are between upper 50s and 90s.

Figure 1. A scatter plot of age and final exam score variables

Notice this scatter plot does not indicate a linear relationship. The points do not appear to follow a trend. In other words, there does not appear to be a relationship between the age of the student and the score on the final exam.

Example 1: Using a Scatter Plot to Investigate Cricket Chirps

The table below shows the number of cricket chirps in 15 seconds, for several different air temperatures, in degrees Fahrenheit.[1] Plot this data, and determine whether the data appears to be linearly related.

Chirps 44 35 20.4 33 31 35 18.5 37 26
Temperature 80.5 70.5 57 66 68 72 52 73.5 53

Solution

Plotting this data suggests that there may be a trend. We can see from the trend in the data that the number of chirps increases as the temperature increases. The trend appears to be roughly linear, though certainly not perfectly so.

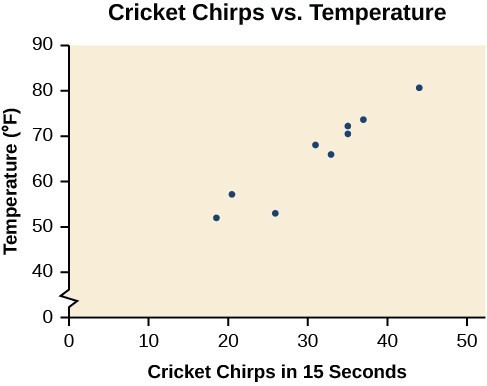
Scatter plot, titled 'Cricket Chirps Vs Air Temperature'. The x-axis is the Cricket Chirps in 15 Seconds, and the y-axis is the Temperature (F). The line regression is generally positive.

Figure 2

  1. Selected data from http://classic.globe.gov/fsl/scientistsblog/2007/10/. Retrieved Aug 3, 2010 ↵