Solutions to Try Its
1. Vertices: [latex]\left(\pm 3,0\right)[/latex]; Foci: [latex]\left(\pm \sqrt{34},0\right)[/latex]
2. [latex]\frac{{y}^{2}}{4}-\frac{{x}^{2}}{16}=1[/latex]
3. [latex]\frac{{\left(y - 3\right)}^{2}}{25}+\frac{{\left(x - 1\right)}^{2}}{144}=1[/latex]
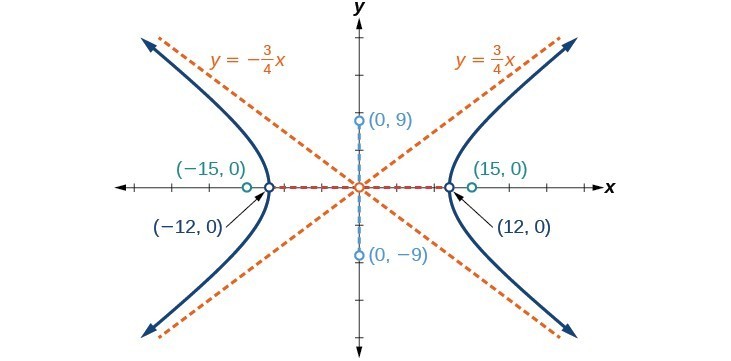
4. vertices: [latex]\left(\pm 12,0\right)[/latex]; co-vertices: [latex]\left(0,\pm 9\right)[/latex]; foci: [latex]\left(\pm 15,0\right)[/latex]; asymptotes: [latex]y=\pm \frac{3}{4}x[/latex];
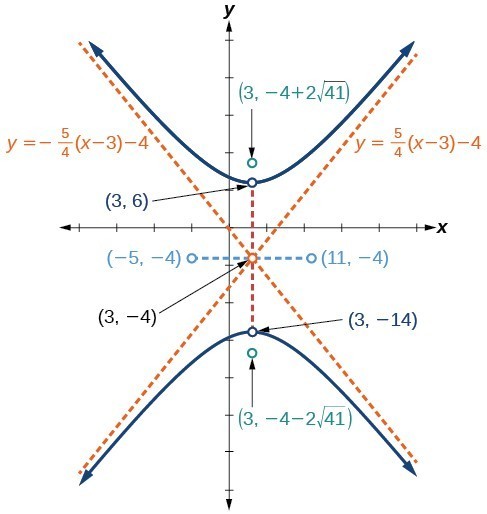
5. center: [latex]\left(3,-4\right)[/latex]; vertices: [latex]\left(3,-14\right)[/latex] and [latex]\left(3,6\right)[/latex]; co-vertices: [latex]\left(-5,-4\right)[/latex]; and [latex]\left(11,-4\right)[/latex]; foci: [latex]\left(3,-4 - 2\sqrt{41}\right)[/latex] and [latex]\left(3,-4+2\sqrt{41}\right)[/latex]; asymptotes: [latex]y=\pm \frac{5}{4}\left(x - 3\right)-4[/latex]
6. The sides of the tower can be modeled by the hyperbolic equation. [latex]\frac{{x}^{2}}{400}-\frac{{y}^{2}}{3600}=1\text{or }\frac{{x}^{2}}{{20}^{2}}-\frac{{y}^{2}}{{60}^{2}}=1[/latex].
Solutions to Odd-Numbered Exercises
1. A hyperbola is the set of points in a plane the difference of whose distances from two fixed points (foci) is a positive constant.
3. The foci must lie on the transverse axis and be in the interior of the hyperbola.
5. The center must be the midpoint of the line segment joining the foci.
7. yes [latex]\frac{{x}^{2}}{{6}^{2}}-\frac{{y}^{2}}{{3}^{2}}=1[/latex]
9. yes [latex]\frac{{x}^{2}}{{4}^{2}}-\frac{{y}^{2}}{{5}^{2}}=1[/latex]
11. [latex]\frac{{x}^{2}}{{5}^{2}}-\frac{{y}^{2}}{{6}^{2}}=1[/latex]; vertices: [latex]\left(5,0\right),\left(-5,0\right)[/latex]; foci: [latex]\left(\sqrt{61},0\right),\left(-\sqrt{61},0\right)[/latex]; asymptotes: [latex]y=\frac{6}{5}x,y=-\frac{6}{5}x[/latex]
13. [latex]\frac{{y}^{2}}{{2}^{2}}-\frac{{x}^{2}}{{9}^{2}}=1[/latex]; vertices: [latex]\left(0,2\right),\left(0,-2\right)[/latex]; foci: [latex]\left(0,\sqrt{85}\right),\left(0,-\sqrt{85}\right)[/latex]; asymptotes: [latex]y=\frac{2}{9}x,y=-\frac{2}{9}x[/latex]
15. [latex]\frac{{\left(x - 1\right)}^{2}}{{3}^{2}}-\frac{{\left(y - 2\right)}^{2}}{{4}^{2}}=1[/latex]; vertices: [latex]\left(4,2\right),\left(-2,2\right)[/latex]; foci: [latex]\left(6,2\right),\left(-4,2\right)[/latex]; asymptotes: [latex]y=\frac{4}{3}\left(x - 1\right)+2,y=-\frac{4}{3}\left(x - 1\right)+2[/latex]
17. [latex]\frac{{\left(x - 2\right)}^{2}}{{7}^{2}}-\frac{{\left(y+7\right)}^{2}}{{7}^{2}}=1[/latex]; vertices: [latex]\left(9,-7\right),\left(-5,-7\right)[/latex]; foci: [latex]\left(2+7\sqrt{2},-7\right),\left(2 - 7\sqrt{2},-7\right)[/latex]; asymptotes: [latex]y=x - 9,y=-x - 5[/latex]
19. [latex]\frac{{\left(x+3\right)}^{2}}{{3}^{2}}-\frac{{\left(y - 3\right)}^{2}}{{3}^{2}}=1[/latex]; vertices: [latex]\left(0,3\right),\left(-6,3\right)[/latex]; foci: [latex]\left(-3+3\sqrt{2},1\right),\left(-3 - 3\sqrt{2},1\right)[/latex]; asymptotes: [latex]y=x+6,y=-x[/latex]
21. [latex]\frac{{\left(y - 4\right)}^{2}}{{2}^{2}}-\frac{{\left(x - 3\right)}^{2}}{{4}^{2}}=1[/latex]; vertices: [latex]\left(3,6\right),\left(3,2\right)[/latex]; foci: [latex]\left(3,4+2\sqrt{5}\right),\left(3,4 - 2\sqrt{5}\right)[/latex]; asymptotes: [latex]y=\frac{1}{2}\left(x - 3\right)+4,y=-\frac{1}{2}\left(x - 3\right)+4[/latex]
23. [latex]\frac{{\left(y+5\right)}^{2}}{{7}^{2}}-\frac{{\left(x+1\right)}^{2}}{{70}^{2}}=1[/latex]; vertices: [latex]\left(-1,2\right),\left(-1,-12\right)[/latex]; foci: [latex]\left(-1,-5+7\sqrt{101}\right),\left(-1,-5 - 7\sqrt{101}\right)[/latex]; asymptotes: [latex]y=\frac{1}{10}\left(x+1\right)-5,y=-\frac{1}{10}\left(x+1\right)-5[/latex]
25. [latex]\frac{{\left(x+3\right)}^{2}}{{5}^{2}}-\frac{{\left(y - 4\right)}^{2}}{{2}^{2}}=1[/latex]; vertices: [latex]\left(2,4\right),\left(-8,4\right)[/latex]; foci: [latex]\left(-3+\sqrt{29},4\right),\left(-3-\sqrt{29},4\right)[/latex]; asymptotes: [latex]y=\frac{2}{5}\left(x+3\right)+4,y=-\frac{2}{5}\left(x+3\right)+4[/latex]
27. [latex]y=\frac{2}{5}\left(x - 3\right)-4,y=-\frac{2}{5}\left(x - 3\right)-4[/latex]
29. [latex]y=\frac{3}{4}\left(x - 1\right)+1,y=-\frac{3}{4}\left(x - 1\right)+1[/latex]
31.
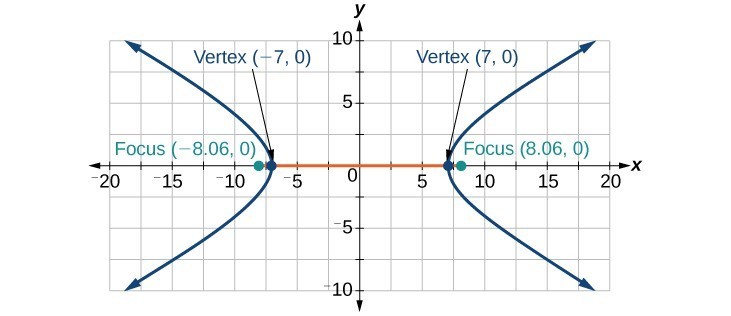
33.
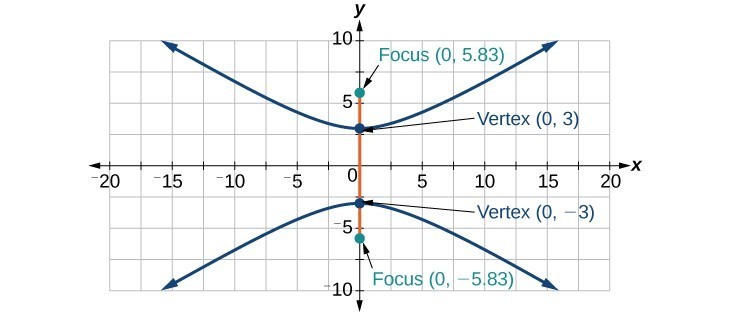
35.
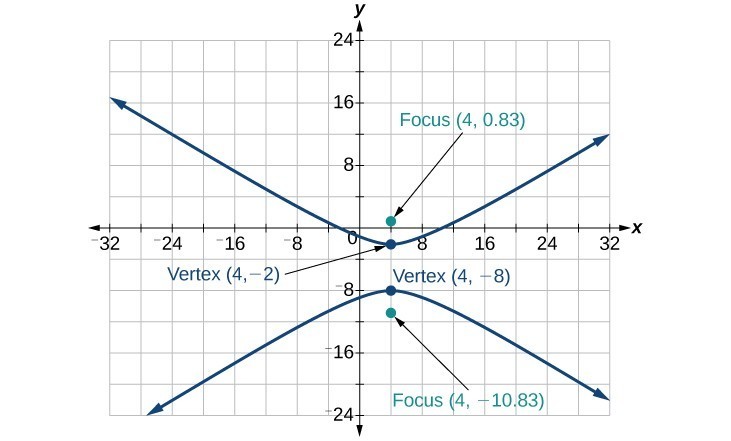
37.
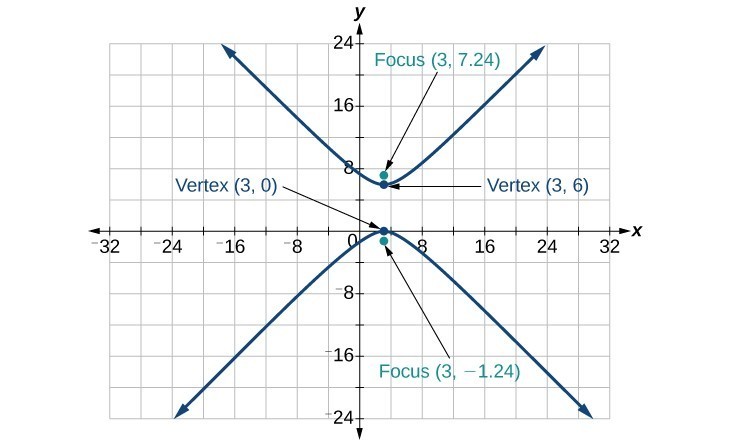
39.
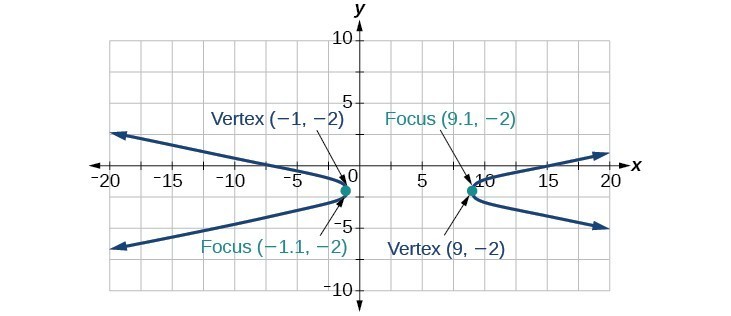
41.
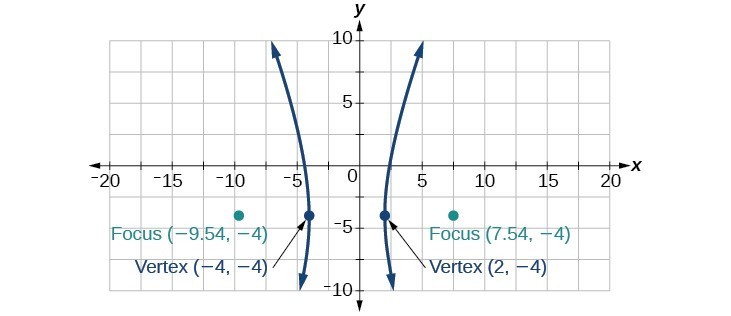
43.
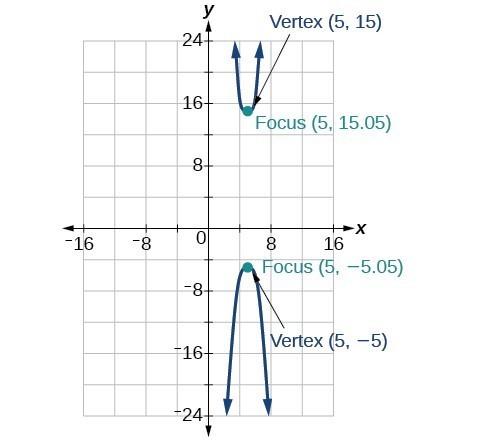
45. [latex]\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1[/latex]
47. [latex]\frac{{\left(x - 6\right)}^{2}}{25}-\frac{{\left(y - 1\right)}^{2}}{11}=1[/latex]
49. [latex]\frac{{\left(x - 4\right)}^{2}}{25}-\frac{{\left(y - 2\right)}^{2}}{1}=1[/latex]
51. [latex]\frac{{y}^{2}}{16}-\frac{{x}^{2}}{25}=1[/latex]
53. [latex]\frac{{y}^{2}}{9}-\frac{{\left(x+1\right)}^{2}}{9}=1[/latex]
55. [latex]\frac{{\left(x+3\right)}^{2}}{25}-\frac{{\left(y+3\right)}^{2}}{25}=1[/latex]
57. [latex]y\left(x\right)=3\sqrt{{x}^{2}+1},y\left(x\right)=-3\sqrt{{x}^{2}+1}[/latex]
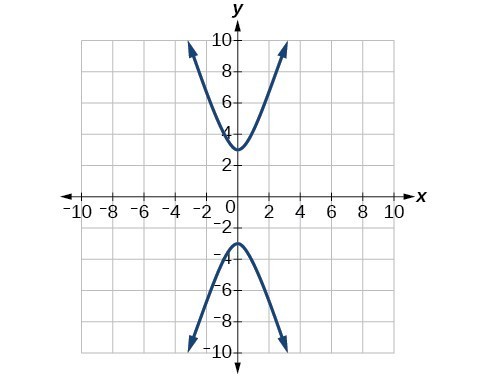
59. [latex]y\left(x\right)=1+2\sqrt{{x}^{2}+4x+5},y\left(x\right)=1 - 2\sqrt{{x}^{2}+4x+5}[/latex]
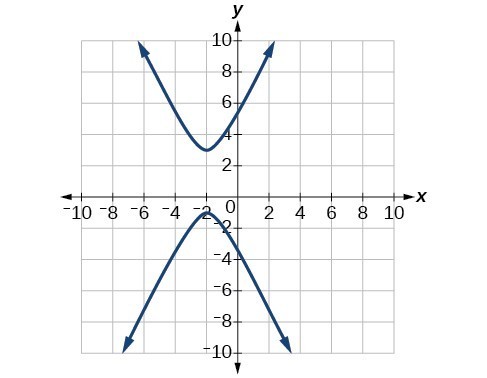
61. [latex]\frac{{x}^{2}}{25}-\frac{{y}^{2}}{25}=1[/latex]
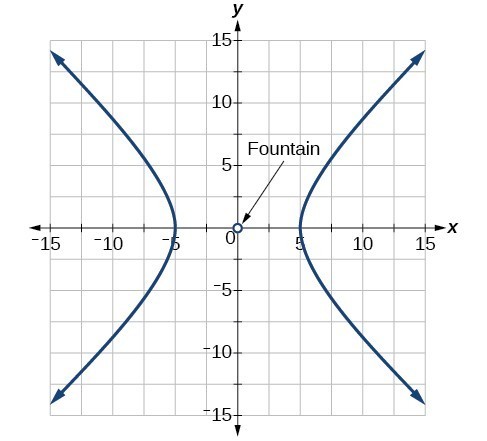
63. [latex]\frac{{x}^{2}}{100}-\frac{{y}^{2}}{25}=1[/latex]
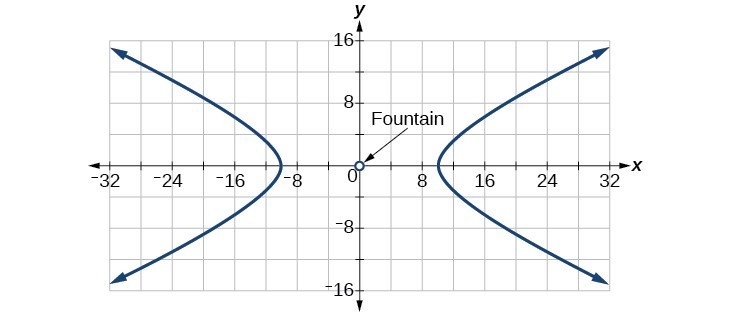
65. [latex]\frac{{x}^{2}}{400}-\frac{{y}^{2}}{225}=1[/latex]
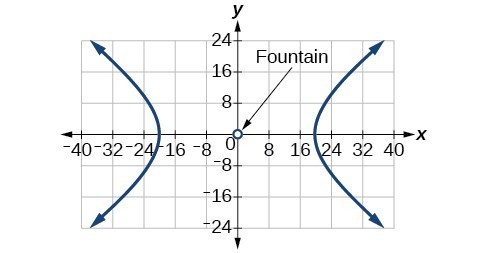
67. [latex]\frac{{\left(x - 1\right)}^{2}}{0.25}-\frac{{y}^{2}}{0.75}=1[/latex]
69. [latex]\frac{{\left(x - 3\right)}^{2}}{4}-\frac{{y}^{2}}{5}=1[/latex]
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution