Solutions

Solutions to Try Its

1. The path passes through the origin and has vertex at (−4, 7)(−4, 7), so (h)x=−716(x+4)2+7(h)x=−716(x+4)2+7. To make the shot, h(−7.5)h(−7.5) would need to be about 4 but h(−7.5)≈1.64h(−7.5)≈1.64; he doesn’t make it.

2. g(x)=x2−6x+13g(x)=x2−6x+13 in general form; g(x)=(x−3)2+4g(x)=(x−3)2+4 in standard form

3. The domain is all real numbers. The range is f(x)≥811f(x)≥811, or [811,∞)[811,∞).

4. y-intercept at (0, 13), No x-intercepts

5. a. 3 seconds  b. 256 feet  c. 7 seconds

Solutions to Odd-Numbered Exercises

1. When written in that form, the vertex can be easily identified.

3. If a=0a=0 then the function becomes a linear function.

5. If possible, we can use factoring. Otherwise, we can use the quadratic formula.

7. f(x)=(x+1)2−2f(x)=(x+1)2−2, Vertex (−1,−4)(−1,−4)

9. f(x)=(x+52)2−334f(x)=(x+52)2−334, Vertex (−52,−334)(−52,−334)

11. f(x)=3(x−1)2−12f(x)=3(x−1)2−12, Vertex (1,−12)(1,−12)

13. f(x)=3(x−56)2−3712f(x)=3(x−56)2−3712, Vertex (56,−3712)(56,−3712)

15. Minimum is −172−172 and occurs at 5252. Axis of symmetry is x=52x=52.

17. Minimum is −1716−1716 and occurs at −18−18. Axis of symmetry is x=−18x=−18.

19. Minimum is −72−72 and occurs at –3. Axis of symmetry is x=−3x=−3.

21. Domain is (−∞,∞)(−∞,∞). Range is [2,∞)[2,∞).

23. Domain is (−∞,∞)(−∞,∞). Range is [−5,∞)[−5,∞).

25. Domain is (−∞,∞)(−∞,∞). Range is [−12,∞)[−12,∞).

27. {2i√2,−2i√2}{2i√2,−2i√2}

29. {3i√3,−3i√3}{3i√3,−3i√3}

31. {2+i,2−i}{2+i,2−i}

33. {2+3i,2−3i}{2+3i,2−3i}

35. {5+i,5−i}

37. {2+2√6,2−2√6}

39. {−12+32i,−12−32i}

41. {−35+15i,−35−15i}

43. {−12+12i√7,−12−12i√7}

45. f(x)=x2−4x+4

47. f(x)=x2+1

49. f(x)=649x2+6049x+29749

51. f(x)=−x2+1

53. Vertex (1, −1), Axis of symmetry is x=1. Intercepts are (0,0),(2,0).

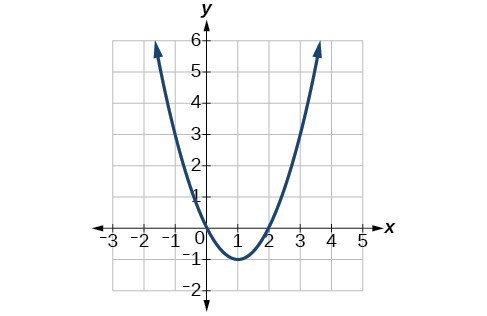
Graph of f(x) = x^2-2x

55. Vertex (52,−494), Axis of symmetry is (0,−6),(−1,0),(6,0).

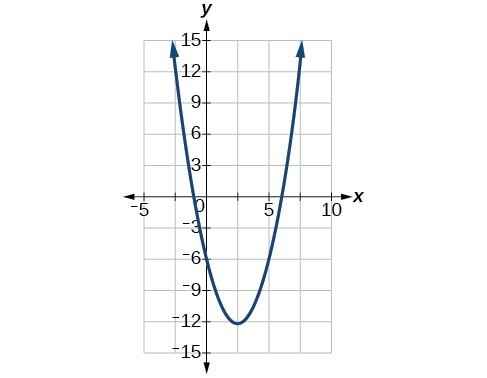
Graph of f(x)x^2-5x-6

57. Vertex (54,−398), Axis of symmetry is x=54. Intercepts are (0,−8).

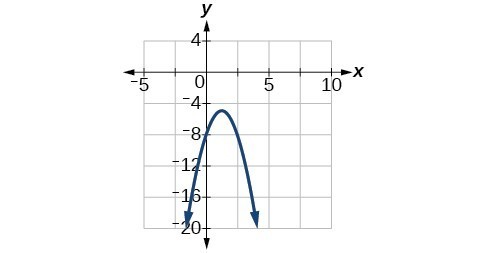
Graph of f(x)=-2x^2+5x-8

59. f(x)=x2−4x+1

61. f(x)=−2x2+8x−1

63. f(x)=12x2−3x+72

65. f(x)=x2+1

67. f(x)=2−x2

69. f(x)=2x2

71. The graph is shifted up or down (a vertical shift).

73. 50 feet

75. Domain is (−∞,∞). Range is [−2,∞).

77. Domain is (−∞,∞) Range is (−∞,11].

79. f(x)=2x2−1

81. f(x)=3x2−9

83. f(x)=5x2−77

85. 50 feet by 50 feet. Maximize f(x)=−x2+100x.

87. 125 feet by 62.5 feet. Maximize f(x)=−2x2+250x.

89. 6 and –6; product is –36; maximize f(x)=x2+12x.

91. 2909.56 meters

93. $10.70