Solutions to Try Its
1. [latex]\left\{-5,0,5,10,15\right\}\\[/latex]
2. [latex]\left(-\infty ,\infty \right)\\[/latex]
3. [latex]\left(-\infty ,\frac{1}{2}\right)\cup \left(\frac{1}{2},\infty \right)\\[/latex]
4. [latex]\left[-\frac{5}{2},\infty \right)\\[/latex]
5. values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3;
[latex]\left\{x|x\le -2\text{or}-1\le x<3\right\}\\[/latex];
[latex]\left(-\infty ,-2\right]\cup \left[-1,3\right)\\[/latex]
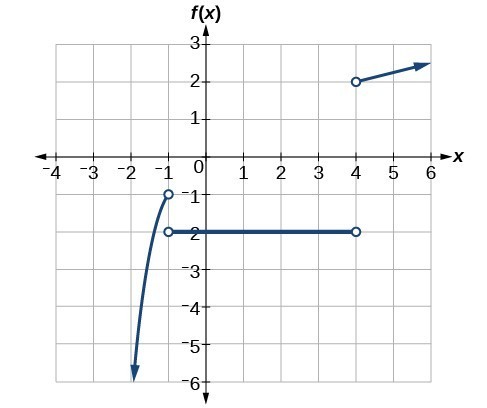
Solutions for Odd-Numbered Section Exercises
1. The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.
3. There is no restriction on [latex]x[/latex] for [latex]f\left(x\right)=\sqrt[3]{x}\\[/latex] because you can take the cube root of any real number. So the domain is all real numbers, [latex]\left(-\infty ,\infty \right)\\[/latex]. When dealing with the set of real numbers, you cannot take the square root of negative numbers. So [latex]x[/latex] -values are restricted for [latex]f\left(x\right)=\sqrt[]{x}[/latex] to nonnegative numbers and the domain is [latex]\left[0,\infty \right)\\[/latex].
5. Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the [latex]x[/latex] -axis and [latex]y[/latex] -axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate [latex]-\infty[/latex] or [latex]\text{ }\infty \\[/latex]. Combine the graphs to find the graph of the piecewise function.
7. [latex]\left(-\infty ,\infty \right)\\[/latex]
9. [latex]\left(-\infty ,3\right]\\[/latex]
11. [latex]\left(-\infty ,\infty \right)\\[/latex]
13. [latex]\left(-\infty ,\infty \right)\\[/latex]
15. [latex]\left(-\infty ,-\frac{1}{2}\right)\cup \left(-\frac{1}{2},\infty \right)\\[/latex]
17. [latex]\left(-\infty ,-11\right)\cup \left(-11,2\right)\cup \left(2,\infty \right)\\[/latex]
19. [latex]\left(-\infty ,-3\right)\cup \left(-3,5\right)\cup \left(5,\infty \right)\\[/latex]
21. [latex]\left(-\infty ,5\right)\\[/latex]
23. [latex]\left[6,\infty \right)\\[/latex]
25. [latex]\left(-\infty ,-9\right)\cup \left(-9,9\right)\cup \left(9,\infty \right)\\[/latex]
27. Domain: [latex]\left(2,8\right][/latex] Range [latex]\left[6,8\right)\\[/latex]
29. Domain: [latex]\left[-4, 4\right][/latex] Range: [latex]\left[0, 2\right]\\[/latex]
31. Domain: [latex]\left[-5,\text{ }3\right)[/latex] Range: [latex]\left[0,2\right]\\[/latex]
33. Domain: [latex]\left(-\infty ,1\right][/latex] Range: [latex]\left[0,\infty \right)\\[/latex]
35. Domain: [latex]\left[-6,-\frac{1}{6}\right]\cup \left[\frac{1}{6},6\right]\\[/latex] Range: [latex]\left[-6,-\frac{1}{6}\right]\cup \left[\frac{1}{6},6\right]\\[/latex]
37. Domain: [latex]\left[-3,\text{ }\infty \right)\\[/latex] Range: [latex]\left[0,\infty \right)\\[/latex]
39. Domain: [latex]\left(-\infty ,\infty \right)\\[/latex]

41. Domain: [latex]\left(-\infty ,\infty \right)\\[/latex]

43. Domain: [latex]\left(-\infty ,\infty \right)\\[/latex]

45. Domain: [latex]\left(-\infty ,\infty \right)\\[/latex]

47. [latex]\begin{cases}f\left(-3\right)=1;& f\left(-2\right)=0;& f\left(-1\right)=0;& f\left(0\right)=0\end{cases}\\[/latex]
49. [latex]\begin{cases}f\left(-1\right)=-4;& f\left(0\right)=6;& f\left(2\right)=20;& f\left(4\right)=34\end{cases}\\[/latex]
51. [latex]\begin{cases}f\left(-1\right)=-5;& f\left(0\right)=3;& f\left(2\right)=3;& f\left(4\right)=16\end{cases}\\[/latex]
53. Domain: [latex]\left(-\infty ,1\right)\cup \left(1,\infty \right)\\[/latex]
55. Window: [latex]\left[-0.5,-0.1\right][/latex] Range: [latex]\left[4,\text{ }100\right]\\[/latex]
![Graph of the equation from [0.1, 0.5].](https://s3-us-west-2.amazonaws.com/courses-images-archive-read-only/wp-content/uploads/sites/924/2015/11/25200709/CNX_Precalc_Figure_01_02_222.jpg)
Window: [latex]\left[0.1,\text{ }0.5\right][/latex] Range: [latex]\left[4,\text{ }100\right][/latex]
![Graph of the equation from [0.1, 0.5].](https://s3-us-west-2.amazonaws.com/courses-images-archive-read-only/wp-content/uploads/sites/924/2015/11/25200709/CNX_Precalc_Figure_01_02_222.jpg)
57. [latex]\left[0,\text{ }8\right]\\[/latex]
59. Many answers. One function is [latex]f\left(x\right)=\frac{1}{\sqrt{x - 2}}\\[/latex].
61. The domain is [latex]\left[0,\text{ }6\right][/latex]; it takes 6 seconds for the projectile to leave the ground and return to the ground.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.