Functions are a correspondence between two sets, called the domain and the range. When defining a function, you usually state what kind of numbers the domain (x) and range (f(x)) values can be. But even if you say they are real numbers, that doesn’t mean that all real numbers can be used for x. It also doesn’t mean that all real numbers can be function values, f(x). There may be restrictions on the domain and range. The restrictions partly depend on the type of function.

In this topic, all functions will be restricted to real number values. That is, only real numbers can be used in the domain, and only real numbers can be in the range.

There are two main reasons why domains are restricted.

• You can’t divide by 0.
• You can’t take the square (or other even) root of a negative number, as the result will not be a real number.

Find Domain and Range From a Graph

Finding domain and range of different functions is often a matter of asking yourself, what values can this function not have? Pictures make it easier to visualize what domain and range are, so we will show how to define the domain and range of functions given their graphs.

What are the domain and range of the real-valued function [latex]f(x)=x+3[/latex]?
This is a linear function. Remember that linear functions are lines that continue forever in each direction.

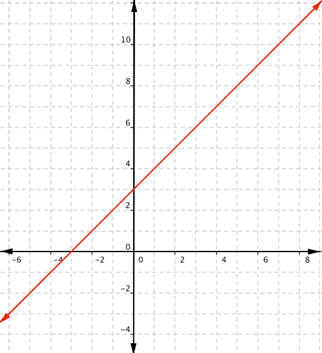
Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range.
The domain and range are all real numbers.

For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.

Example

What are the domain and range of the real-valued function [latex]f(x)=−3x^{2}+6x+1[/latex]?

Show Solution

This is a quadratic function. There are no rational (divide by zero) or radical (negative number under a root) expressions, so there is nothing that will restrict the domain. Any real number can be used for x to get a meaningful output.

Because the coefficient of [latex]x^{2}[/latex] is negative, it will open downward. With quadratic functions, remember that there is either a maximum (greatest) value, or a minimum (least) value. In this case, there is a maximum value.

The vertex, or high point, is at (1, 4). From the graph, you can see that [latex]f(x)\leq4[/latex].

Answer

The domain is all real numbers, and the range is all real numbers f(x) such that [latex]f(x)\leq4[/latex].

You can check that the vertex is indeed at (1, 4). Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value. The vertex must lie on the line of reflection, because it’s the only point that does not have a mirror image!

In the previous example, notice that when [latex]x=2[/latex] and when [latex]x=0[/latex], the function value is 1. (You can verify this by evaluating f(2) and f(0).) That is, both (2, 1) and (0, 1) are on the graph. The line of reflection here is [latex]x=1[/latex], so the vertex must be at the point (1, f(1)). Evaluating f(1) gives [latex]f(1)=4[/latex], so the vertex is at (1, 4).

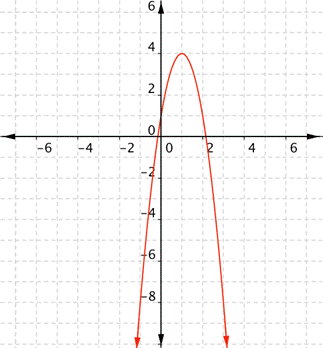
Example

What is the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}[/latex]?

Show Solution

This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means [latex]x+5\geq0[/latex], so [latex]x\geq−5[/latex].

Since the square root must always be positive or 0, [latex] \displaystyle \sqrt{x+5}\ge 0[/latex]. That means [latex] \displaystyle -2+\sqrt{x+5}\ge -2[/latex].

Answer

The domain is all real numbers x where [latex]x\geq−5[/latex], and the range is all real numbers f(x) such that [latex]f(x)\geq−2[/latex].

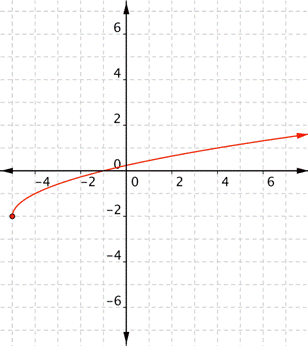
Division by 0 could happen whenever the function has a variable in the denominator of a rational expression. That is, it’s something to look for in rational functions. Look at these examples, and note that “division by 0” doesn’t necessarily mean that x is 0! The following is an example of rational function, w will cover these in detail later.

Example

What is the domain of the real-valued function [latex] \displaystyle f(x)=\frac{3x}{x+2}[/latex]?

Show Solution

This is a rational function. The domain of a rational function is restricted where the denominator is 0. In this case, [latex]x+2[/latex] is the denominator, and this is 0 only when [latex]x=−2[/latex].

Answer

The domain is all real numbers except [latex]−2[/latex]

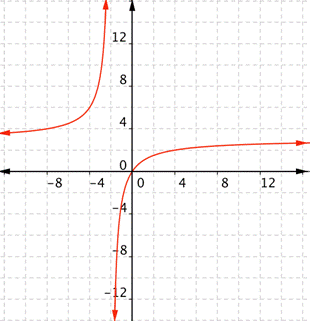
In the following video we show how to define the domain and range of functions from their graphs.

Example: Finding Domain and Range from a Graph

Find the domain and range of the function [latex]f[/latex].

Solution

We can observe that the horizontal extent of the graph is –3 to 1, so the domain of [latex]f[/latex] is [latex]\left(-3,1\right][/latex].

The vertical extent of the graph is 0 to [latex]–4[/latex], so the range is [latex]\left[-4,0\right)[/latex].

Example: Finding Domain and Range from a Graph of Oil Production

Find the domain and range of the function [latex]f[/latex].

(credit: modification of work by the U.S. Energy Information Administration)

Solution

The input quantity along the horizontal axis is “years,” which we represent with the variable [latex]t[/latex] for time. The output quantity is “thousands of barrels of oil per day,” which we represent with the variable [latex]b[/latex] for barrels. The graph may continue to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain as [latex]1973\le t\le 2008[/latex] and the range as approximately [latex]180\le b\le 2010[/latex].

In interval notation, the domain is [1973, 2008], and the range is about [180, 2010]. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.

Try It

Given the graph, identify the domain and range using interval notation.

Solution

Domain = [1950, 2002]   Range = [47,000,000, 89,000,000]

Identify a One-to-One Function

Remember that in a function, the input value must have one and only one value for the output. There is a name for the set of input values and another name for the set of output values for a function. The set of input values is called the domain of the function. And the set of output values is called the range of the function.

In the first example we remind you how to define domain and range using a table of values.

In the following video we show another example of finding domain and range from tabular data.

Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.

However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.

This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.

To visualize this concept, let’s look again at the two simple functions sketched in (a)and (b) of Figure 10.

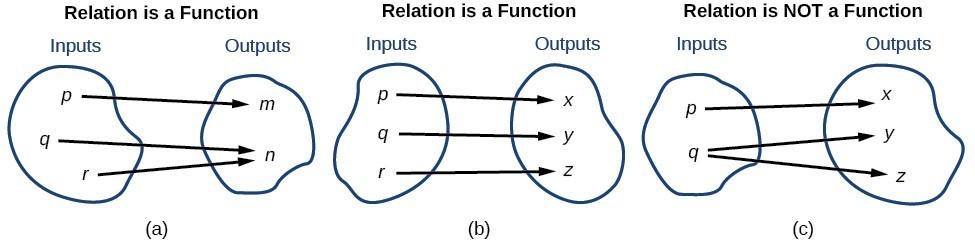
Figure 10

The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.

In the following video, we show an example of using tables of values to determine whether a function is one-to-one.

Using the Horizontal Line Test

An easy way to determine whether a function is a one-to-one function is to use the horizontal line test on the graph of the function.  To do this, draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.

Exercises

For the following graphs, determine which represent one-to-one functions.

Show Answer

The function in (a) is not one-to-one. Using the horizontal line test, as shown below, it intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)

The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.

The function (c) is not one-to-one, and is in fact not a function.

The following video provides another example of using the horizontal line test to determine whether a graph represents a one-to-one function.

Summary

In real life and in algebra, different variables are often linked. When a change in value of one variable causes a change in the value of another variable, their interaction is called a relation. A relation has an input value which corresponds to an output value. When each input value has one and only one output value, that relation is a function. Functions can be written as ordered pairs, tables, or graphs. The set of input values is called the domain, and the set of output values is called the range.